46. Параметры цилиндрических косозубых колес

В косозубых цилиндрических колесах в отличие от прямозубых оси зубьев составляют некоторый угол ? с осью колеса . Величину этого угла рекомендуют выбирать равным 10, 12, 16 и 20°. Работать в паре могут колеса только с равными углами наклона зубьев, но с разным (правое и левое) направлением винтовых линий. Оси косозубых колес параллельны.Косозубые передачи обладают рядом достоинств по сравнению с прямозубыми: благодаря наличию угла наклона ? зубья вступают в зацепление по своей длине b постепенно, что обеспечивает более равномерную и плавную работу, и, естественно, снижение шума механизма вследствие большего коэффициента перекрытия. У косозубых колес минимальное число зубьев z_k min, при котором не происходит подрезания, меньше, чем у прямозубых (z_k min = z_mincos³?). Косозубые передачи позволяют подобрать при заданном межосевом расстоянии за счет изменения угла наклона ? пару колес со стандартным модулем.К недостаткам косозубых передач следует отнести более сложное изготовление колес по сравнению с прямозубыми и появление дополнительного осевого усилия, передаваемого на опоры. Для устранения осевого усилия можно применять шевронные зубчатые колеса. Венец шевронного колеса состоит из участков с правым и левым направлением зубьев. Зубья такого колеса могут быть нарезаны на одном ободе или венец состоит из жесткого соединения двух косозубых колес с разным направлением наклона зубьев. Шевронные колеса сложнее в изготовлении косозубых.

Различают торцовое сечение в плоскости t-t вращения колеса и нормальное n-n - в плоскости, перпендикулярной направлению зуба. Параметры, определяющие размеры косозубых колес в обоих сечениях, не одинаковы, поэтому им присваивают разные индексы: параметрам в торцовом сечении - t, в нормальном - n. Окружной шаг АС (см. рис. 1) в торцовом сечении p_t = ?m_t, а в нормальном сечении шаг АВ равен p_n = ?m_n, где m_t и m_n - торцовый и нормальный модули. Из АВС следует, что p_t = p_n/cos?, поэтому

m_t = m_n/cos?. (1)

При нарезании косозубых колес ось инструмента наклоняют по отношению к оси колеса на угол ?. Стандартным является нормальный модуль m_n, и размеры профилей зуба в нормальном сечении (p_n = ?m_n; h_a = m_n; h_f = (1 + + c*)m_n; h = (2 + c*)m_n; S = ?m_n/2). Модуль m_t в торцовой плоскости, окружной шаг p_t, диаметр делительной (базовой) окружности d = m_tz косозубого колеса зависят от угла ? наклона продольных осей зубьев. Размеры косозубого колеса через стандартный модуль следующие: делительный диаметр d = (m_nz)/cos?; диаметр выступов зубьев d_a = d + 2m_n; диаметр впадин d_f = d - (2 + 2c*)m_n; длина зуба b = (3 … 15)m_n; ширина венца колеса b' = bcos?. Отметим, что ширина венца колеса влияет на величину коэффициента перекрытия, как и угол наклона ? зуба.

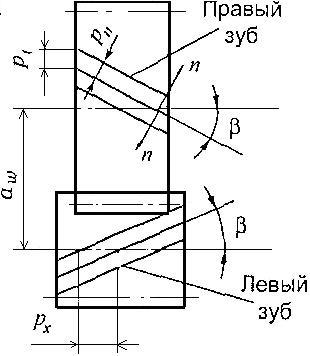
47. Силы в зацеплении косозубых цилиндрических передач

Силы в зацеплении определяют в полюсе зацепления. Сила , действующая на зуб косозубого колеса рис. 2.3.16, направлена по нормали к профилю зуба, т.е. по линии зацепления эквивалентного прямозубого колеса и составляет уголс касательной к эллипсу.

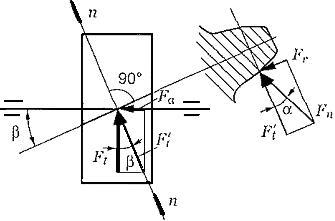Разложим эту силу на две составляющие: окружную силу на эквивалентном колесе:(2.3.22) радиальную силу на этом колесе:(2.3.33) Переходя от эквивалентного к косозубому колесу, заметим, что силаявляется радиальной силойи для этого колеса, т.е.сила Ft расположена в плоскости, касательной к начальному цилиндру, и составляет уголс осью колеса. Разложим силу Ft на две составляющие: окружную силу(2.3.35), и осевую силу(2.3.36). Окружная сила известна. 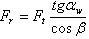Её определяют по передаваемому моменту и диаметру делительной окружности зубчатого колеса(2.3.37) Тогда из формулы (2.3.35):следуетПодставив силуи выражения,окончательно получим: радиальную силу(2.3.38) и осевую силуНа зубья шестерни и колеса действуют одинаковые, но противоположно направленные силы. При определении их направления учитывают направление вращения колёс и направление наклона линии зубьев(правое и левое).