физ / МКТ и термодинамика
.pdf
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
31 |
12 Закон Бойля – Мариотта: |
|
|
|
|
|
|
T const,m const, |
|||||||||||
|
|
PV cons при |
||||||||||||||||
|
P1V1 P2V2 |
- |
для двух состояний газа. |
|||||||||||||||
Закон Гей-Люссака: |
|
|
|
|
|
|
|
|||||||||||
|
V |
|
|
const при |
P const,m const , |
|||||||||||||
|
|
|
||||||||||||||||
|
T |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
V1 |
|
|
V2 |
|
|
- для двух состояний газа. |
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
T |
|
T |
2 |
|
|
||||||||
1 |
|
|
|
|
|
|
|
|
|
|
||||||||
Закон Шарля: |
|
|
|
|
|
|
|
|||||||||||
|
|
P |
cons |
при |
T const,m const , |
|||||||||||||
|
|
|
|
|
||||||||||||||
|
|
T |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
P1 |
|
P2 |
|
- для двух состояний газа. |
||||||||
|
|
|
|
|
|
|
|
T |
||||||||||
|
|
|
T |
|
||||||||||||||
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|||||||
Объединенный газовый закон |
|
|
||||||||||||||||
|
|
|
|
|
|
|
PV |
const при m const , |
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
P1V1 |
|
P2V2 |
- двух состояний газа. |
|||||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
T1 |
|
|
T2 |
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||
13 Уравнение Клапейрона-Менделеева (уравнение состояния идеального газа)
PV m RT ,
где R – универсальная газовая постоянная, ? – молярная масса газа.
14 Закон Дальтона. Давление Р смеси различных газов равно сумме парциальных давлений Рi газов, составляющих смесь:
n
P P1 P2 ... Pn Pi .
i 1
Закон Авогадро. Масса и размер молекул
2.1На изделие с площадью поверхности S = 10 см2 нанесен слой золота толщиной h = 0,5 мкм. Сколько атомов золота N содержится в покрытии?
Молярная масса золота M = 0,197 кг/моль, его плотность = 19,3 103 кг/м3. (3 1019)
32
2.2Определить число N атомов в 1 кг водорода и массу m0 одного атома
водорода. |
(3,01 1026; 3,32 10-27 кг) |
2.3Плотность данного вещества , его молярная масса М. Сколько молекул N содержится в единице массы этого вещества? В единице объема?
2.4Допустимая концентрация молекул в парах ртути в воздухе n = 3 1016м-3. При какой массе m паров ртути в комнате объемом V = 40 м3 наступает
опасность отравления? Молярная масса ртути М = 0, 201 кг/м3. |
(4 10-7 кг) |
2.5За какое время t полностью испарится вода из стакана объемом V = 200 см3,
если налита четверть стакана и при этом за каждую t1 = 1с с поверхности
воды вылетает N1 = 5 1020 молекул? Плотность воды |
= |
1 103 кг/м3, ее |
молярная масса М = 0,018 кг/моль. |
|
(3,3 103 с) |
2.6В стакан с водой объемом V = 200 см3 бросили крупинку поваренной соли
массой m = 5 мг. Сколько молекул соли N1 окажется в одной капле раствора объемом V1 = 1 мм3, если соль, растворившись, распределилась по стакану равномерно? Молярная масса поваренной соли М = 0,058 кг/моль. (2,6 1014)
2.7Сколько N раз можно было бы опоясать Землю по экватору цепочкой из молекул воды, содержащихся в одном стакане объемом V = 200 см3. Диаметр молекулы воды D = 8 10-10 м, радиус земного шара R = 6400 км. Плотность воды = 1 103 кг/м3, ее молярная масса М = 0,018 кг/моль. (1 108)
2.8Оцените минимальное расстояние d между центрами соседних атомов
железа, считая его кристаллическую решетку кубической. |
(230 пм) |
2.9Известно, что нельзя заставить капельку нефти объемом 1 мм3 расплыться
по поверхности воды так, чтобы она заняла площадь больше 3 м2. Оцените
по этим данным |
минимальные размеры d частиц нефти. М = 1 кг/моль, |
|
= 0,8 103 кг/м3. |
|
(3,3 10-10 м) |
2.10 В герметично |
закрытом |
сосуде помещена крупинка радиоактивного |
вещества радия, испускающего альфа-частицы, представляющие собой ядра |
||
гелия. При нормальных условиях за t = 1 году в сосуде накопилось V = |
||
1,56 10-7 м3 газообразного |
гелия. Сколько частиц N испускает радий за t1 = |
|
1 c? При нормальных условиях объем моля любого газа Vмоль = 22,4 л.
(1 1011)
Основное уравнение молекулярно-кинетической теории идеальных газов. Скорости молекул. Средняя кинетическая энергия поступательного
движения молекул идеального газа
2.11Вычислить средний квадрат скорости < >2 движения молекул газа, если его масса m = 6 кг, объем V = 4,9 м3 и давление Р = 200 кПа. (4,9 105 м2/с2)
2.12В результате нагревания давление газа увеличилось вдвое, а его плотность –
вполтора раза. Во сколько раз увеличилась при этом средняя квадратичная
скорость молекул газа? |
(в 1,15 раза) |
33
2.13Во сколько раз изменится давление газа, если его объем уменьшить в два раза, а среднюю кинетическую энергию увеличить в 5 раз? Газ находится в
закрытом сосуде с резиновыми стенками. |
(в 10 раз) |
2.14Найти концентрацию n и плотность газа, оказывающего давление Р = 200 кПа при средней квадратичной скорость его молекул < кв> = 300 м/с.
Молярная масса газа М = 0,029 кг/моль (воздух). |
(1,4 1026 м-3; 6,7 кг/м3) |
2.15Во сколько раз средняя квадратичная скорость молекулы водорода больше средней квадратичной скорости молекулы кислорода, если температуры
|
этих газов одинаковы? Молярные массы этих газов определить по таблице |
|
|
Менделеева. |
(в 4 раза) |
2.16 |
Насколько средняя квадратичная скорость молекул воздуха летом при t1 = |
|
|
27 0C больше их средней квадратичной скорости зимой при t2 = -17 0C ? |
|
|
Молярная масса воздуха М = 0,029 кг/моль. |
(38 м/с) |
2.17 |
Какова наиболее вероятная скорость υВ молекул водорода при температуре |
|
|
Т = 400 К? |
(1,82 км/с) |
2.18 |
Определите наиболее вероятную скорость В молекул газа, плотность |
|
|
которого при давлении Р = 40 кПа составляет = 0,35 кг/м3. |
(478 м/с) |
2.19Определить среднюю арифметическую скорость <υ> молекул газа, если известно, что их средняя квадратичная скорость <υкв> = 1 км/с.
|
(0,92 км/с) |
2.20 Определить среднюю арифметическую |
скорость <υ> молекул азота при |
27 0С. |
(476 м/с) |
2.21Современная техника позволяет создать вакуум, при котором давление
оставшегося газа не превышает Р = 0,1 нПа. Сколько молекул газа N останется в сосуде объемом 1 см3 при таком вакууме и какова средняя
кинетическая энергия 0 этих молекул? Температура газа 300 К.
(6,2 10-21 Дж)
2.22В баллоне емкостью V = 3 л содержится = 0,1 моль идеального газа под давлением 0,2 Мпа. Чему равна средняя кинетическая энергия <Ек>
поступательного движения его молекул? |
(1,5 10-20 Дж) |
2.23Определите среднюю кинетическую энергию 0 поступательного движения молекул газа, находящегося под давлением Р = 0,1 Па. Концентрация
молекул газа равна n = 1013 см-3. |
(1,5 10-20 Дж) |
2.24Энергия поступательного движения, которой обладают все молекулы газа, находящегося в объеме 0,02 м3 при 17 0С, составляет 0,66 Дж. Найти
концентрацию молекул этого газа. |
(5,5 1015 см-3) |
Барометрическая формула
2.25 На какой высоте h давление воздуха составляет 60% от давления на уровне моря? Считать, что температура воздуха везде одинакова и равна t = 10 0С.
(4,22 км)
34
2.26Определите отношение давления воздуха на высоте 1 км к давлению на дне скважины глубиной 1 км. Воздух у поверхности Земли находится при
нормальных условиях, и его температура не зависит от высоты. |
(0,778) |
2.27Космические аппараты «Венера-5» и «Венера-6» разрушились в атмосфере Венеры на высоте 17 км от поверхности планеты. Оцените давление
венерианской атмосферы Р в момент разрушения, если у поверхности Венеры оно приблизительно равно 107 Па. Температуру считать одинаковой на всех высотах и равной 477 0С. Ускорение свободного падения на Венере 8,85 м/с2. Атмосфера Венеры состоит в основном из углекислого газа.
(3,5 106 Па)
2.28Какую массу имеет воздух, взятый в объеме 1м3: а) у поверхности Земли; б) на высоте 4 км от поверхности Земли? Температура воздуха 0 0С и не зависит от высоты. Давление у поверхности Земли Р0 = 105 Па.
(1,278 кг; 0,772 кг)
2.29Определите вес цилиндрического столба воздуха, площадь основания которого S = 1 м2 , а высота равна Останкинской телебашне (h = 530 м). Считайте, что температура воздуха T =300 К, давление у поверхности Земли
|
P0 = 105 Па. |
(6000 Н) |
|
Явления переноса |
|
2.30 |
Одним из компонентов топлива в двигателе ракеты является жидкий |
|
|
водород, плотность которого в момент закипания ρ = 7 кг/м3. Определить |
|
|
среднюю длину свободного пробега молекул водорода |
l , если |
|
эффективный диаметр молекулы водорода dэф = 0,23 нм. Газ считать |
|
|
идеальным. |
(2·10-9 м) |
2.31 |
В сосуде находится кислород при нормальных условиях. Найти среднее |
|
|
число столкновений молекул z в этом объеме за время t = 2 c. |
|
2.32 |
Эффективный диаметр молекулы кислорода dэф = 0,27 нм. |
(7·109) |
При каком давлении средняя длина свободного пробега молекул водорода |
||
|
l равна 2,5 см, если температура газа t = 67 0C ? Диаметр молекулы |
|
|
водорода принять равным d = 0,28 нм. |
(0,539 Па) |
2.33Средняя длина свободного пробега l1 молекул водорода при нормальных условиях составляет 0,1 мкм. Определить среднюю длину их свободного
|
пробега l2 при давлении Р = 0,1 мПа, если температура газа остается |
|
|
постоянной. |
(101 м) |
2.34 |
Определить: 1) плотность воздуха в сосуде; 2) концентрацию n его |
|
|
молекул; 3) среднюю длину свободного пробега l молекул, если сосуд |
|
|
откачан до давления 0,13 Па. Диаметр молекул воздуха принять равным |
|
|
0,27 нм. Температура воздуха Т = 300 К. |
(1,51 10-6 кг/м3; 3,14 1019 м-3; 0,1 м) |
2.35 |
Найдите теплопроводность водорода, если вязкость η для него при этих |
|
|
условиях равна 8,6 10-5 Па с. |
(8,93 10-4 Вт/(м К)) |
35
2.36Определить коэффициент теплопроводности λ азота, находящегося в некотором объеме при температуре 280 К. Эффективный диаметр молекул
2.37 |
азота принять равным dэф = 0,38 нм. |
|
|
(8,25 мВт/(м·К)) |
|||
Пространство между двумя параллельными пластинами площадью 150 см2 |
|||||||
|
каждая, находящимися на расстоянии 5 мм друг от друга, заполнено |
||||||
|
кислородом. Одна пластина поддерживается при температуре 17 0С, другая |
||||||
|
– при температуре 27 0С. Определите количество |
теплоты Q, |
прошедшее |
||||
|
за 5 мин посредством теплопроводности от одной пластины к другой. |
||||||
|
Кислород находится при нормальных условиях. Эффективный диаметр |
||||||
|
молекул кислорода считать равным 0,36 нм. |
|
|
(76,4 Дж) |
|||
2.38 |
Определить массу m азота, прошедшего вследствие диффузии через площад- |
||||||
|
ку 50 см2 за 20 с, если градиент плотности в направлении, |
||||||
|
перпендикулярном площадке, равен 1 кг/м4. Температура азота 290 К, а |
||||||
|
средняя длина свободного пробега его молекул равна 1 мкм. |
(15,6 мг) |
|||||
2.39 |
Определить, во сколько раз отличаются коэффициенты динамической |
||||||
|
вязкости η углекислого газа и азота, если оба газа находятся при |
||||||
|
одинаковых температуре и давлении. Эффективные диаметры молекул этих |
||||||
|
газов считать равными. |
|
|
|
(в 1.25 раз) |
||
2.40 |
Азот находится под давлением Р = 100 кПа при |
температуре |
Т = 290 К. |
||||
|
Определить коэффициенты диффузии D и внутреннего трения |
. |
|||||
|
Эффективный диаметр молекул азота принять равным 0,38 нм. |
|
|
||||
|
|
|
(9,74 10-6 м2/с; 1,13 10-5 кг/(м с)) |
||||
2.41 |
Коэффициент диффузии и внутреннего трения при некоторых условиях |
||||||
|
равны соответственно 1,42 10-4 м2/c |
и 8,5 10-6 |
Па с. Определить |
||||
|
концентрацию молекул n воздуха при этих условиях. |
(1,25·1024 м-3) |
|||||
2.42 |
Коэффициент |
диффузии и вязкость кислорода равны соответственно |
|||||
|
1,2 10-5 м2/c и |
1,95 10-5 Па с. Найдите при этих условиях: 1) |
плотность |
||||
|
кислорода; 2) длину свободного пробега l ; 3) среднюю скорость |
|
|||||
|
молекул. |
|
(1,625 кг/м3; 87 нм; 414 м/с) |
||||
Законы идеальных газов
2.43Плотность углекислотной (СО2) атмосферы Венеры примерно в 50 раз выше плотности земной атмосферы при нормальных условиях. Считая, что температура у поверхности Венеры 477 0С, найдите венерианское
атмосферное давление Р. |
(9 106 Па) |
2.44 При изотермическом сжатии газа его объем уменьшился в 3 раза, а давление
повысилось на Р = 2 атм. Чему равны давления газа Р1 |
в начале и |
Р2 в |
конце процесса? |
(1 атм; 3 |
атм) |
2.45Продукты сгорания газа охлаждаются в газоходе с 1000 0С до 300 0С. Определить во сколько раз уменьшится их объем при этом, если считать, что процесс охлаждения продуктов сгорания газа происходит при
неизменном давлении. |
(в 0,45 раз) |
|
36 |
|
2.46 Азот массой 7 |
г находится под давлением Р = 0,1 МПа и температуре |
|
Т1 = 290 К. Вследствие изобарного нагревания азот занял объем |
V2 = 10 л. |
|
Определите: 1) |
объем V1 газа до расширения; 2) температуру Т2 газа после |
|
расширения; 3) |
плотность газа до и после расширения. |
|
|
(6,02 10-3 м3; 481 К; 1,16 кг/м3; |
0,7 кг/м3) |
2.47Газ, занимающий при температуре 127 0С и давлении 100 кПа объем 2 л,
изотермически сжимают, а затем изобарно охлаждают до температуры -73 0С, после чего изотермически изменяют объем до 1 л. Найти конечное
давление Р. |
(0,1 МПа) |
2.48В начале сжатия температура газа в цилиндре двигателя внутреннего сгорания t1 = 57 0С. Найти температуру Т2 в конце сжатия, если при этом
давление возрастает в 40 раз, а объем газа уменьшается в 5 раз. |
(2640 К) |
2.49В баллоне вместимостью 15 л находится азот под давлением 100 кПа при
температуре t1 = 27 0С. После того как из баллона выпустили азот массой 14 г, температура газа стала равной t2 = 17 0C. Определите давление Р азота,
оставшегося в баллоне. |
(1 6,3 кПа) |
2.50При уменьшении объема идеального газа в три раза его давление увеличилось на 100 кПа, а абсолютная температура повысилась на 20 %.
Чему равно давление Р1 в начале процесса? (38 кПа) 2.51 В сосуде вместимостью 5 л при нормальных условиях находится азот.
Определите: 1) количество вещества ; |
2) массу m азота; 3) концентрацию |
n его молекул в сосуде. |
(0,233 моль; 6,24 г; 2,69 1025 м-3) |
2.52Два баллона с газом объемами V1 и V2 соединяют трубкой, объемом которой можно пренебречь. Насколько изменится давление в каждом баллоне, если до соединения оно было соответственно равно Р1 и Р2? Процесс
изотермический. |
( P |
P1V2 |
P2V2 |
, |
P |
P2V1 |
P1V1 |
) |
|
|
|
|
|||||
|
1 |
V1 |
V2 |
2 |
V1 |
V2 |
||
|
|
|
||||||
2.53 Сосуд содержит воздух при атмосферном давлении и температуре 20 0С. До какой температуры t нужно нагреть этот сосуд, чтобы из него вытеснилась
одна пятая часть всех молекул, первоначально находившихся в сосуде?
(93 0С)
2.54Из баллона объемом 200 дм3, содержащего гелий при давлении 2 МПа и
температуре 273 К, израсходовали часть газа, занявшего при нормальных условиях объем 1 м3. При повторном измерении давления в баллоне получено значение 1,4 МПа. При какой температуре t проведено это
измерение? |
( - 17 0С) |
2.55Баллон вместимостью V = 20 л содержит смесь водорода и азота при температуре Т = 290 К и давлении Р = 1 МПа. Определите массу m1
водорода, если масса смеси равна 150 г. |
(6,3 г) |
2.56В закрытом сосуде вместимостью 20 л находятся водород массой m1 = 6 г и гелий m2 = 12 г. Определите: 1) давление Р; 2) молярную массу М газовой смеси в сосуде, если температура смеси Т = 300 К.
(0,75 МПа; 3 10-3 кг/моль)
37
2.57 В баллоне вместимостью 0,5 дм3 содержится смесь газов, состоящая из 1020 молекул кислорода, 4 1020 молекул азота и 3,3 1020 молекул аргона. Определить: а) давление смеси Р; б) молярную массу М смеси. Температура смеси 127 0С. (9,16 103 Па; 0,033 кг/моль)
2.58Сухой атмосферный воздух содержит 23,1% кислорода (от общей массы), 75,8% азота и 1,3% аргона. Доля остальных газов пренебрежимо мала.
Определите молярную массу М воздуха и парциальные давления составляющих его газов, если атмосферное давление 105 Па.
|
(0,029 кг/моль; 2,1 104 Па, 7,8 104 Па, 9,4 102 Па) |
|
2.59 |
Чему равна плотность смеси газов , состоящая |
из кислорода массой |
|
m1 = 5 г, азота массой m2 = 4 г и гелия массой m3 = 10 г, при нормальных |
|
|
условиях? |
( 0,3 кг/м3) |
2.60 |
В сосуде объемом V = 5 л находится азот массы m = 1,4 г при температуре |
|
|
Т = 1800 К. Найти давление Р газа, имея в виду, что при этой температуре |
|
|
k = 30% молекул диссоциировано на атомы. |
(1,9 атм) |
2.61Во сколько раз изменится температура идеального газа, если уменьшить его объем в два раза при осуществлении процесса, в котором давление и объем
связаны соотношением РV2 = const. |
(в 2 раза) |
2.62В замкнутом сосуде к верхней стенке на пружине жесткостью 4 Н/м
подвешена сфера объемом 2 л. На какую высоту h поднимется сфера, если при постоянной температуре 17 0С давление в сосуде повысить от 100 кПа
до 500 кПа? |
(0,024 м) |
2.63В цилиндрическом сосуде, заполненном газом, объемом V находится подвижная перегородка, расположенная посередине. С одной стороны перегородки давление втрое больше, чем с другой. Перегородку
удерживают неподвижной. Чему равны станут объемы V1 и V2 частей |
|
сосуда, на которые его разделит перегородка, если ее отпустить? |
|
Температура постоянна. |
(0,25V; 0,75 V) |
2.64 |
В цилиндре под поршнем находится газ. Масса поршня 0,6 кг, его площадь |
|
|
20 см2. С какой силой F надо действовать на поршень, чтобы объем газа в |
|
|
цилиндре уменьшился вдвое? Температура газа не изменяется, атмосферное |
|
|
давление нормальное. |
(0,2 кН) |
2.65 |
В цилиндре под поршнем находится воздух. Вес поршня 60 Н, |
площадь |
|
сечения цилиндра 20 см2, атмосферное давление 100 кПа. Груз какой массы |
|
|
m надо положить на поршень, чтобы объем воздуха в цилиндре уменьшился |
|
|
в два раза при постоянной температуре? |
(26 кг) |
2.66В вертикальном закрытом цилиндре находится подвижный поршень, по обе стороны которого находится по одному молю гелия. При равновесии при температуре 320 К объем гелия над поршнем в 4 раза больше объема под поршнем. При какой температуре t отношение объемов станет равным
трем? |
(177 0С) |
2.67Посередине закрытой с обеих концов трубки длиной l = 1 м, расположенной
горизонтально, находится в равновесии подвижная перегородка. Слева от нее температура газа t1 = 100 0C, справа – температура t2 = 0 0C. На каком
38
расстоянии от левого конца трубки установится перегородка ( l1 - ? ), если
температура газа в левой части трубки тоже охладить до 0 0С? |
(0,42 м) |
2.68Один конец цилиндрической трубки, длина которой 25 см и радиус 1 см, закрыт пробкой, а в другой вставлен поршень, который медленно вдвигают
в трубку. Когда поршень подвинется на 8 см, пробка вылетит. Считая температуру постоянной, найти силу трения F пробки о стенки трубки в
момент вылета пробки. Атмосферное давление нормальное. |
(0,015 кН) |
2.2 ФИЗИЧЕСКИЕ ОСНОВЫ ТЕРМОДИНАМИКИ
Основные формулы
1 Средняя кинетическая энергия, приходящаяся на одну степень свободы:
i 
1 kT .
2
Средняя кинетическая энергия (поступательного и вращательного движений) одной молекулы
i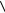 
i kT ,
2
где i – число степеней свoбоды.
Число i степеней свободы есть число независимых координат, определяющих положение молекулы в пространстве. В зависимости от сложности строения i принимает следующие значения:
i = 3 для одноатомных газов; i = 5 для двухатомных газов;
i = 6 для трех- и многоатомных газов (если не учитывать колебаний частей молекул).
Внутренняя энергия и изменение внутренней энергии идеального газа
U i RT m i RT
2 |
2 |
, |
|||||
|
|||||||
U |
i |
R T |
m |
|
i |
R T |
|
|
|
|
, |
||||
2 |
|
2 |
|||||
|
|
||||||
где ν – количество вещества; m – масса газа; ? – молярная масса газа; R – молярная газовая постоянная.
2 Теплоемкость это физическая величина, численно равная теплоте, необходимой для нагревания тела (системы) на один кельвин:
dQ C dT ,
где dQ – теплота, подведенная к телу при повышении его температуры на dT.
39
3 Связь между молярной Cm и удельной с теплоемкостями газа
Cm c ,
где ? – молярная масса газа.
Молярные теплоемкости газа при постоянном объеме и постоянном давлении
C |
i |
R |
, |
C |
i 2 |
R |
. |
|
2 |
2 |
|||||||
V |
|
P |
|
|||||
|
|
|
|
|
|
Отношение γ теплоемкости газа при постоянном давлении к теплоемкости его при постоянном объеме выражается формулой
CP i 2 .
CV i
Уравнение Майера. Разность теплоемкостей газов при постоянном давлении и постоянном объеме равна универсальной газовой постоянной
CP CV R .
4 Первое начало термодинамики в общем случае
Q U A ,
где Q – количество теплоты, сообщенное газу или отданное им; ΔU – изменение ее внутренней энергии; A – работа, совершаемая газом против внешних сил. Первое начало термодинамики для малого изменения системы
dQ dU dA .
Работа, совершаемая газом при изменении его объема:
dA pdV .
Полная работа при изменении объема газа
V 2
A pdV ,
V 1
где V1 и V2 - соответственно начальный и конечный объемы газа. а) Изохорический процесс (V = const)
V 0, A 0,
Q U .
б) Изобарический процесс ( p = const)
A p V R T,
Q U A .
в) Изотермический процесс (T = const)
40
T 0, U 0, A RT lnV2 , V1
Q A .
г) Адиабатический процесс (Q = 0)
A U .
5 Уравнение адиабатического процесса (уравнение Пуассона)
PV const .
Начальное и конечное значения давления, объема и температуры связаны соотношениями:
P |
V |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||
2 |
|
1 |
|
T2 |
|
V1 |
|
, |
T2 |
P |
|
||||||||
|
T |
|
|||||||
V |
, |
V |
|
T |
|||||
1 |
2 |
|
1 |
2 |
|
|
1 |
||
|
P2 |
|
1 |
|
|
||||
|
|
|
|
|
P |
|
|
||
|
. |
|||
|
1 |
|
|
|
6 Термический коэффициент полезного действия для кругового процесса – цикла (характеризует степень использования теплоты при превращении ее в работу):
|
A |
|
Q1 Q2 |
1 |
Q2 |
|
|
Q |
Q |
Q , |
|||||
|
|
|
|||||
1 |
1 |
1 |
|
||||
где Q1 – количество теплоты, полученное системой; Q2 – количество теплоты, отданное системой; А – работа, совершаемая за цикл.
Термический коэффициент полезного действия цикла Карно
|
Q1 Q2 |
|
T1 T2 |
|
|
|
|||
|
Q1 |
, |
||
|
|
T1 |
||
где Т1 – температура нагревателя; Т2 – температура холодильника.
7 Изменение энтропии при равновесном переходе из состояния 1 в состояние 2
|
|
|
|
2 |
|
dQ |
|
|
|
|
2 |
dU dA |
|
|||||||||||
S1 2 S2 S1 |
|
|
. |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||
Для изохорического процесса |
|
|
|
1 |
|
T |
|
1 |
|
|
|
T |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T2 |
|
|
|
|
||||
2 |
dU |
|
|
|
|
|
i m |
|
dT |
|||||||||||||||
S1 2 1 |
|
|
|
|
|
|
|
|
|
|
|
|
RT |
|
|
. |
||||||||
T |
|
|
2 |
|
T |
|||||||||||||||||||
Для изотермического процесса |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
2 dA |
|
|
|
|
|
|
m |
|
T2 |
|
dT |
||||||||||||
S1 2 1 |
|
|
|
|
|
|
|
R T |
|
|
|
. |
||||||||||||
T |
|
|
|
|
|
|
T |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||
Для изобарического процесса