
физ / обербек 3.1-3
.5.pdfМИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
УФИМСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЯНОЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
КАФЕДРА ФИЗИКИ
ДИНАМИКА
ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
Методические указания к лабораторным работам
№ 3-1..3-5
по разделу «Физические основы механики»
У Ф А 2 0 0 3
1
Методические указания содержат описания пяти лабораторных работ по теме "Динамика вращательного движения твердого тела" и краткие сведения по теории. Предназначена для студентов всех специальностей и всех форм обучения УГНТУ при выполнении лабораторного практикума по курсу общей физики, раздел "Физические основы механики".
Составители: Маненкова Л. К., канд. физ. − мат. наук, доцент Лейберт Б.М., канд. техн. наук, доцент
Рецензент Пестряев Е. М., канд. физ. − мат. наук, доцент
© Уфимский государственный нефтяной технический университет,
2003
1
ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
Простейшая форма движения − это механическое движение, которое характеризуется изменением взаимного расположения тел или их частей относительно друг друга в пространстве с течением времени.
Абсолютно твердое тело можно рассматривать как систему материальных точек, расстояние между которыми неизменно.
Любое сложное движение твердого тела можно рассматривать как сумму двух простых: поступательного и вращательного.
При поступательном движении каждая линия, соединяющая две любые точки тела, сохраняет свое неизменное направление в пространстве.
Вращательным движением твердого тела называется такое, при котором траектории всех точек тела являются концентрическими окружностями с центром на одной прямой, называемой осью вращения.
Вращательное движение характеризуется угловой скоростью вращения ω и угловым ускорением ε, которые определяются по формулам:
ω = |
dϕ |
; |
|
ε = |
dω |
|
= |
d 2ϕ |
|
|||
|
|
dt |
|
dt 2 |
||||||||
|
|
dt |
|
|
|
|||||||
где |
ϕ − угловое перемещение тела или угол поворота. Длина дуги ок- |
|||||||||||
ружности S с радиусом r, равна |
S = ϕ r. Связь между линейной V и угло- |
|||||||||||
вой скоростью ω, |
линейным aτ и угловым ε ускорением следующая: |
|||||||||||
|
|
|
|
|
|
|
V =ω r; |
|
aτ =ε r |
|||
M |
|
|
|
F |
Вращающим моментом силы называется векторная |
|||||||
|
|
|
|
физическая величина, равная произведению радиуса- |
||||||||
r |
|
|
|
α |
вектора |
r проведенного из точки O в точку приложения |
||||||
|
|
|
силы F (т. А) на вектор силы: |
|||||||||
φ |
|
|
|
|||||||||
|
|
А |
|
|
M =[r,F] |
|||||||
|
|
|
|
|
||||||||
Рис.1 |
Вектор M направлен по оси вращения и определяет |
|||
направление углового ускорения |
ε. Векторы |
r, F, M |
||
|
||||
образуют правый винт.
Моментом силы относительно точки или неподвижной оси называется скалярная величина, численно равная произведению силы F на плечо l, т.е. кратчайшее расстояние от оси вращения до линии действия силы (рис. 1):
M = F l = F r sinα
Инертные свойства тела при вращении характеризуются не его массой m, как при поступательном движении, а физической величиной, называемой моментом инерции тела относительно данной оси вращения I.

2
Моментом инерции материальной точки, находящейся на расстоянии r от какой-либо оси является величина
I = m r2 .
Момент инерции твердого тела относительно оси вращения:
I = ∑i mi ri2 =∫ ρ r2dV ,
V
где ρ − плотность тела, dV − элемент его объема.
Обычно вычисляют момент инерции тела относительно оси проходящей через центр масс тела I0. Тогда момент инерции тела относительно произвольной оси, параллельной оси, проходящей через центр масс тела, равен
I = I0 + m d 2 ,
где m − масса тела, d − расстояние между осями вращения. Эта формула выражает теорему Штейнера.
Основной закон динамики вращательного движения твердого тела, для
которого I = const имеет вид:
M = I е,
где M − вращающий момент, I − момент инерции тела, ε − его угловое ускорение. Этот закон можно записать в другом виде:
M dt = d(I щ)
Импульс момента силы равен изменению момента импульса тела.
|
Вектор L = I ω называется моментом импульса тела. |
Если имеем точ- |
|
ку, вращающуюся по окружности с линейной скоростью V, |
то ее момент им- |
||
пульса будет: |
|
||
|
|
|
|
Вращающееся тело обладает кинетической энергией
3
ЛАБОРАТОРНАЯ РАБОТА № 3 - 1
Изучение основного закона вращательного движения твердого тела на маятнике Обербека
Цель работы: экспериментальная проверка основного закона динамики вращательного движения.
Приборы и принадлежности: маятник Обербека, секундомер, штангенциркуль, линейка, набор грузов.
l
R2
m0
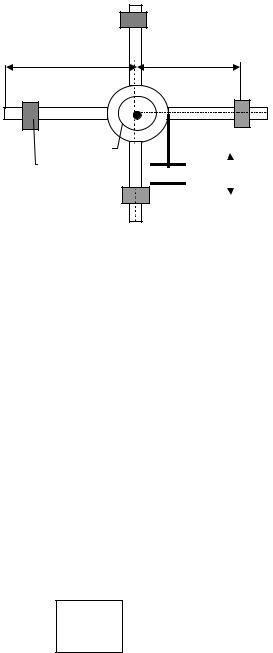
Описание установки
R
 R1
R1
T


 a mg
a mg
Маятник Обербека представляет собой крестовину (рис. 1), вращающуюся вокруг горизонтальной оси. С крестовиной скреп-  лены два шкива радиусами R1 и R2, на которые можно наматывать нить с грузом массы m. Сила натяжения нити T (при опускании груза) приводит во вращение крестовину. На стержнях крестовины на одинаковых расстояниях R от оси вращения ук-
лены два шкива радиусами R1 и R2, на которые можно наматывать нить с грузом массы m. Сила натяжения нити T (при опускании груза) приводит во вращение крестовину. На стержнях крестовины на одинаковых расстояниях R от оси вращения ук-
репляют четыре одинаковых груза m0, размеры которых малы по сравнению с R. Высоту опускания h груза m отсчитывают по
вертикальной линейке. В отсутствии грузов на стержнях прибор имеет некоторый собственный момент инерции I0, величина которого определяется, главным образом, моментом инерции стержней. При грузах на стержнях момент
инерции крестовины будет I = I0 + 4 m0 R2, |
если грузы принять за матери- |
|
альные точки. |
|
|
Уравнения движения крестовины и груза |
|
|
M − M тр = I е |
(1) |
|
m g −T = m a |
||
|
||
Момент силы в данном случае: |
|
|
M =T R1 = m (g −a) R1 |
(2) |
Ускорение груза m определяется из формулы пути равноускоренного движения
(3)
а угловое ускорение маятника ε будет
|
|
|
|
4 |
ε = |
a |
|
|
(4) |
R1 |
|
|||
|
|
|||
|
|
|
||
Mтр− момент сил трения, действующий на крестовину. Высота, с кото- |
||||
рой опускается груз |
h, и |
время его опускания t измеряют в ходе эксперимен- |
||
та. Вычисляя затем |
M и |
ε из графика зависимости M = M(ε), находят Mтр |
||
и момент инерции маятника, значение которого сравнивается с расчетным.
Упражнение 1. Определение момента инерции маятника при разных шкивах (R1, R2).
Порядок выполнения работы и обработка результатов 1. Подготавливают протокол и таблицу для записи результатов измере-
ний.
2.Измеряют штангенциркулем диаметр большого (2 R1) и малого (2 R2) шкива. Точность измерения, то есть ошибка измерения при этом 0,1 мм.
3.На технических весах измеряется масса груза m. Точность измерения
m = 0,5 г. Величина m может быть так же задана. В последнем случае ошибка m равна половине последнего разряда числа, представляющего массу.
4. На шкив наматывается нить, на конце которой укреплен груз m, так чтобы он был на высоте h над уровнем пола. Масштабной линейкой измеряется h с точностью h.
5.Предоставив грузу m возможность падать, по секундомеру замеряют время падения. Секундомер включают в момент начала падения груза и выключают одновременно с ударом груза о пол.
6.По формулам (3), (4), (2) вычисляют линейное, угловое ускорение, вращающий момент силы. Опыты проводятся не менее трех раз для каждого шкива при неизменном симметричном расположении цилиндрических грузов
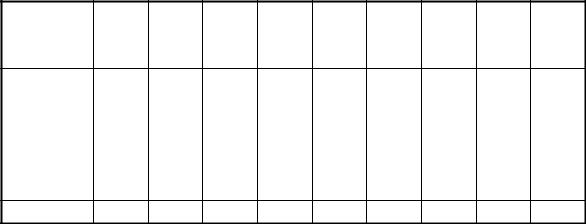
m0 на стержнях, на одном и том же расстоянии от оси. Результаты измерений и вычислений заносят в таблицу 1. Таблица 1
N |
|
оп R h t |
t a ε M Mтр I |
ыта |
|
1
R1
2
3
Сре
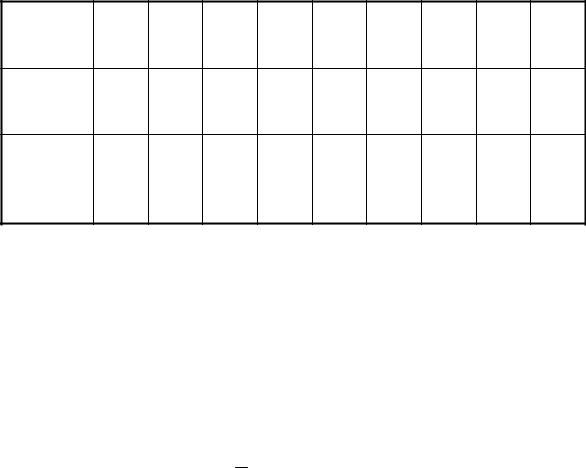
5
днее
зна
чение
1
2
3 R2
Сре
днее
зна
чение
7. Вычисляют относительные и абсолютные погрешности для a, ε, M.
8. Строят график |
M |
от |
ε и, продолжая прямую до пересечения с осью |
|||
М, находят Mтр. |
|
|
M − MΤΡ |
|
||
9. Из формулы |
I |
= |
находят моменты инерции для экс- |
|||
|
ε |
|||||
|
|
|
|
|
||
периментов с обоими шкивами I1 и I2.
10.Вычисляют относительную и абсолютную погрешность для I.
11.Рассчитывают момент инерции по формуле
I = I0 + 4m0 R2 = 4 13 mcl2 + 4m0 R2
где R - расстояния каждого из четырех цилиндров от оси вращения, l - длины каждого из четырех стержней, m0 и mс - массы цилиндрических грузов и стержня (заданы).
12. Вычислив теоретическое значение момента инерции маятника, проверяют соответствие теоретических и экспериментальных значений моментов инерции. Для этого определяется интервал возможных значений для момента
инерции [ I − I, I + I ], где |
I = |
I1 + I 2 |
|
2 |
|||
|
|
Соответствие удовлетворительное, если I* принадлежит этому интервалу.
Упражнение 2. Определение момента инерции маятника для разных грузов m.
В этом упражнении вращающий момент изменяют путем изменения величины груза m. Опыты проводят с одним из шкивов, например, R1.
Порядок выполнения и обработка результатов опытов такая же как и в упражнении 1.
Результаты опытов заносят в таблицу 2. Таблица 2
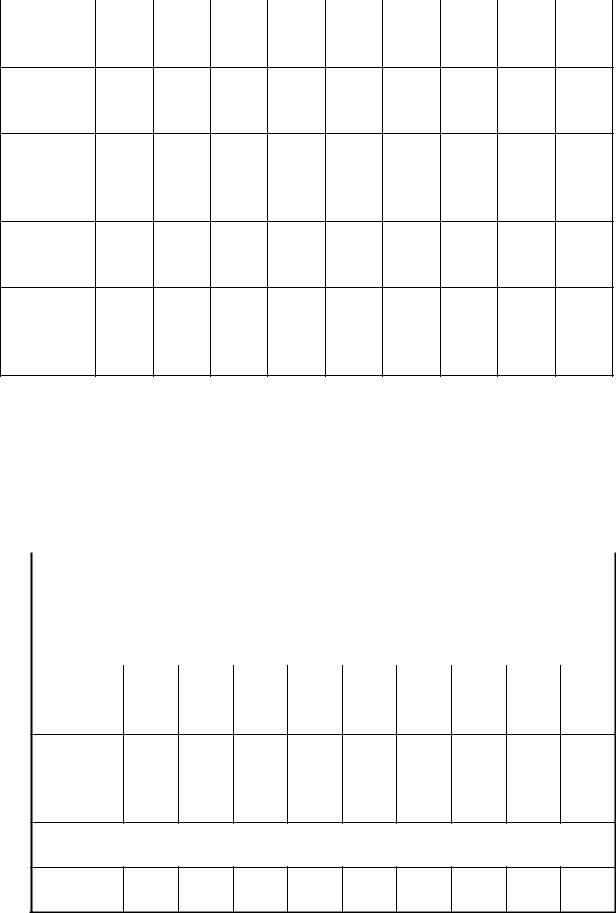
|
6 |
|
|
N |
t a ε M Mтр I |
опы m h t |
|
та |
|
1
2
3 m1
Сре
днее
зна-
чение
1
2
3 m2
Сре
днее
зна-
чение
Упражнение 3. Определение момента инерции маятника при разных положениях цилиндрических грузов m
В этом упражнении вращающий момент остается неизменным. Все опыты проводятся с одним из шкивов, например, R1 и с одним из грузов m. Меняется лишь расстояние R.
Порядок выполнения и обработка результатов опытов как и в упражнении 1. Результаты опытов заносят в таблицу 3.
Таблица 3
N |
R |
h |
t |
t |
a |
ε |
M |
Mтр |
I |
опыта |
|
|
|
|
|
|
|
|
|
|
|
Цилиндрические грузы расположены у шкива |
|||||||
1 |
|
|
|
|
|
|
|
|
|
2 |
R’ |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
Сре
днее
зна
чение
Цилиндрические грузы расположены на концах стерж-
ней
1
2

7
3 R"
Сре
днее
зна
чение
Теоретические значения моментов инерции маятника рассчитывают для
двух случаев:
I′т = I0 + 4mR′2 и I″т = I0 + 4mR″2,
и каждое из них сравнивают с соответствующим опытным значением.
Упражнение 4. Определение степени диссипации механической энергии маятника
Если маятник Обербека рассматривать как консервативную систему, то можно применить закон сохранения механической энергии.
За счет потенциальной энергии груза m, поднятого на высоту h, вращаю-
щаяся часть системы получает кинетическую энергию |
Iω |
2 |
, а сам груз - кине- |
|||
2 |
|
|||||
|
mV 2 |
|
|
|
||
тическую энергию |
. Таким образом закон сохранения механической энер- |
|||||
2 |
||||||
|
|
|
|
|
||
гии для данного случая запишется так:
mgh = |
Iω |
2 |
+ |
mV 2 |
(5) |
2 |
|
2 |
|||
|
|
|
|
Скорость груза m в конце пути h найдется из равенства
V = a t, |
(6) |
а угловая скорость из равенства |
|
ω = |
V |
, |
(7) |
|
|
R |
|||
где R - радиус шкива |
|
|||
Однако из-за наличия трения правая часть равенства (5) всегда оказывается больше левой, так как наша система оказывается диссипативной, т.е. такой, в которой механическая энергия не остается постоянной, а непрерывно уменьшается, переходя в другие (не механические) формы энергии, например в энергию теплового движения молекул. Разность между левой и правой частями равенства является мерой диссипации (рассеяния) энергии и равна работе по преодолению сил трения. Долю диссипированной механической энергии найдем из равенства
