физика лекц / Лекция 4

Лекция 4.

ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ.

4.1. Вращение твердого тела вокруг неподвижной оси. Момент инерции. Момент силы.

При вращательном движении все точки твердого тела в каж­дый момент времени имеют одинаковые угловые скорости ω и ускорения ε. Линейные же скорости и ускорения для этих же то­чек пропорциональны расстоянию r частиц до оси вращения, и определяются известными формулами:

υ = ω ∙ r и a = ε ∙ r

Определим кинетическую энергию вращающегося тела вокруг про­ходящей через него неподвижной оси. Мысленно разобьем тело на малые отдельные объемы с массой m_i на расстоянии r_i от оси враще­ния (рис.1.4). Если тело вращается с угловой скоростью ω_i, то кинетическая энергия i - того объема

равна m_iυ_i , а всего тела:

W = (m₁υ₁² + m₂υ₂² + ... +m_nυ_n²) = ω² (m₁r₁² + m₂r₂² + ... + m_nr_n²)

Величина называется моментом инерции материальной точки относительно оси вращения.

Сумма называется моментом инерции тела относительно оси вращения, или

m_i

r_i

Рис.4.1

(4.1)

Момент инерции тела (точки) характеризует инерционные свойства тела (точки) относительно выбранной оси вращения.

Кинетическая энергия вращающегося тела определяется уравнением:

(4.2)

Произвольное движение твердого тела можно рассматривать как совокупность поступательного движения тела со скоростью центра инерции  и вращательного движения вокруг оси, проходящей через центр инерции.

(4.3)

Пользуясь формулой (4.1), можно вычислить, например, момент инерции однородного стержня длинной l, и массой m относительно оси, проходящей через конец стержня (рис.4.2). l

Из рисунка dm = ∙ dr . Применив (4.1), получим  = = (4.4)

Pис.4.2

Если известен момент инерции относительно оси, проходящей через центр инерции тела ₀ , то можно вычислить момент инерции  относительно параллельной оси на произвольном расстоянии d от первой оси по теореме Штейнера (рис.4.3):

=₀ + md² , (4.5) где m – масса тела.

где m - масса тела.

Эта формула является математическим выражеием теории Штейнера. Момент инерции Ј относительно произвольной оси равен сумме момента инерции ₀ относительно оси параллелной данной и проходящей через центр инерции тела, и произведения массы тела m на квадрат расстояния между осями.

Рис. 4.3. Пусть вокруг оси вращается тело (рис.4.4). На рисунке ось 0 перпендикулярна плоскости чертежа. Ясно, что силы, направленные параллельно оси вращения, могут лишь сдвинуть тело вдоль оси, но не могут произвести вращения. Поэтому можно рассмат­ривать только силы, лежащие в плоскости, перпендикулярной оси вращения. Момент такой силы относительно оси 0 дается величиной векторного

произведения r ∙ F, где r - вектор расстояния точки приложения силы от оси. Точка A есть точка приложения силы. По определению векторного произведения имеем:

(4.6)

где  - угол между F и r . Иначе можно записать M=lF, где l = r ∙ sinθ - плечо силы (расстояние от оси до направления действия силы). M - псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от r к F.

4.2. Основное уравнение динамики вращательного движения.

Рассмотрим цилиндр, вращающийся вокруг

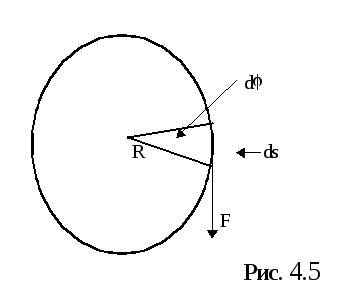
неподвижной оси (рис.4.5) под действием

постоянной силы F. За время dt точка приложения силы переместится на dS и работа этой силы будет

dA = F dS, которая при отсутствии сопротивления

равна изменению кинетической энергии.

т.к. , то

Произведение Fr есть величина, называемая моментом M силы F относительно оси вращения 0. Поэтому запишем

или

, но , откуда

M =  ∙ ε (4.7)

В векторной форме M =  ∙ ε (4.8)

Полученная формула носит название основного уравнения динамики вращательного движения. Момент силы, приложенный к телу, численно равен произведению момента инерции на угловое ускорение. Она выражает второй закон Ньютона для вращательного движения. Роль силы при вращательном движении играет момент силы, роль массы - момент инерции тела. Момент силы M является векторной величиной, направленной вдоль оси вращения. Из уравнения (4.8) видно, что направление вектора совпадает с направлением вектора углового ускорения .

Из вывода (4.8) можно найти выражение для работы при вращении тела:

dA = F dS = F r d = M d, (4.9)

т.е. работа при вращении тела равна произведению момента действующей силы на угол поворота.

4.3. Момент импульса. Закон сохранения момента импульса.

Пусть твердое тело вращается вокруг неподвижной оси с постоянной угловой скоростью . Мысленно разделим его на элементарные частицы. Тогда m_i - масса частицы, υ_i - линейная скорость по окружности, r_i - радиус окружности. Величина m_i _i r_i - называется моментом импульса частицы (L_i). Учитывая, что _i =  r_i , получим

L_i = J_i  (4.10)

Для твердого тела в целом:

.

Векторная величина

L = Jω (4.11)

называется моментом импульса системы относительно оси вращения. Направления векторов L и ω совпадают.

Подставив в (4.8) ε = , получим

M = (4.12)

Это наиболее общий вид уравнения (4.8). Если суммарный момент внешних сил, действующих на тело, равен нулю, то из формулы (4.12).

следует, что = 0 или

L = Jω = const (4.13)

Уравнение (4.13) выражает закон сохранения момент импульса: если на вращающееся тело (систему частиц) не действуют внешние силы или их результирующий момент равен нулю, момент импульса тела (системы частиц) по отношению к заданной оси (точке) есть величина постоянная.

Для замкнутой системы этот закон можно записать в виде следующего уравенния

(4.13’)

Ясно, что если изменится момент инерции тела, то должна измениться и угловая скорость. Это можно продемонстрировать на скамье Жуковского. Зависимость используется фигуристом при вращении на льду, спортсменами в акробатике и т.д. Закон сохранения момента импульса относится к фундаментальным законам природы, имеет более общий характер, чем закон сохранения импульса. Он применим и к телам с незакрепленной осью, когда наблюдается гироскопический эффект, широко применяемый в практических устройствах: гирокомпас, автопилот, велосипед и т.д. Следует отметить, что подробная теория гироскопов достаточно объемна и сложна.