физика лекц / Лекция 3

15

3. ИНЕРЦИАЛЬНЫЕ И НЕИНЕРЦИАЛЬНЫЕ ИСТЕМЫ ,

РАБОТА И ЭНЕРГИЯ . ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ.

3.1. Принцип относительности Галилея.

Любая система отчета, которая движется прямолинейно и равномерно относительно некоторой инерциальной системы отчета, также является инерциальной, т.е. инерциальных систем имеется бесчисленное множество.

Рассмотрим две системы отчета, движущиеся относительно друг друга с постояной скоростью υ_о .

Пусть X, Y, Z координаты в неподвижной , а в движущейся системе. Движется система прямолинейно и равномерно со скоростью v₀ (рис.3.1.) вдоль оси X.. Через время t координаты точки А будут:

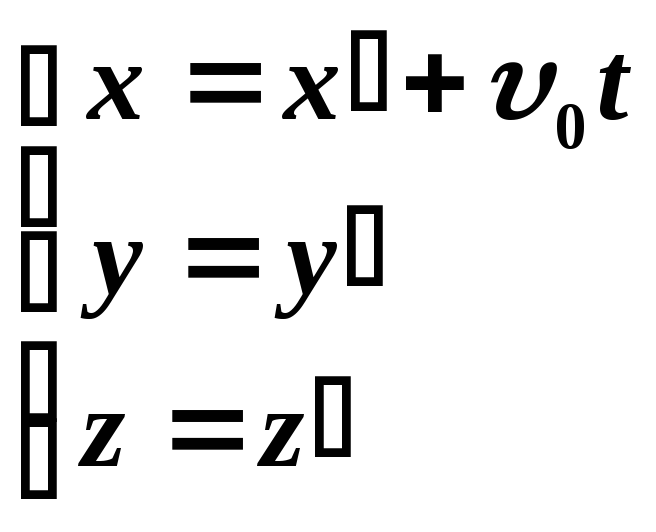(3.1)

Рис.3.1.

Соотношения (3.1.) называются преобразованиями Галилея. С их помощью осуществляется переход от движущейся системы к неподвижной и наоборот.

Продифференцировав (3.1.) по времени, получим

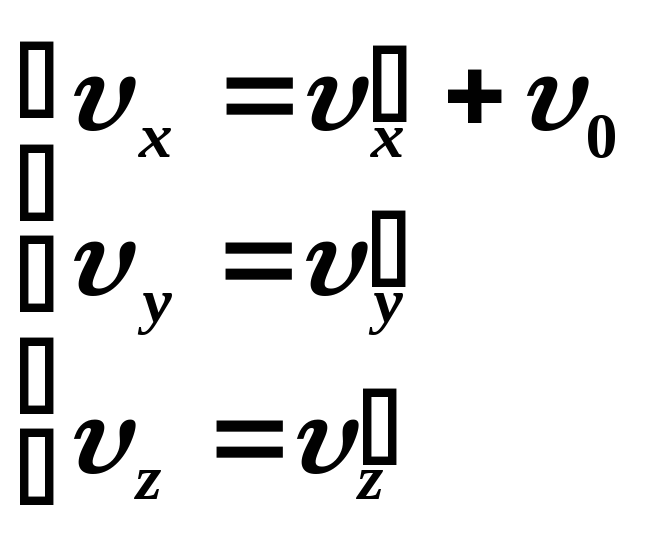
В векторной форме эти уравнения представляются одним равенством:

υ = υ` + υ_о (3.2)

Это принцип сложения скоростей . В результате дифференцирования по t (3.2.) получим:

a = a` (3.3)

Равенство ускорений показывает, что взаимодействие тел в обеих системах происходит одинаково. Если в системах выполняются законы Ньютона, то такие системы называют инерциальными. Согласно (3.3) система движущаяся прямолинейно и равномерно относительно инерциальной, также инерциальная. Из равенства (3.3) следует и принцип относительности Галилея: ”Никакими механическими опытами, находясь внутри инерциальной системы нельзя установить, находится она в покое или равномерном прямолинейном движении”.

А.Эйнштейн обобщил этот принцип, что и послужило одним из двух постулатов теории относительности.

Системы отсчета, движущиеся с ускорением относительно инерциальных систем, являются неинерциальными. Законы Ньютона выполняются в них только с поправками на, так называемые инерционные силы.

Инерционные силы проявляются в следующих случаях:

а) силы инерции при ускоренном поступательном движении системы отсчета ;

б) силы инерции, действующие на тело, покоящееся во вращающейся системе;

в) силы инерции, действующие на движущиеся тела во вращающейся системе.

В первом случае - это обычные силы инерции, возникающие, например, в транспорте при торможении и ускорении: F_m = -ma . Они направлены всегда противоположно ускорению системы и не являются результатом взаимодействия тел. Во вращающейся системе на тела действуют инерционные силы, называемые центробежными. Известно: F_Uо = . Если тело движется во вращающейся системе, то кроме центробежных сил на него действует сила Кориолиса, вычисляемая по формуле:

F_к = 2mυ`ω

где ω - угловая скорость вращения системы, а υ` - скорость движения тела в системе.

Силы инерции вызываются не взаимодействием тел, а ускоренным движением системы отсчета. поэтому они не подчиняются третьему закону Ньютона. Для любого из тел в инерциальной системе силы инерции являются внешними, т.е. здесь нет замкнутых систем.

3.2. Работа. Кинетическая и потенциальная энергии.

Универсальной мерой различных форм движения и взаимодействия служит физическая величина, называемая энергией. Энергия характеризует систему с точки зрения качественных превращений и количественных изменений движения. Изменение энергии тела является результатом силового взаимодействия тела с другими телами. Для количественной характеристики этого процесса вводится понятие работы силы.

Работой силы F на перемещении dS называется величина, численно равная произведению прекции этой силы F_S на направление перемещения на величину самого перемещения.

Если сила F постоянна, а тело, к которому она приложена, движется поступательно и прямолинейно, то работа, совершаемая силой F, при прохождении пути S, определяется формулой:

A=FScos = F_sS, (3.4)

где  -угол между направлением силы F и перемещения S .

F_s = Fcos ­­­­­­­­­­­­­­­­- проекция силы F на направление перемещения. В общем случае движения тела по криволинейной траектории под действием переменной силы сначала находят элементарную работу dA на малом перемещении dS, на котором модуль и направление силы можно считать неизменными, а траекторию прямолинейной:

dA = F_s dS (3.5)

Суммарную работу А силы на участке траектории от точки 1 до точки 2 находят интегрированием:

Работа - скалярная величина, измеряется в джоулях(Дж). Работу за единицу времени называют мощностью.

N = или N = F • υ (3.6)

Мощность тоже скаляр. Измеряется в ваттах ( 736 Вт = 1 л.с. )

В механике различают два вида энергии: кинетическую и потенциальную. Кинетической энергией тела называют энергию, измеряемую работой, которую может совершить движущееся тело при изменении скорости от до . Элементарная работа силы F_S на пути dS равна :

dA = F_s ∙ dS = m ∙ dS = mυ ∙dυ , отсюда

A = = – = W_k2 – W_k1 (3.7)

Cогласно (3.7.) работа результирующей силы равна приращению кинетической энергии тела. Для элементарной работы можно записать: dA=dW_k

Потенциальная энергия механической системы, это энергия, которая зависит только от взаимного расположения взаимодействующих частей системы и от их положения во внешнем силовом поле. Под силовым полем понимается пространство, в каждой точке которого на тело действует определенная сила. В частном случае это силы, действующие на тело, поднятое над Землей. Если силовое поле не зависит от времени, а при движении в нем тела по замкнутому пути, работа сил поля равна нулю, т.е. работа в таком поле зависит лишь от начального и конечного положений точек перемещения, то такие поля называют потенциальными, а действующие в них силы консервативными.

Консервативные силы характеризуются отсутствием перехода энергии в другие немеханические виды. Если же работа зависит от траектории, то силы диссипативные (например, сила трения). При этом механическая энергия переходит частично в теплоту.

Тело, находясь в потенциальном поле сил, обладает потенциальной энергией. Работа консервативных сил при элементарном изменении конфигурации системы равна приращению потенциальной энергии, взятому со знаком минус, т.к. работа совершается за счет убыли потенциальной энергии:

dA = - dW_п (3.8)

Найдем связь потенциальной энергии и силы. Известно ,

F_sdS= -dW_п или F_s = , отсюда

F = -gradW_п (3.9)

т.е. сила равна градиенту потенциальной энергии со знаком минус. Соотношение (3.9) записано в векторном виде, при этом:

gradW_п = i + j + k

где - единичные векторы координатных осей, а сам вектор называется градиентом скаляра . Для выражения применяется обозначение . Это символический вектор, его называют оператором Гамильтона или набла-оператором:

= i + j + k (3.10)

Поэтому (3.9) может иметь вид: F = - W_п (3.11)

Известно, что с помощью формулы работы можно вычислить

потенциальную энергию массы m в поле Земли на высотах и :

W_п = mgh₂ – mgh₁ (3.12)

Потенциальная энергия определяется и другой формулой (3.12). Например, потенциальная энергия сжатой пружины

W_п = (3.13)

Действительно, из формул F= -kx., dA=Fdx, найдем

dA=dW_п = -kxdx. Интегрируя последнее, получим (3.13).

3.3. Закон сохранения энергии в механике.

Полной механической энергией системы называют величину W, равную сумме кинетической и потенциальной энергий этой системы:

W = W_п + W_к

Полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остается постоянной (закон сохранения энергии в механике).

Для доказательства закона сохранения механической энергии рассмотрим систему материальных точек движущихся со скоростями Запишем по второму закону Ньютона уравнения для каждой точки, как и в случае доказательства закона сохранения импульса:

m₁= (F_1-2 + F_1-3 + F_1-n) + F₁^*

... ... ... ... ... ... ... ...

m_n= (F_n-1 + F_n-2 + F_n(n-1)) + F_n^*

F_1, F₂ ......F_n - это внешние неконсервативные силы, кроме того в скобках, в отличие от доказательства закона сохранения импульса, могут быть не только консервативные внутренние силы, но и внешние консервативные, т.е. сумма в скобках не равна нулю.

Каждое из уравнений умножим на υ₁dt = dr и, сложив все равенства почленно, получим:

Если внешние консервативные силы отсутствуют, то с учетом, что

, а второй член равен убыли потенциальной энергии -, можно записать

dW_к + dW_п = 0 или d(W_к + W_п) = 0, откуда

W_к + W_п = const

Таким образом, доказали, что полная механическая энергия системы сохраняется постоянной. Из доказательства следует, что это закон для систем, где действуют только консервативные силы.