физика лекц / Лекция 21

Лекция 21.

ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ.

21.1. Гипотеза де-Бройля.

Как известно, действенность во взглядах на природу света получила название корпускулярно-волнового дуализма.

В 1924 г. Луи де Бройль высказал предположение, что это двойственная природа характерна не только для света, а имеет универсальный характер. Частицы вещества должны обладать не только корпускулярными, но и волн волновыми свойствами. Из этого следовало, что формулы характеризующие фотоны света, должны распространяться на частицы. Для фотонов справедливы соотношения:

Из последней формулы получим (21.1)

или (21.1`)

По гипотезе де Бройля (21.1) можно применить для определения длины волны элементарной частицы (электрона, протона и т.д.). Зависимость (21.1) называют еще формулой де Бройля.

В релятивистском случае, когда масса частицы зависит от ее массы и скорости, т.е. 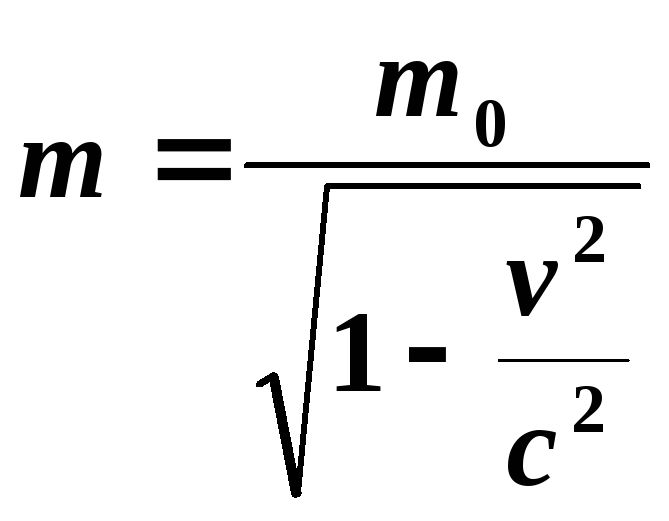, то ,

где m_о - масса покоящейся частицы, m - масса частицы, движущейся со скоростью , h - постоянная Планка. Для электрона в электронно-лучевой трубке с ускоряющем напряжением 2кВ   0,3 А. Известно, что видимый свет имеет 5500 А, поэтому обнаружить волну такой длины достаточно трудно.

Рис. 21.1

Гипотеза де Бройля в 1927 г. была подтверждена экспериментально, в опытах Дэвиссона и Джермена. Схема опытов изображена на рис. 21.1. Электроны из электронной пушки отражались и рассеивались на

монокристалле никеля или лития, затем улавливались по разным направлениям электронной ловушкой

и их интенсивность измерялась включенным гальванометром.

Зависимость интенсивности отраженных электронов от угла рассеяния имела вид, изображенный на рис. 21.2, т.е. наблюдалась типичная дифракционная картина. Дифракционная картина, рассчитанная по формуле (21.1) и экспериментальная хорошо совпадают. Таким образом опытным путем подтверждена гипотеза де Бройля.

Позднее она подтверждалась неоднократно, например, в опытах Тартаковского и Томсона при рассеянии электронов на фольге, в опытах В.А.Фабриканта с отдельным электроном.

Рис. 21.2

20.2. Соотношение неопределенностей Гейзенберга

Если частица - волна, то как же определить ее точное положение в пространстве? В 1927 г. это рассмотрел Гейзенберг. Материальная точка определяется в пространстве в каждый момент времени координатами и скоростью, т.е. импульсом. На основании можно определить в любой последующий момент времени и координату и импульс, причем с какой угодно точностью.

Это в классической механике, а для элементарной частицы, как показал Гейзенберг, координата и импульс определяются, лишь, с какой-то точностью x и y .

Чтобы определить положение и импульс, например, электрона, его надо "осветить" фотонами и получить рассеянный фотон. В следствие дифракции, определение координаты не может быть точнее  , т.е. x  . При рассеянии фотона у электрона изменяется импульс на величину

p_x порядка импульса фотона: p=h/ .

Отсюда погрешность в определениях: x p > h/ > h

Аналогично для других координат, т.е.

x p_x > h

y p_y > h (21.2)

z p_z > h

Зависимости (21.2) называются соотношениями неопределенностей Гейзенберга. Они существуют не только для координат и импульсов. Например, частица с энергией W на определенном энергетическом уровне находится в течение времени t. В этом случае соотношение неопределенностей

W t > h

Соотношение неопределенностей имеют принципиальный характер. Их нельзя связывать с уровнем развития физики. Они служат критерием насколько можно применять понятия классической механики к микромиру.

21.3. Волновая функция и ее статистический смысл

Волны де Бройля не электромагнитные, они имеют квантовую природу и не имеют аналогов в классической физике. Известно, что любая волна по природе характеризуется волновой функцией. В квантовой механике состояние списывается с помощью волновой функции . Физический смысл волновой функции (или  - функции) можно показать на примере дифракции электронов.

С волновой точки зрения наличие максимумов числа электронов в некоторых направлениях означает, что эти направления соответствуют наибольшей интенсивности волн де Бройля. Но интенсивность пропорциональна квадрату амплитуды волны ( I ~ [A]² ). В нашем случае A . Интенсивность дает вероятность того, что частица находится в этой точке, т.е. []² - квадрат модуля амплитуды волн де-Бройля в данной точке определяет вероятность того, что частица находится в этой точке.

Вероятность dW того, что частица находится в элементе объема dV , пропорциональна []² и dV , т.е. dW=[]²dV

Физический смысл имеет не сама функция  , а квадрат ее модуля: ||² = ^*

(где ^* - функция, комплексно сопряженная с  ). Величина []² имеет смысл плотности вероятности

(21.3)

т.е. определяет вероятность пребывания частицы в данной точке пространства. Вот почему волны де-Бройля называют иногда "волнами вероятности". Волновая функция должна удовлетворять условию нормировки

(21.4)

Действительно, вероятность найти частицу во всем бесконечном пространстве: равна единице. Условие (21.4) говорит об объективном существовании частицы во времени и пространстве.

Из физического смысла волновой функции следует, что она должна быть однозначной, конечной, непрерывной во всех областях изменения координат. Волновая функция - основная характеристика состояния объектов в микромире, находится она путем решения уравнения Шредингера

21.4. Уравнение Шредингера

Уравнение Шредингера играет в квантовой механике такую же роль, что и уравнение Ньютона в классической механике. Как и уравнение движения Ньютона в классической механике, уравнение Шредингера в квантовой механике не выводится, а постулируется. Уравнение нельзя вывести из каких-либо известных ранее соотношений. Справедливость его доказывается тем, что выводы квантовой механики, полученные с помощью этого уравнения в атомной и ядерной физике, находятся в хорошем согласии с опытом.

Уравнение Шредингера имеет вид:

(21.4)

Оно было предложено Шредингером в 1926 г. и называется временным уравнением Шредингера (уравнение Шредингера со временем). Здесь: - приведенная постоянная Планка; m - масса частицы; i - мнимая единица;  - оператор Лапласа, а

- в декартовых координатах.

Как следует из уравнения, вид волновой функции  определяется потенциальной энергией U , т.е. характером сил действующих на частицу. Вообще говоря потенциальная энергия U есть функция координат и времени: U=U(x,y,z,t).

Для стационарного силового поля (т.е. не изменяющегося во времени) U не зависит явно от времени, U = U(t) и является функций только координат: U=U(x,y,z). Оказывается, в этом случае волновая функция распадается на два множителя, один из которых зависит только от времени, второй - только от координат:

(x,y,z,t)=(x,y,z), где E - полная энергия частицы.

Подставляя это выражение во временное уравнение Шредингера, получаем:

Сокращая на общий множитель , запишем

или (21.5)

Уравнение (21.5) называется уравнением Шредингера для стационарной состояний или стационарное уравнение Шредингера. В стационарное уравнение Шредингера входит в качестве параметра полная энергия частицы Е. В теории дифференциальных уравнений доказывается, что уравнения такого вида, как уравнения Шредингера, имеют решения однозначные, конечные, непрерывные не при любых значениях параметра Е, а лишь при некоторых избранных значениях. Эти значения называются собственными значениями энергии, а соответствующие им решения уравнения Шредингера, называются собственными волновыми функциями.