3.2.6 Линии наибольшего наклона.

Линиями наибольшего наклона плоскости к плоскостям проекции называются прямые, лежащие в плоскости и перпендикулярные к линиям уровня этой плоскости.

На рисунке 21 а) треугольником АВС задана плоскость Р.

В этой плоскости линия A1 является горизонталью, а перпендикулярная горизонтали прямая есть линия небольшого наклона плоскости Р к горизонтальной плоскости проекций. Иначе эта линия ВО называется еще линией ската.

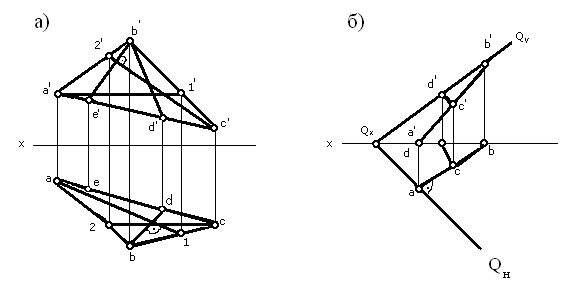
bd  а1 ab  Q_н

b'e a'2' c'd' Q_v

Рисунок 21. Линии наибольшего наклона

Прямая C 2 на этом же рисунке – фронталь, а перпендикулярная к ней линия ВЕ есть линия наибольшего наклона плоскости Р к фронтальной плоскости проекций.

Если плоскость задана следами рисунок 21 б), то построение линий наибольшего наклона облегчается. Известно, что следы – это ”нулевые” линии уровня, т.к. они лежат в плоскостях проекций: горизонтальный след – нулевая горизонталь, а фронтальный след  нулевая фронталь. Прямая АВ, перпендикулярная горизонтальному следу, есть линия ската, и прямая CD, перпендикулярная фронтальному следу – линия наибольшего наклона плоскости Q к фронтальной плоскости проекций.

Линии наибольшего наклона применяются для определения углов наклона плоскости общего положения к плоскостям проекций.

Прямая КВ (рисунок 22) является линией наибольшего наклона плоскости Q к плоскости H (эта линия называется линией ската).

Рисунок 22. Угол наклона плоскости Q к плоскости Н

Как видно из рисунка 22, угол BKb есть линейный угол двугранного угла, образуемого плоскостями Q и Н. КВ  Q_н.

Решение задачи на эпюре показано на рисунке 23.

Рисунок 23. Определение угла наклона плоскости Q к

горизонтальной плоскости проекции H на эпюре

Угол наклона плоскости Q к фронтальной плоскости проекций определяется аналогично с помощью линии наибольшего наклона плоскости проекций.

3.2.7 Пересечение поверхности плоскостью.

3.2.7.1 Пересечение гранной поверхности плоскостью.

Замкнутая плоская фигура, имеющая форму многоугольника, полученная при пересечении гранной поверхности плоскостью, называется сечением. Вершины многоугольника принадлежат рёбрам, а стороны –граням многогранника.

Поэтому задачу определения линий пересечения многогранника плоскостью можно свести к многократному решению задачи по определению линии пересечения двух плоскостей (граней многогранника и секущей плоскости) или к задаче по нахождению точки встречи прямой (рёбер многогранника) с секущей плоскостью. На рисунке 24 дано решение задачи, в которой секущая плоскость  проецирующая, а на рисунке 25 – секущая плоскость общего положения. В этом случае рационально применить для решения какойлибо способ преобразования эпюра.

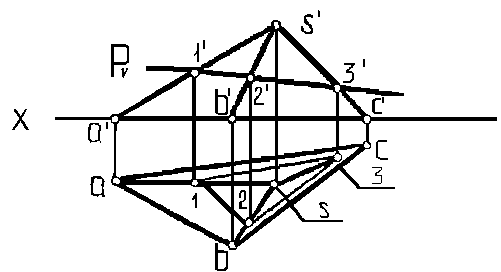
Рисунок 24. Пересечение гранной поверхности проецирующей

плоскостью.

Рисунок 25. Пересечение гранной поверхности плоскостью общего

положения

3.2.7.2 Пересечение поверхностей вращения.

3.2.7.2.1 Пересечение цилиндра плоскостью.

При пересечении цилиндра различными плоскостями в сечении могут получаться окружность (рисунок 26,а), эллипс (рисунок 26,б) и две прямые образующие (рисунок 26,в)

Рисунок 26. Сечение цилиндра плоскостью

3.2.7.2.2 Пересечение конуса плоскостью.

При пересечении конуса различными плоскостями в сечении могут получиться ниже перечисленные линии (рисунок 27):

а) окружность (плоскость Р перпендикулярна оси конуса);

б) эллипс (плоскость Q пересекает все образующие конуса);

в) парабола (плоскость S параллельна одной образующей конуса);

г) гипербола (плоскость Т параллельна двум образующим конуса);

д) две прямые - образующие (плоскость Р проходит через вершину конуса).

Рисунок 27. Сечение конуса плоскостями

На рисунке 28 показано определение линии пересечения конуса с плоскостью общего положения. В результате пересечения получился эллипс. Для построения его воспользовались способом замены плоскостей проекций. На плоскость V₁ секущая плоскость спроецировалась в виде прямой a'₁b'₁ . Отрезок c'₁d'₁ определяет большую ось эллипса. Малая ось ef получена на плоскости Н с помощью окружности радиуса R, которой принадлежат точки e'₁=f '₁.

Рисунок 28. Пересечение конуса плоскостью общего положения

Натуральную величину эллипса можно получить, воспользовавшись любым способом преобразования эпюра либо построив эллипс по двум его осям.