3.2.1 Принадлежность точки и прямой плоскости.

3.2.2.1 Принадлежность точки и прямой линии (рисунок 1). Точка принадлежит прямой линии, если проекции ее лежат на одноименных проекциях прямой.

АВ (аb, a'b');

C  AB;

E  AB;

D  AB

Рисунок 1. Oтносительное положение прямой АВ и точек C D E

3.2.1.2 Точка принадлежит плоскости, если она принадлежит любой прямой, лежащей в этой плоскости (рисунок 2).

а'b'  с'd' аb  сd

 (АВ  CD)

1. М  Е (e' e)

2. e' ∩ а'b' = 1'

3. e ∩ аb = 1

4. e' ∩ c'd' = 2'

5. e ∩ cd = 2

6. m  e

m'  e'

M  E

Рисунок 2. Принадлежность точки М плоскости  (АВ // СD)

3.2.1.3 Прямая лежит в плоскости, если две любые точки прямой принадлежат плоскости (рисунок 3) или одна из точек прямой принадлежит плоскости и данная прямая параллельна какой-либо, заведомо принадлежащей плоскости (рисунок 4).

Рисунок 3. Принадлежность Рисунок 4. Принадлежность

прямой E прямой E

плоскости  ( АВС) плоскости  ( АВС)

3.2.2 Определение натуральной величины (Н.В.) отрезка прямой общего положения и углов наклона (, ) прямой к плоскости проекции Н и V (рисунок 5).

Рисунок 5. Определение натуральной величины отрезка прямой и

углов наклона ее к плоскостям проекций

3.2.3 Взаимное положение двух прямых, прямой и плоскости.

3.2.3.1 Прямые линии могут в пространстве пересекаться между собой, быть параллельными и скрещиваться. У параллельных прямых общего положения их одноименные проекции параллельны (рисунок 6)

Рисунок 6. Параллельные Рисунок 7. Пересекающиеся

прямые прямые

Пересекающиеся прямые имеют одну общую точку. Одноименные проекции пересекающихся прямых в точках, лежащие на одной линии связи (рисунок 7).

Две прямые линии, не параллельные и не пересекающиеся между собой, называются скрещивающимися. Такие прямые не имеют общей точки. Поэтому точки пересечения одноименных проекции скрещивающихся прямых не лежат на одной линии связи (рисунок 8).

В этих точках расположены проекции двух точек, лежащих на разных прямых, но находящихся на одном фронтально или горизонтально проецирующем луче. Такие точки называются конкурирующими, с их помощью определяется видимость на эпюре.

Рисунок 8. Скрещивающиеся прямые

На рисунке 8 точки Е и F фронтальная конкурирующие, причём точка F будет видимой на фронтальной плоскости проекции, т.к

У_F  У_Е. Из двух горизонтально конкурирующих точек Р и Q точка Р видима, т.к Z_Р Z_Q.

3.2.3.2 Взаимное положение двух плоскостей.

Две плоскостей в пространстве могут быть либо параллельными, либо пересекаться между собой. Линия пересечения плоскостей это прямая, одновременно принадлежащая каждой из плоскостей. Строится она путём определения двух любых точек, общих для обеих плоскостей (рисунок 9).

Рисунок 9. Построение линии пересечения двух плоскостей

Рисунок 10  Построение линий пересечения двух не прозрачных

треугольников

3.2.3.3 Параллельные плоскости.

Две плоскости параллельны между собой, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости (рисунок 11).

 (АМ х АN) ║  (ВЕ х ВF)

a'm' ║ b'e'; am ║ be  АМ ║ ВЕ P_V ║ Q_v

  ║   P ║ Q

a'n' ║ b'f'; an ║ bf  AN ║ BF P_н ║ Q_н

Рисунок 11. Параллельные плоскости

3.2.3.4 Взаимное положение прямой и плоскости

Рисунок 12. Наглядное изображение прямой АВ,

пересекающейся с плоскостью Р

Для определения точки пересечения прямой АВ с плоскостью Р необходимо выполнить следующие операции (рисунок 12).

1. Провести через прямую вспомогательную проецирующую

плоскость Q.

2. Построить линия МN пересечения данной плоскости Р с

вспомогательной.

3. Рассмотреть относительные положения прямой АВ и найденной

линии MN.

Возможны три случая:

1) АВ совпадает с MN, тогда АВ принадлежит плоскости Р

(АВ  MN; АВ  P).

2) АВ параллельна MN, тогда АВ параллельна плоскости Р

(АВ║MN; АВ║P).

3) АВ пересекает MN в точке К, которая является точкой пересечения

прямой АВ с плоскостью Р (АВ ∩ MN  К).

АВ  Q; Q  V AB  Q; Q  H;

Q ∩ P = MN; Q ∩ P = MN;

MN ∩ AB = K MN ∩ AB = K

Рисунок 13. Построение точки пересечения прямой АВ с плоскостью

3.2.4 Перпендикулярность геометрических элементов.

3.2.4.1 Проецирование прямого угла.

Прямой угол проецируется на плоскость проекций в натуральную величину в том случае, когда одна сторона прямого угла параллельна этой плоскости проекций, а другая не перпендикулярна к ней (рисунок 14).

АВ║Н; сk  аb DE║V; f 'k '  d'e'

Рисунок 14. Построение прямого угла

3.2.4.2 Прямая перпендикулярна к плоскости, если она перпендикулярна к двум пересекающимся прямым, принадлежащим этой плоскости (рисунок 15). Чтобы прямой угол между этими линиями спроецировался в натуральную величину на обе плоскости проекций, двумя пересекающимися прямыми плоскости должны быть выбраны линии уровня этой плоскости, её горизонталь и фронталь (или профильная прямая). При этом фронтальная проекция перпендикулярна к плоскости должна быть перпендикулярна к фронтальной проекции фронтали (или к фронтальному следу плоскости), а горизонтальная проекция его перпендикулярна к горизонтальной проекции горизонтали (или к горизонтальному следу плоскости) (см. рисунок 15).

а) б)

Рисунок 15. Построение прямой, перпендикулярной к плоскости

а) в пространстве, б) на эпюре

На (рисунке 16, а, б) показано построение перпендикуляра, проведенного из точки D к плоскости  ( ABC) и Q (Q_v x Q_н)

а) б)

Рисунок 16. Построение прямой, перпендикулярной к плоскости

3.2.5 Способы преобразования эпюра.

3.2.5.1 Общие сведения о способах преобразования комплексного

чертежа.

Решение задач позиционного и метрического характера значительно облегчается, если данные элемента располагаются параллельно или перпендикулярна плоскости проекций. Для этого прибегают к построению дополнительных проекций. Построение этих проекции называют преобразованием чертежа.

Такое преобразование может быть выполнено следующими способами:

а) заменой (переменной) плоскостей проекций;

б) вращением (перемещением) геометрического объекта;

в) переменой направления проецирования.

3.2.5.2 Способы замены плоскостей проекций.

При этом способе преобразования эпюра предмет в пространстве остаётся неподвижным, относительно него меняется положение плоскостей проекций. При замене фронтальной плоскости проекций координата Z каждой точки объекта (предмета) остаётся неизменной. При замене горизонтальной плоскости проекции остается без изменения координата Y(рисунок 17, 19)

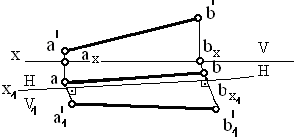
Пример 1. Преобразовать прямую общего положения АВ в линию уровня (рисунки 17).

Чтобы прямая общего положения стала линией уровня, необходимо новую плоскость проекции расположить параллельно прямой, тогда ось проекции в новой системе плоскостей проекций должна быть проведена параллельно одной из проекций прямой. В данном случае прямая АВ преобразована во фронталь.

; ; ; х₁║ab; V₁║АВ

Рисунок 17. Определение натуральной величины прямой

Пример 2. Преобразовать плоскость общего положения в проецирующую (рисунок 18).

На рисунке 18 показаны две задачи, в каждой из которых плоскость общего положения преобразована в проецирующую, для чего в первом случае ось Х₁ проведена перпендикулярно Р_н, а во второй – перпендикулярно горизонтальной проекции горизонтали данной плоскости.

; х₁  Р_н ; ; а'1'║х ; х₁  а₁;

 ( АВС)  V₁

Рисунок 18. Преобразование плоскости общего положения в

проецирующую

Пример 3. Определить натуральную величину  АВС.

Определение натуральной величины треугольника выполняется в два этапа: в первом – плоскость треугольника преобразуется в проецирующую, а во втором – в плоскость уровня. При этом ось Х₁ выбирается перпендикулярно горизонтальной проекции горизонтали треугольника, а ось Х₂ – параллельна проекции a'₁b'₁c'₁, т.е. плоскость треугольника заняла положение плоскости уровня (см. рисунок 19).

1. ; h =   ABC; х₁а₁; 2. ; х₂║ a'₁b'₁c'₁

Рисунок 19. Определение натуральной величины плоскости

общего положения

3 .2.5.3 Вращением вокруг линии уровня треугольник спроецируется в натуральную величину, если плоскость этого треугольника расположить параллельно какой – либо плоскости проекции. Такое преобразование можно выполнить путём вращения треугольника вокруг его линии уровня. Каждая точка треугольника будет перемещаться по окружности, расположенной в плоскости, перпендикулярной к оси вращения (рисунок 20).

Рисунок 20. Вращение плоскости вокруг горизонтали

Горизонтальные проекции точек а и 1 остаются неподвижными, т.к. они лежат на оси вращения. Меняют положение точки b и c , причем обе они перемещаются в горизонтально – проецирующих плоскостях Q и S,перпендикулярных к оси вращения и, следовательно, параллельных между собой. Точка b пересекается по окружности радиуса R, который найден по правилу прямоугольного треугольника. Отложив отрезок ОВ_о на следе Q_н от точки О, нашли повёрнутое положение точки В. Для определения повернутого положения точки С радиус ее вращения можно не находить. Точка С получится при пересечении прямой В₁ со следом плоскости S_н.