3. Положение вершины:

Cлева от оси Oy при < 0, выполняется когда a>0 и b>0, или a<0 и b<0

Справа от оси Oy при >0 , выполняется когда a>0 и b<0, или a<0 and b>0

Выше оси Ox при ( ) >0

Ниже оси Ox при ( ) <0

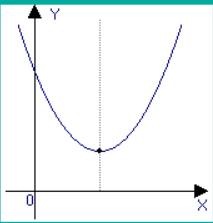
a>0, D>0 a>0, D=0 a>0, D<0

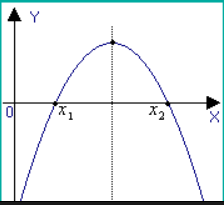
A<0, D>0 a<0, D=0 a<0, D<0

Эти графики для случая, когда >0; при <0 всё так же, но слева от Ox ……………………………………………………………………………………………………………..

• ОБЛАСТЬ ОПРЕДЕЛЕНИЯ: R

• ОБЛАСТЬ ЗНАЧЕНИЙ: при a > 0 [-D/(4a); ) при a < 0 (- ;-D/(4a)]

• ЧЕТНОСТЬ, НЕЧЕТНОСТЬ: при b = 0, то функция четная при b   0, то функция ни четная, ни нечетная

• НУЛИ: при D > 0 два нуля:  при D = 0 один нуль: x₁ = -b/(2a) при D < 0 нулей нет

• ПРОМЕЖУТКИ ЗНАКОПОСТОЯНСТВА: если a > 0, D = 0, то y > 0 при x   (- ;x₁)U(x₁; ) если a > 0, D < 0, то y > 0 при x   R если a < 0, D = 0, то y < 0 при x   (- ;x₁)U(x₁; ) если a < 0, D < 0, то y < 0 при x   R

• ПРОМЕЖУТКИ МОНОТОННОСТИ:

• ЭКСТРЕМУМЫ: при a > 0 x_min = -b/(2a) y_min = -D/(4a) при a < 0 x_max = -b/(2a) y_max = -D/(4a) 

ВОПРОС №27 Необходимые и достаточные условия расположения корней квадратного трёхчлена относительно заданного числа (с выводом).

Данное число располагается между корнями квадратного трехчлена.

Дано:

Необходимое и достаточное условие того, что оба корня квадратного трехчлена больше данного числа.

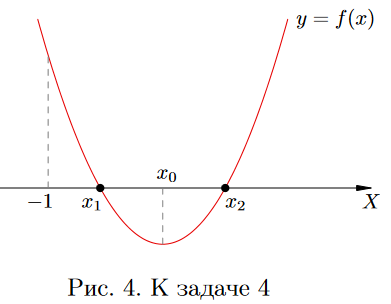
(Далее при доказательстве заменить в тексте и рисунке число -1 переменной t)!!!!!.

(взято с сайта. mathus.ru›Материалы по математике›Трёхчлен Можно посмотреть и скопировать в PDF)

ВСЕ ВАРИАНТЫ ЕСТЬ В ТАБЛИЦЕ №51 Е.П.НЕЛИНА! (нужно просто понять принцип!)

……………………………………………………………………………………………………………

ВОПРОС №28 Определение многочлена. Степень многочлена. Операции сложения и умножения многочленов. Корень многочлена. Деление многочлена на многочлен с остатком (столбиком и методом неопределённых коэффициентов).

 Многочленом (или полиномом) называют выражение вида

a₀xⁿ+a₁x^n-1+a₂x^n-2+...+a_n-2x²+a_n-1x+a_n

Где n - любое натуральное число или 0, a0, a1, ..., an - какие-то действительные числа, называемые коэффициентами многочлена. 

Степенью многочлена называется наибольший показатель степени переменного. Член, содержащий наибольшую степень называется старшим членом многочлена.

Суммой двух многочленов и назовем многочлен

f(x)+f(y) = c0 + c1 + c2 …..+ cn-1x+ cn коэффициенты, которого являются суммой коэффициентов и с равными степенями (приводим подобные слагаемые)

Произведение многочленов. Чтобы умножить многочлен на многочлен, нужно каждый член одного многочлена умножить на каждый член другого многочлена и полученные произведения сложить. (a+b)·(c+d)=a·c+a·d+b·c+b·d.

Отсюда следует, что при умножении многочленов, содержащих m и n членов соответственно, указанная сумма произведений членов будет состоять из m·n слагаемых

Корень многочлена (понятное объяснение см. в учебнике 10кл. стр.60)

Здесь q(x) – частное от деления многочлена f(x) на двучлен (x-c).

Деление многочленов с остатком у Нелина стр. 21, 22 таб.15. (два способа).

Метод неопределённых коэффициентов).

Даны многочлен: P_x(x)=a₀xⁿ+a₁x^n-1+…+a_n-1·x+a_n степени n и T_m(x)=b₀x^m+b₁x^m-1+…+b_m-1·x+b_m степени m

Положим частное q_n-m(x)=x^n-m+c₁x^n-m-1+…+c_n-m (1)

и остаток r_l(x)=d₀x^m-1+d₁x^m-2+…+d_m-1, (2)

где числа c1, c2, …,c_n-m и d₀, …,d_m-1 не определены.

Напишем тождественное равенство

P_n(x)=T_m(x)·q_n-m(x)+r_l(x). (3)

Перемножая многочлены T_m(x) и q_n-m(x) и приводя подобные члены, в правой части равенства (3) получим многочлен n-ой степени, который записывается в каноническом виде. Приравнивая коэффициенты при одинаковых степенях х этого многочлена и многочлена P_n(x), получим систему n уравнений, решая которую находим числа c₁, c₂, …,c_n-m, d₀, d₁,…,d_m-1.

Если окажется, что все числа d₀, d₁, …,d_m-1 равны нулю, то это означает, что многочлен P_n(x) делится нацело на многочлен T_m(x). Если хотя бы один из коэффициентов d_0, d_1, …, d_m-1 отличен от нуля, то многочлен P_n(x) делится на многочлен T_m(x) с остатком, при этом степень остатка l равна максимальной степени одночлена от x правой части (2), при котором коэффициент не равен нулю.

Пример. Разделить многочлен 2x⁴+x³-5x²-x+1 на многочлен x²-x.

Решение. Ищем частное от деления многочленов в виде многочлена q₂(x)=2x²+c₁x+c₂,

а остаток в виде многочлена r₁(x)=d₀x+d₁.

Имеем тождественное равенство 2x⁴+x³-5x²-x+1=(2x²+c₁x+c₂)·(x²-x)+d₀x+d₁.

Раскрывая скобки и приводя подобные члены, получаем 2x⁴+x³-5x²-x+1=2x⁴+(c₁-2)·x³+

(-c₁+c₂)·x²+(d₀-c₂)·x+d₁.

Приравнивая коэффициенты при одинаковых степенях x, имеем систему

c₁-2=1,

-c₁+c₂=-5,

d₀-c₂=-1,

d₁=1,

откуда c₁=3, c₂=-2, d₀=-3, d₁=1.

Следовательно, q₂(x)=2x²+3x-2, а r₁(x)=-3x+1, т.е.

2x⁴+x³-5x²-x+1=(2x²+3x-2)·(x²-x)-3x+1.

Деление многочлена на многочлен столбиком См. учебник 10кл. стр.54 (то, что подчёркнуто и примеры).

……………………………………………………………………………………………………………

ВОПРОС №29 Теорема Безу и её следствия (с доказательством). Схема Горнера (с выводом). Понятие кратности корня многочлена.

Теорема Безу: Остаток R от деления многочлена P(x) на двучлен (x ‑ a) равен значению этого многочлена P(x) при x=a, т.е. R = P(a).

Пусть :

P ( x ) – данный многочлен степени n ,

двучлен ( x - a ) - его делитель,

Q ( x ) – частное от деления P ( x ) на( x – a). Q ( x ) имеет степень n-1.

R – остаток от деления. R-число.

Доказательство:

Согласно правила деления многочленов с остатком можно записать:

P (x) = (x-a)·Q(x) + R .

Отсюда при x = a

P (a) = (a-a)·Q (a) + R =0·Q(a)+R=0+ R = R.

Значит, R = P ( a ) , т.е. остаток от деления многочлена на ( x - a ) равен значению этого многочлена при x = a , что и требовалось доказать .

Следствия из теоремы Безу:

Следствие 1 Число a является корнем многочлена P(x) тогда и только тогда, когда P(x) делится на (x ‑ a) без остатка.

Доказательство:

По теореме Безу остаток от деления многочлена P (x) на (x – a) равен P (a) , а по условию a является корнем P (x) , а это значит , что P (a) = 0 , что и требовалось доказать .

Следствие 2 Если многочлен P(x) имеет попарно различные корни a1, a2 ….. an,

то он делится без остатка на произведение (x- a1) (x- a2) …… (x- an).

(доказывается через мат. индукцию. http://mirznanii.com/a/312686/teorema-bezu

см. следствие3)). И в Виленкине стр.56 (теорема 3)

Следствие 3 Многочлен степени n имеет не более n различных корней.

Доказательство:

Воспользуемся методом от противного: если бы многочлен P( x ) степени n имел бы более n корней – (n + k) (a1 , a2 , … , a(n + k) - его корни ) , тогда бы по ранее доказанному следствию 2 он

бы делился на произведение ( x - a1 ) … ( x – a(n + k) ) , имеющее степень n + k , что невозможно .

Мы пришли к противоречию, значит наше предположение неверно и многочлен степени n не может иметь более, чем n корней , что и требовалось доказать .

ЕСТЬ ЕЩЕ СЛЕДСТВИЯ В ТЕТРАДИ БЕЗ ДОК-ВА!!!!!!!!!

Схема Горнера (с выводом). ( См. учебник 10кл. стр.58).

Теорема. Пусть и . Найдутся многочлен и число такие, что .

Доказательство. Будем искать в виде . Из равенства = при сравнении коэффициентов получаем цепочку равенств: , , , . . . , , , откуда последовательно определяются коэффициенты и остаток :

(Чтобы это понять, нужно начать перемножение и после приведения подобных слагаемых будет видно, откуда бирутся эти коэффициенты)

, ,

,…, ,

.

Теорема доказана. Более того, получен очень удобный способ вычисления коэффициентов и остатка . Этот способ носит название схемы Горнера.

П р и м е р. Найти неполное частное и остаток от деления многочлена на линейный двучлен .

Решение. Составим таблицу:

Понятие кратности корня многочлена.

Определение. Число k называется кратностью корня с в многочлене f(x),если многочлен f(x)= ·Φ(x), где многочлен Φ(x) уже не делится на (x c), а сам корень с k-кратным корнем этого многочлена.

Если k=1, то говорят, что корень с– простой.

……………………………………………………………………………………………………………

ВОПРОС №30 Теоремы о целых и рациональных корнях многочлена с целыми коэффициентами (с доказательством) и их применение (приведите примеры).

Теорема о целых и рациональных корнях многочлена с целыми коэффициентами

Теорема 1. Если все коэффициенты многочлена

f(x)=a₀xⁿ+ a₁x^n-1+ a₂x^n-2+...+ a_n-2x²+ a_n-1x+ a_n   являются целыми числами, то всякий целый корень этого многочлена является делителем свободного члена a_n

Теорема 2. Если многочлен f(x)=a₀xⁿ+ a₁x^n-1+ a₂x^n-2+...+ a_n-2x²+ a_n-1x+ a_n с целыми коэффициентами и со старшим коэффициентом, равным единице, имеет рациональный корень, то этот корень - целое число

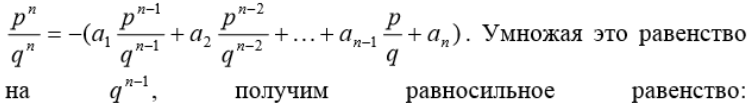
Теорема. Если рациональное число является корнем многочлена F(x) с целыми коэффициентами, то его свободный член делится на p, а старший коэффициент делится на q

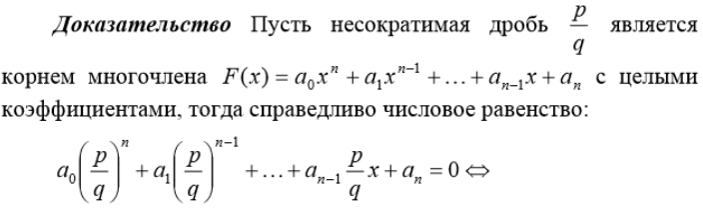
Умножим это равенство на

Возможно, более удобные примеры в учебнике Алгебра10кл., стр. 61.

……………………………………………………………………………………………………….

ВОПРОС №31 Обобщённая теорема Виета (с доказательством) (приведите примеры).

Обобщенная теорема Виета для многочлена n-й степени.

. Формулы Виета —выражают коэффициенты многочлена через его корни.

Формулировка

(приведенный многочлен)x n + a 1 x n − 1 + a 2 x n − 2 + . . . + a n , {\displaystyle x^{n}+a_{1}x^{n-1}+a_{2}x^{n-2}+...+a_{n},}

то коэффициенты a1, a2,…,an по Формулм Виета выражаются таким образом:

Иначе говоря, ·ak равно сумме всех возможных произведений из k корней.

Доказательство

Доказательство осуществляется рассмотрением равенства, полученного разложением многочлена по корням.

Так как a0=1, и c1, c2,…,cn – корни многочлена, имеем тождество:

1.Произведём последовательное перемножение и приведём подобные слагаемые.

2.Сравним коэффициенты при переменных с равными степенями в левой и правой частях тождества.

3.Воспользуемся определением равенства многочленов

a 0 = 1 {\displaystyle a_{0}=1} Если коэффициенты при переменных с равными степенями равны, то многочлены равны.

4.Получаем формулы Виета

Из последней формулы Виета следует, что если корни многочлена целочисленные, то они являются делителями его свободного члена, который также целочисленный.

Если старший коэффициент многочлена a0 ≠ 1 то для применения формул Виета необходимо предварительно разделить все коэффициенты на a0 (см. приведенный многочлен)

Доказательство

Пусть х1; х2… хn – корни многочлена n-ой степени

Р(х) = a₀ xⁿ + a₁ x^n-1 +…+ a_n-1 x + a_n. (неприведенный многочлен)

Тогда его можно разложить на множители

a₀ xⁿ + a₁ x^n-1 +…+ a_n-1 x + a_n = a₀ (x-x1)·(x-x2)·(x-x3)…(x-xn)

Разделим левое и правое выражение на a₀ Выполняя указанные выше действия, получим формулы Виета в общем вид

ВОПРОС №32 Дробно-рациональная функция. Правильные и простейшие рациональные дроби. Теорема о представлении рациональной дроби в виде суммы многочлена и правильной дроби (без доказательства, привести примеры)

Вариант ответа №1

Дробно-рациональная функция (рациональная дробь)

Теорема всякая рациональная дробь представима притом единственным способом, в виде суммы многочлена и правильной дроби.

Вариант ответа №2

Рациональные дроби. Рациональной дробью называется дробь, числителем и зна­менателем которой являются многочлены, т. е. всякая дробь вида

Если степень многочлена в числителе больше или равна степе­ни многочлена в знаменателе ( > ), то дробь называется непра­вильной. Если степень многочлена в числителе меньше степени многочлена в знаменателе ( < ), то дробь называется пра­вильной.

Всякую неправильную рациональную дробь ( , > ) можно представить в виде суммы многочлена (целой части ) и правильной рациональ­ной дроби ,n<m

Это представление достигается путем деления числителя на знаменатель по правилу деления многочленов.

Пример. ,

Так как

ВОПРОС №33 Дробно-рациональная функция. Правильныея и простейшие рациональные дроби. Разложение правильной рациональной дроби в сумму простейших дробей (без доказательства, привести примеры).

Дробно-рациональная функция (рациональная дробь) определяется формулой

где степени n и m – целые числа, n≥0, m≥0,

коэффициенты многочленов – действительные числа, a≠0, b≠0.

Рациональной дробью называется выражение вида ,

где Pn(x), Qm(X), – многочлены степеней n и m соответственно.

Если n<m, рациональная дробь называется правильной, 

в противном случае – n ≥ m – неправильной. (по аналогии с обычной дробью).

Простейшими рациональными дробями называются правильные рациональные дроби следующих четырех типов:

где A, B, C, a, p, q – числа, k N, k 1

Теорема

ВОПРОС №34 Понятие угла между параллельными, пересекающимися и скрещивающимися прямыми. Перпендикулярность прямой и плоскости. Признак перпендикулярности прямой и плоскости (с доказательством).

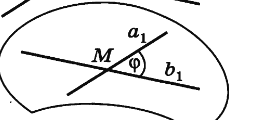
Угол между прямыми в пространстве

Скрещивающиеся прямые

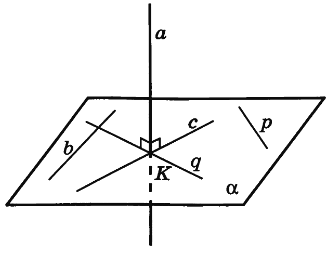
Признак перпендикулярности прямой и плоскости.

(Доказательство теоремы и чертёж – см. учебник «Геометрия 10 класс теорема 13 стр.49-51)

……………………………………………………………………………………………………………..

ВОПРОС №35 Теорема о трёх перпендикулярах (с доказательством).

……………………………………………………………………………………………………………..

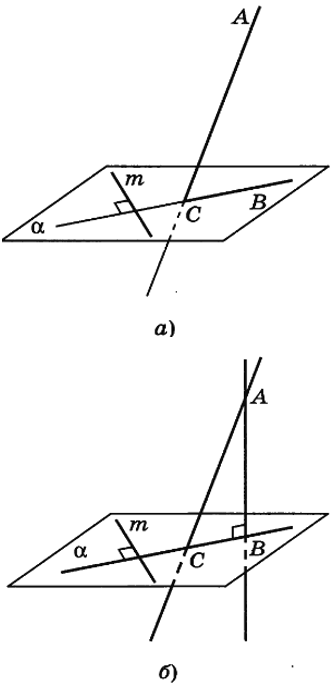ВОПРОС №36 Расстояние между фигурами. Доказательство существования и единственности общего перпендикуляра двух скрещивающихся прямых. Доказательство равенства расстояния между скрещивающимися прямыми длине их общего перпендикуляра.

Расстояние между фигурами. (Геометрия 10кл. стр.97, 98).

Определение. За расстояние между фигурами F1 и F2 принимается наименьшее расстояние между каждой точкой M первой фигуры и каждой точкой N второй фигуры.

Расстояние между фигурами F1 и F2 будем обозначать:

!!!! На этом утверждении выстраиваются доказательства по нахождению наименьшего расстояния между фигурами.

Доказательство существования и единственности общего перпендикуляра двух скрещивающихся прямых. ( Доказательство разобрано в учебнике. Параграф16; стр.83-84. Там же есть и чертёж.)

Определение. Общим перпендикуляром двух скрещивающихся прямых называется отрезок, имеющий концы на данных прямых и перпендикулярный к ним.

Теорема. Две скрещивающиеся прямые имеют общий перпендикуляр, и притом единственный.

Доказательство существования. общего перпендикуляра прямых а и b.

1). Проведем через прямые a и b параллельные плоскости α и β соответственно. Также через прямую a проведем плоскость γ, перпендикулярную плоскости β.

Пусть γ β a1

Тогда a || a1 (т.к “Если плоскость походит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой” (Теорема 10))

a1 b C (пересечение прямых a1 и b есть точка C)

Поскольку прямая a1 является ортогональной проекцией прямой а на плоскость β, то точка С также является ортогональной проекцией некоторой точки A (A a )

Следовательно, AC ⊥ β.

Но, тогда  AC ⊥ b. (Поскольку АС перпендикулярен плоскости β, он перпендикулярен любой прямой, лежащей в этой плоскости) и AC ⊥ a

AC ⊥ a (С – ортогональная проекция точки А). И, поскольку

И, поскольку АС – общий перпендикуляр по определению.

Доказательство единственности общего перпендикуляра прямых а и b.

Допустим, что существует другой общий перпендикуляр прямых а и b, например отрезок А1С1. Тогда дложны выполняться условия:

А1 a и C1 b

А1С1 ⊥ a и А1С1⊥ b

Так как a || a1 и А1С1 ⊥a , то А1С1⊥ a1 (по лемме о перпендикулярности двух параллельных прямых к третьей)

Тогда 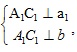 и, следовательно, А1С1⊥β (по признаку перпендикулярности прямой и плоскости).

 Тогда имеем следовательно,

АС || А1С1 (по обратной теореме (№15) “если две прямые перпендикулярны к плоскости, то они параллельны”).

Раз эти прямые параллельны, то точки А, С, А1 и С1 лежат в одной плоскости. А, следовательно, и прямые а и b, которым принадлежат эти точки, лежат в одной плоскости, но это невозможно. Значит, допущение неверно, и общий перпендикуляр скрещивающихся прямых а и b является единственным.

(В приведённом выше доказательстве излишне проводить параллельную пл-ть α через прямую a. Достаточно плоскостей γ β. Видимо, α потребуется для дальнейших рассуждений.)

Доказательство расстояния- позже!!!!!!!

ВОПРОС №37 Доказательство теоремы о площади ортогональной проекции многоугольника.

Параграф17; стр.85-88.

Теорема

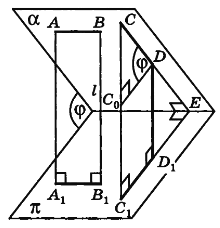
Рис.1 Рис.2 Рис.3

Доказательство 1 (для треугольника).

Пусть есть треугольник ABC и его проекция ABC1 на плоскость α. Проведем высоту CD треугольника ABC. По теореме о трех перпендикулярах отрезок C1D – высота треугольника ABC1. Угол CDC1 равен углу φ между плоскостью треугольника ABC и плоскостью проекции α. 

C1D= CD

SABC = AB·CD, SABC1 = AB·C1D, следовательно

SABC1 = SABC

Следовательно, для треугольника теорема верна

Замечание. Данное док-во справедливо, также, для случая, когда сторона AB треугольника не лежит в пл-ти проекции, но параллельна ей. Так-как

(см рис.3).

Доказательство для многоугольника.Пусть Ф- данный многоугольник ABCD (см. рис.2). Его ортогональную проекцию - многоугольник A1B1C1D1 – обозначим Ф1. Разобьем их на соответственные треугольники.

Каждый треугольник, у которого нет стороны, параллельной плоскости проекции, следует разбить на два треугольника с общей стороной, параллельной плоскости проекции. (см. замечание)

……………………………………………………………………………………………………………

ВОПРОС №38 Двугранный угол. Линейный угол двугранного угла. Угол между плоскостями. Перпендикулярность плоскостей. Признак перпендикулярности плоскостей (с доказательством). Свойства перпендикулярных плоскостей.

Параграф14;15 стр. 75-83.

Определение

Двугранный угол - это часть пространства, заключённая между двумя полуплоскостями, имеющими одну общую границу.

Полуплоскости α и β, образующие двугранный угол, называются его гранями.

Общая прямая a этих граней называется ребром двугранного угла.

Определение

Линейный угол двугранного угла есть пересечение данного двугранного угла и плоскости, перпендикулярной его ребру

Как построить линейный угол двугранного угла?

Теорема. Величина линейного угла не зависит от выбора его вершины на ребре двугранного угла

Угол между плоскостями.

Перпендикулярность плоскостей

Признак перпендикулярности плоскостей

(формулировка следствий не требуется в данном билете)

Свойства перпендикулярных плоскостей.

……………………………………………………………………………………………………………..