2. Теоремы умножения.
Произведение двух четных или двух нечетных функций является четной функцией.
(док-во см. ВИЛЕНКИН стр. 113)
Произведение четной и нечетной функции является нечетной функцией.
(Доказать самостоятельно по аналогии с предыдущими теоремами, используя определение четности-нечетности функций).
3.
Если функция f четна, то и функция 1/f четна
Если функция f нечетна, то и функция 1/f нечетна
…………………………………………………………………………………………………………....
ВОПРОС №12 Определение периодической функции, периода, основного периода функции. Теоремы о периодических функциях. (с доказательством). Примеры.
Разбор темы и примеры см. Е.П. Нелин (зеленая книжка) СТР.37, 38 таб. 29
Определение
Функция f(x) - периодическая, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f(x+T) = f(x).
Период, основной период функции
Число Т называют периодом функции f, если при любом x из области определения выполняются равенства f(x-T)= f(x)=f(x+T).
Основным периодом функции f называется наименьший положительный период этой функции
Теорема о том, что любой период кратен основному
Доказательство.
Предположим противное, то есть что
существует период
функции
f (
>0),
не кратный Т. Тогда, разделив
на
Т с остатком, получим
,
где
.
Поэтому
то есть
–
период функции f, причем
,
а это противоречит тому, что Т– основной
период функции f. Из полученного
противоречия следует утверждение
теоремы. Теорема доказана.
Теорема о связи периода функции y=f(kx+b) с периодом функции y=f(x).
Теорема. Если число T - основной период f(x), то число T/k - основной период для f(kx+b), где k не равно 0.
Доказательство. Пусть Т - основной период f(x), тогда f(x) =f(x+T),
Рассмотрим f(kx+b) = f((kx+b)+T) = f((kx+T)+b) =f(k(x+T/k)+b)
В итоге
=>
-период,
ч.т.д
Теорема о периодичности сложной функции.
Если функция y= f(x) периодическая с периодом Т, то сложная функция
y=f(g(x))-также периодическая с периодом Т.
Дано: y= f(x) и y= g(x)- периодическая функция.
Доказать: y=f(g(x))- периодическая функция.
Доказательство: Если g(x)- периодическая функция, то g(x+T) =g(x) (по определению).
Следовательно, f(g(x+T)) = f(g(x)),
т.о. y=f(g(x))- периодическая функция.
Самостоятельно привести примеры функций. (см. Е.П. Нелин СТР.37, 38, таб. 29).
……………………………………………………………………………………………………………
ВОПРОС №13 Неопределяемые понятия и аксиомы стереометрии. Простейшие следствия из аксиом.
Аксиома 1.
Через любые 3 точки, не лежащие на одной прямой, можно провести плоскость, притом только одну.
Аксиома 2.
Прямая, проходящая через 2 точки плоскости, лежит в этой плоскости.
Аксиома 3.
Если две плоскости имеют одну общую точку, то их пересечение есть прямая, проходящая через эту точку
Следствия.
Через любую прямую и не лежащую на ней точку можно провести плоскость , и притом только одну.
Доказательство: 1) Рассмотрим прямую a и точку A, которая не находится на этой прямой. 2) На прямой a выберем точки B и C. 3) Так как все 3 точки не находятся на одной прямой, из второй аксиомы следует, что через точки A, B и C можно провести одну единственную плоскость α. 4) Точки прямой a, B и C, лежат на плоскости α, поэтому из третьей аксиомы следует, что плоскость проходит через прямую a и, конечно, через точку A.
5)Допустим такая плоскость не одна. Значит существует вторая плоскость y, которая проходит через A, B, C. => они совпадают.
Через две пересекающиеся прямые можно провести плоскость, и притом только одну
Док-во аналогично
Через 2 параллельные прямые можно провести плоскость, и притом только одну
Док-во через определение парал. Прямых.
…………………………………………………………………………………………………………
ВОПРОС №14 Взаимное расположение двух прямых в пространстве. Доказательство признака скрещивающихся прямых.
Для взаимного расположения прямых в пространстве возможен один и только один из трёх случаев
не параллельны и не пересекаются
Признак скрещивающихся прямых
…………………………………………………………………………………………………………………
ВОПРОС №15 Взаимное расположение прямой и плоскости в пространстве. Доказательство признака параллельности прямой и плоскости.
Взаимное расположение прямой и плоскости в пространстве
Прямая может 1. лежать на данной плоскости, 2. пересекать ее в одной точке, или 3. быть параллельна данной плоскости.
Теорема. Признак параллельности прямой и плоскости.
Дано:
a
b;
β;
b⊂β
Доказать: a║β
ВОПРОС №16 Взаимное расположение плоскостей в пространстве. Доказательство теоремы о линии пересечения плоскостей, следствия из теоремы (с доказательством).
Взаимное расположение плоскостей.
Теорема о линии пересечения плоскостей
Следствия из теоремы
1,
Если две прямые параллельны третьей, то они параллельны между собой.
Доказательства этих следствий см. чебник геометрии 10кл., стр. 46, 47.
…………………………………………………………………………………………………………...
ВОПРОС №17 Взаимное расположение плоскостей в пространстве. Теоремы о параллельных плоскостях (с доказательством).
Взаимное расположение плоскостей.
Если каждая из двух пересекающихся прямых одной плоскости параллельна другой плоскости, то данные плоскости параллельны.
Если две пересекающиеся прямые параллельны двум прямым другой плоскости, то эти плоскости параллельны.
Прямые, по которым две параллельные плоскости пересечены третьей плоскостью, параллельны.
Если прямая пересекает одну из двух параллельных плоскостей, то она пересекает и другую.
Если плоскость пересекает одну из двух параллельных плоскостей, то она пересекает и другую плоскость.
Через точку, не лежащую в данной плоскости, можно провести плоскость, параллельную данной, и притом только одну.
Две плоскости, параллельны третьей, параллельны.
Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.
Все теоремы и доказательства к ним см. чебник геометрии 10кл., § 13,
стр. 68, 74. КАКИЕ ТЕОРЕМЫ НУЖНЫ????????
ВОПРОС №23 Линейная функция, её свойства и график. Общее уравнение прямой на плоскости. Признаки параллельности и перпендикулярности прямых на плоскости. Уравнение прямой, проходящей через две заданные точки. Угол между заданными прямыми (с выводом). Пучок прямых.
Всё о линейной функции, ее свойства и график. см. Е.П. Нелин СТР.42, 43, 44 таб. 33. https://fileskachat.com/view/24954_0a6c14138d9255b594208a14beb549d5.html
Линейная функция, её свойства и график. Линейной функцией называется функция вида y = kx + b, заданная на множестве всех действительных чисел. Здесь k – угловой коэффициент (действительное число), b – свободный член (действительное число), x – независимая переменная. В частном случае, если k = 0, получим постоянную функцию y = b, график которой есть прямая, параллельная оси Ox, проходящая через точку с координатами (0; b). Если b = 0, то получим функцию y = kx, которая является прямой пропорциональностью. Геометрический смысл коэффициента b – длина отрезка, который отсекает прямая по оси Oy, считая от начала координат. Геометрический смысл коэффициента k – угол наклона прямой к положительному направлению оси Ox, считается против часовой стрелки. Свойства линейной функции: 1) Область определения линейной функции есть вся вещественная ось; 2) Если k ≠ 0, то область значений линейной функции есть вся вещественная ось. Если k = 0, то область значений линейной функции состоит из числа b; 3) Четность и нечетность линейной функции зависят от значений коэффициентов k и b. a) b ≠ 0, k = 0, следовательно, y = b – четная; b) b = 0, k ≠ 0, следовательно y = kx – нечетная; c) b ≠ 0, k ≠ 0, следовательно y = kx + b – функция общего вида; d) b = 0, k = 0, следовательно y = 0 – как четная, так и нечетная функция. 4) Свойством периодичности линейная функция не обладает; 5) Точки пересечения с осями координат: Ox: y = kx + b = 0, x = -b/k, следовательно (-b/k; 0) – точка пересечения с осью абсцисс. Oy: y = 0k + b = b, следовательно (0; b) – точка пересечения с осью ординат. Замечание.Если b = 0 и k = 0, то функция y = 0 обращается в ноль при любом значении переменной х. Если b ≠ 0 и k = 0, то функция y = b не обращается в ноль ни при каких значениях переменной х.
6) Промежутки знакопостоянства зависят от коэффициента k. a) k > 0; kx + b > 0, kx > -b, x > -b/k. y = kx + b – положительна при x из (-b/k; +∞), y = kx + b – отрицательна при x из (-∞; -b/k). b) k < 0; kx + b < 0, kx < -b, x < -b/k. y = kx + b – положительна при x из (-∞; -b/k), y = kx + b – отрицательна при x из (-b/k; +∞). c) k = 0, b > 0; y = kx + b положительна на всей области определения, k = 0, b < 0; y = kx + b отрицательна на всей области определения. 7) Промежутки монотонности линейной функции зависят от коэффициента k. k > 0, следовательно y = kx + b возрастает на всей области определения, k < 0, следовательно y = kx + b убывает на всей области определения. 8) Графиком линейной функции является прямая. Для построения прямой достаточно знать две точки. Положение прямой на координатной плоскости зависит от значений коэффициентов k и b. Ниже приведена таблица, которая наглядно это иллюстрирует рисунок 1.
Общее уравнение прямой на плоскости
Признаки параллельности и перпендикулярности прямых на плоскости.
Признак параллельности прямых:
A1x + B1y +C1 = 0; A2x + B2y + C2 = 0
A1 / A2 = B1 / B2 != C1 / C2
A1B2 - A2B1 = 0
Признак перпендикулярности прямых:
A1 * A2 / (B1 * B2) = -1
A1 * A2 = -B1 * B2
A1 * A2 + B1 * B2 = 0
Уравнение прямой, проходящей через две точки (с координатами (x1, y1); (x2, y2)
(разбор есть у
Виленкина на стр105, 106. Здесь, наверное,
только
формула нужна)
Угол между заданными прямыми (Вывести формулу для тангенса угла между прямыми).
Итак,
тангенс угла между двумя прямыми
вычисляется по формуле
Пучок прямых
В заданной плоскости γ пучком прямых с центром в точке М0 называют множество всех прямых, лежащих в плоскости γ и проходящих через точку М0.
.....................................................................................................................................................
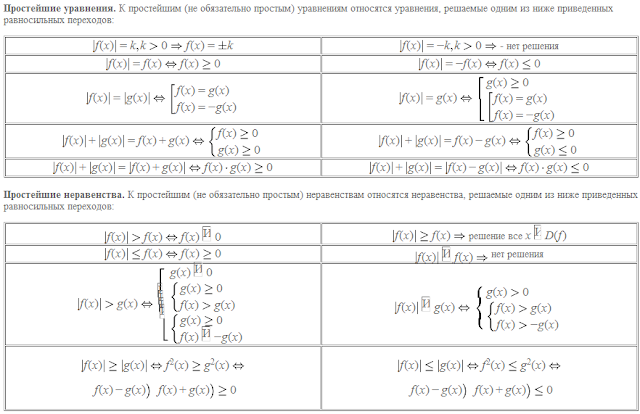
ВОПРОС №24 Кусочно-линейная функция. Понятие модуля числа и модуля выражения. Уравнения и неравенства с модулем, основные равносильные переходы (с доказательством).
Кусочно-линейная функция — функция, определённая на множестве действительных чисел, линейная на каждом из интервалов, составляющих область определения.
пример
кусочно-линейной функции.
Понятие модуля числа и модуля выражения.
Модуль выражения равен самом выражению, если оно неотрицательно, и выражению с противоположным знаком, если оно меньше нуля.
|а·q|
= q·|а|, где q - положительное число
ВОПРОС №25 Квадратичная функция. Выделение полного квадрата. Вывод формулы корней квадратного уравнения, условия их существования и числа. Прямая и обратная теоремы Виета. Разложение квадратного трёхчлена на линейные множители. (с доказательством).
(все подробно в . Е.П. Нелин СТР.46-48 таб. 35). Также учебник 9 класс стр. 35 и далее.
Квадратичной функцией называют функцию вида
,
где
где
a,
b, c –
произвольные
числа, причём
a≠0
Выделение полного квадрата.
Дискриминант представляет некую вспомогательную величину, D = b2 – 4 ac
Вывод формулы корней квадратного уравнения, условия их существования и числа.
D = b2 – 4 ac – дискриминант, тогда
если
D>0
(два корня)
если
D=0
(один корень)
если D<0 уравнение не имеет корней.
Теорема Виета. Сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
Обратная теорема Виета. Если числа m и n таковы, что их сумма равна –p, а произведение равно q, то эти числа являются корнями уравнения x2 + px + q =0
(Доказательство см. учебник алгебры 8 класса стр.198)
Теорема о разложении квадратного трехчлена на линейные множители
Если
x1 и x2 - корни квадратного трехчлена ax2 + bx + c. Тогда этот трехчлен раскладывается на линейные множители следующим образом ax2 + bx + c = a(x - x1) (x - x2).
Доказательство. Подставим вместо
p и q их выражения через x1 и x2 и воспользуемся способом группировки:
x2 + px + q = x2 - (x1 + x2) x + x1 x2 = x2 - x1 x - x2 x + x1 x2 = x (x - x1) - x2 (x - x1) = = (x - x1) (x - x2)
ВОПРОС №26 Свойства и график квадратичной функции. Формулы координат вершины параболы (с выводом). Исследование графика квадратного трёхчлена в зависимости от его коэффициентов
Свойства и график квадратичной функции.(см. разбор на сайте ФизМат http://fizmatinf.blogspot.com/2012/12/25.htm а также Е.П. Нелин СТР.47-48 таб. 35).
Вывод формул координаты вершины параболы
1-способ
Воспользуемся способом выделения полного квадрата. Тогда имеем
Значит
точку
A
вершины параболы можно
получить путём
параллельного переноса графика
вдоль оси
Ox
на
и
вдоль оси Oy
на
,
где D
=
4ac
т.о.
имеем точку A
(
,
).
2-способ
Для определения абсциссы вершины параболы легче рассмотреть случай, когда функция имеет один корень т е при если D=0,
Тогда, используя формулу корней квадратного уравнения,
имеем
Для
нахождения ординаты
достаточно подставить в формулу функции
xₒ
вместо x:
Исследование графика квадратного трёхчлена в зависимости от его коэффициентов.
Направление ветвей. Если a>0 - вверх, a<0 – вниз
Пересечение с осью Oy – точка с координатами (0; c)
(парабола пересекает ось ординат в точке с)