Математические модели входа и выхода.
Дифференциальное уравнение в классической или операторной форме.
ПФ
ОПФ
ЧПФ и другие ЧХ
ВФ
ПХ
Коэффициент передачи
.
Определяется:
если это выражение имеет смысл. (Пример:
коэффициент
передачи отсутствует).Отношение установившейся реакции асимптотически устойчивой системы
на
постоянное воздействие
к
этому воздействию:
Физический смысл чпф.
ЧПФ – частотная передаточная функция: характеризует поведение динамической системы в установившемся режиме при гармоническом входном воздействии и представляет собой комплексную функцию, модуль которой на каждой данной частоте есть отношение амплитуд выходной и входной гармоник, а аргумент равен фазовому сдвигу всех гармоник относительно входной (смотри теорему (7.1).
§8. Частотные и временные характеристики типовых звеньев сау.
Пропорциональное звено
для всех
.
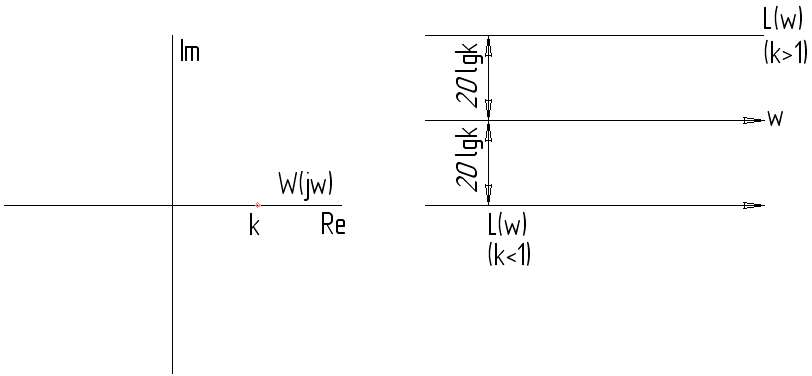
Интегрирующее звено:
Пусть
не
ПФ, а ОПР
.
Пусть размерности входа и выхода
совпадают
но
Поэтому
называется
постоянной времени.
ДУ.
Пусть
Пусть
(ННУ)
Физический смысл постоянной времени интегрирующего звена – она числено, равна времени, по достижении которого значение реакции этого звена на постоянное входное воздействие становится равным этому воздействию.
Пусть
ПХ
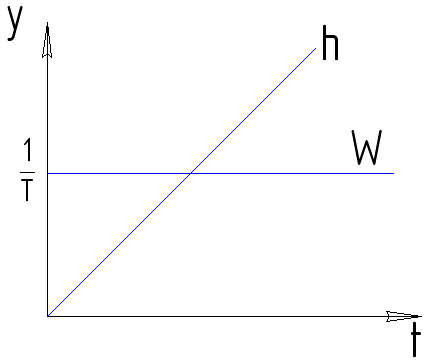
(8.1)
Согласно
(8.1)
.
ЛАХ интегрирующего звена – прямая.
Определим перепад:
перепад
ЛАХ на одну декаду.
.
Следовательно,
коэффициент наклона ЛАХ
(условно:
).
Характерные точки ЛАХ согласно (8.1).
1.
2.
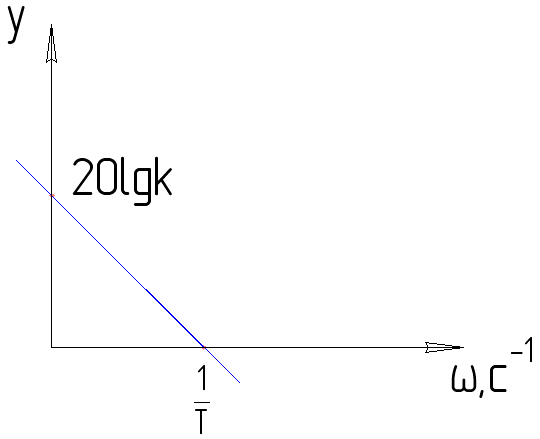
АФХ:
Обобщенное интегрирующее звено
го
порядка.
(8.3)
самостоятельно
представить
в показательной форме (учесть, что
).
Получить выражение для
и
.
Дифференцирующее звено.
Характерные точки для построения ЛАХ – формально те же, что и для интегрирующего звена (смотри (8.2)).
Обобщенное дифференциальное звено.
Апериодическое звено.
постоянная
времени, константа, имеющая размерность
времени
.
Дифференциальные уравнения:
Весовая характеристика.
Для получения АФХ необходимо ЧПФ представить в алгебраической форме (комплексной форме)
|
|
|
0 |
1 |
0 |
|
0.5 |
|
|
0 |
0 |
АФХ
Для получения выражений ЛЧХ в ЧПФ надо выделить модуль и аргумент (представить в показательной форме).
(8.4)
(8.5)
(8.6)
Вместо точной ЛАХ описываемой выражением
(8.5) будем рассматривать асимптотическую
ЛАХ. Она состоит из двух асимптот:
низко-частотной
и высоко-частотной
.
(совпадает с осью частот);
(совпадает с ЛАХ интегрирующего звена
с постоянной времени
).
Асимптоты
и
стремятся в
и
соединяются в точке имеющей абсциссу
сопрягающая
частота. Действительно
,
.
Форсирующее звено.
ЛАХ и ЛФХ этого звена являются зеркальным отображением ЛЧХ апериодического звена относительно оси частот.
Форсирующее звено второго порядка.
Передаточная функция имеет два вещественных полюса, поэтому ПХ имеет периодический характер.
Колебательное звено
,
Полюсы передаточной функции комплексно сопряженные числа, поэтому ПХ характеристика имеет вид колебательного процесса.
ЧПФ:
(8.7)
совпадает
с апериодическим звеном второго порядка.
Сопрягающая частота
Im
АФХ:
Если дана
передаточная функция звена второго
порядка в общем виде
,
то для определения типа звена можно
использовать два способа:
Найти корни знаменателя, если они вещественны, то это апериодическое звено второго порядка. Если комплексные корни, то это колебательное звено.
Представить эту передаточную функцию к стандартной форме передаточного звена. Если
апериодическое
звено второго порядка. Если
колебательное
звено.
Консервативное звено.
,
АФХ:
Re
ЛЧХ:
