§4. Дифференциальные уравнения и передаточные функции линейных систем.

Исходным математическим описанием (МО) системы часто является совокупность уравнений описывающих элементы системы и связи между ними.

В теории АУ используется понятие звена, под которым понимают какой-либо физический элемент системы, либо формально выделенную часть её математической модели, для которой указаны входные и выходная величина. Звено преобразует входные переменные в выходную переменную.

(ДС) – динамическая система определена как математический объект, для которого указаны входные и выходные переменные и существует однонаправленная причинно-следственная связь, это означает, что:

1. выход (следствие) не может появиться раньше (причина).

2. Текущие значения не зависят от будущих.

3. не могут быть изменены в последующей динамической системе.

Математическое описание (ДС) в виде связи входных и выходных переменных называется моделью “вхож выход”. К этим моделям относятся:

1. Передаточные функции

2. Операторная передаточная функция

3. Коэффициент передачи

4. Частотные характеристики

5. Временные характеристики:

• Переходная

• Весовая функция

6. Дифференциальное уравнение

Дифференциальное уравнение линейной непрерывной системы n-го порядка.

(4.1)

n,m – натуральные числа, причём (условие реализуемости); на практике почти всегда (условие строгой реализуемости).

Введём оператор дифференцирования:

; (4.2)

Тогда

Перепишем (4.1) с учётом (4.2)

(4.3)

где полиномы от

Назовём функцию (4.4)

такую, что (4.5)

операторной передаточной функцией (ОПФ).

Выражения (4.4) и (4.5) образуют сокращенную запись дифференциального уравнения (4.3). Эта запись является условной, т.к. не определено, что понимать под операцией деления на операторный полином.

Уравнение (4.1) по Лапласу при нулевых начальных условиях (ННУ)

,

полином от , то , поэтому из (4.1) получаем:

(4.6)

Тогда передаточная функция:

(4.7)

равна (4.8)

Из сравнения (4.4) и (4.8) получаем (4.9)

Вывод: Передаточная функция может быть найдена по ОПФ при помощи формальной замены на . В дальнейшем будем использовать универсальную форму записи

§5. Связь между входом и выходом системы во временной области.

1. Выход может быть найден по известному входу и начальному условию аналитически следующими способами непосредственными решениями дифференциального уравнения (4.1)

2. Методами операционного исчисления (при ННУ)

• 

где

• Нахождение

1. по таблице

2. по формуле разложения Хевинга

3. с помощью интеграла свёртки:

если изображение представляет собой произведение то оригинал может быть найден как: (5.1)

где называется весовой функцией. Оба интеграла в (5.1) называются свёрткой функций и .

Рассмотрим единичную ступенчатую функцию (5.2)

(5.3)

Формально заменим на . Тогда при (5.4)

Рассмотрим функцию

(5.5)

причём (5.6)

Основное свойство функции:

(5.7)

Рассмотрим реакцию системы на функцию при ННУ. Пусть 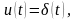тогда по (5.1, 2-ой интеграл)

Вывод: Реакция системы на функцию при (ННУ) совпадает с весовой функцией. Реакция системы на единичное ступенчатое воздействие при (ННУ) – называется переходной характеристикой (ПХ) или переходной функцией (ht). Пусть

(5.1, 1-й интеграл) (5.8)

Отсюда (5.9)

Реакция системы при (ННУ) на функцию:

на ;

на произвольное : см. (5.1).