
UP_Nelineynye_sistemy_upravlenia
.pdf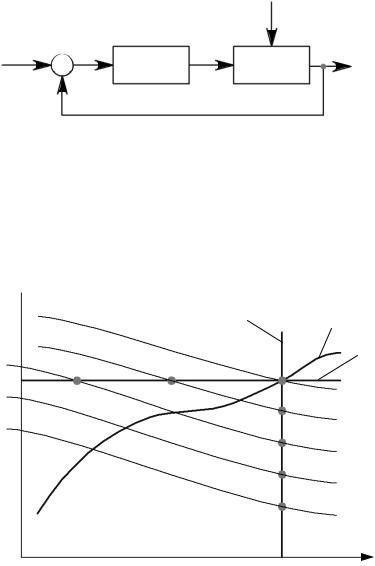
Для приближенной оценки можно оперировать максимальным отклонением выходной величины, соответствующим максимально возможному изменению внешнего воздействия, а также диапазоном изменения крутизны статической характеристики системы, т. е. ее статизма, который в случае нелинейной системы является величиной переменной. Обычно при синтезе систем управления требуется обеспечить статизм меньше заданного в техническом задании.
Для решения этой задачи соответствующей статической характеристикой, компенсирующей характеристику нелинейного элемента, должно обладать управляющее устройство (УУ). Рассмотрим построение статической характеристики управляющего устройства в системе на рис. 4.3.
|
|
|
|
F |
xзад |
u |
x |
||
|
|
УУ |
|
УО |
|
|
|
|
|
Рис. 4.3. Структурная схема системы автоматического управления
Управляемый объект имеет две входные величины – управляющее воздействие u и внешнее возмущение F . Поэтому управляемый объект описывается семейством статических зависимостей x от u , каждая из которых соответствует определенному значению F . Эти зависимости x f u, F могут иметь вид, приведенный на рис. 4.4.
 x
x
1 |
3 |
|
|
|
2 |
x1 |
|
|
F1 |
|
F2 |
|
F3 |
u1 |
u |
Рис. 4.4. Семейство статических характеристик нелинейной системы
61
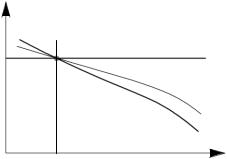
На данном графике показан процесс построения результирующей статической зависимости x от F замкнутой системы по статическим характеристикам объекта и статической характеристике управляющего воздействия (кривая 3). Статическая характеристика управляющего устройства строится в той же системе координат, что и характеристика объекта, только для нее входной величиной является x, а u – выходной величиной.
Точки пересечения характеристик объекта с характеристикой управля-
ющего устройства определяют значения переменных, удовлетворяющие ха- |
||||
|
x |
|
|
рактеристикам обоих звеньев, и, следова- |
|
|
|
|
|
|
|
|
|
тельно, дают значения x и F , по которым |
|
|
2 |
|
может быть построена искомая статиче- |
|
|
|
|
|
|
|
|
|
ская характеристика системы, приведенная |
|
|
3 |
|
на рис. 4.5 (кривая 3). На этом же рисунке |
|
F0 |
1 |
|
показана характеристика объекта при по- |
|
|
|
||
|
|
F |
стоянном u, т. е. при отсутствии управле- |
|
|
|
|
||
Рис. 4.5. Статические характеристики |
ния (кривая 1). Эта кривая соответствует |
|
нелинейной системы |
||
точке пересечения характеристик объекта |
||
|
(рис. 4.4) с вертикальной линией 1, уравнение которой u u1 const . Характеристика 2 системы с управляющим устройством (рис. 4.5) соот-
ветствует характеристике 2 управляющего устройства (рис. 4.4) и получается при увеличении до бесконечности коэффициента передачи управляющего устройства.
Решая обратную задачу, можно, задавшись допустимой величиной статизма, определить характеристику управляемого устройства и найти его требуемый коэффициент передачи.
4.2. Качество нелинейных систем в динамических режимах
Качество переходных процессов в нелинейных системах оценивается теми же известными показателями, что и в линейных системах, т. е. прежде всего временем переходного процесса, максимальным отклонением, колебательностью. Однако в отличие от линейных систем, эти показатели в нелинейных зависят от величины внешнего воздействия, вызвавшего переходный процесс.
Рассмотрим методы определения показателей качества переходных процессов в нелинейных системах. Наиболее простым является случай, когда можно заранее полагать, что входящие в систему нелинейности не оказывают
62
определяющего влияния на динамику системы. В этом случае можно вначале в порядке первого приближения исследовать качество переходных процессов и строить сам процесс, исключив из рассмотрения все нелинейности, и, таким образом, исследовать систему как линейную. Такая ситуация возможна, например, для систем непрерывного действия с насыщением, небольшой зоной нечувствительности, неоднозначной характеристикой с достаточно узкой петлей и т. п.
После проведения такого исследования оценивается влияние неучтенных нелинейностей на динамику системы. Точный учет нелинейностей осуществляется построением переходных процессов с учетом этих нелинейностей. Это, так или иначе, связано с получением решений нелинейных дифференциальных уравнений. К таким методам относятся, например, метод припасовывания, численные методы (Рунге–Кутты), моделирование и др.
Для приближенной оценки влияния нелинейностей можно воспользоваться идеей гармонической линеаризации. Нелинейное звено заменяется гармонически линеаризованным звеном, и принимается, что его передаточная функция остается справедливой в случае произвольной формы входного сигнала. Выразив таким образом параметры передаточной функции через входной сигнал и определив затем, как зависит качество переходных процессов в линейной системе от значений этих параметров, можно качественно определить, как повлияет нелинейность звена на переходные процессы. Например, в случае звена с насыщением такой подход сводится к замене его эквивалентным звеном, коэффициент передачи которого уменьшается с ростом входного сигнала так же, как гармонический коэффициент передачи этого звена уменьшается с увеличением амплитуды входных колебаний.
Чтобы оценить качество процессов в гармонически линеаризованной системе, можно применять показатель колебательности и полосу пропускания как показатель быстродействия. В отличие от линейных систем, здесь вместо одной частотной характеристики получится серия таких характеристик, как функция амплитуды. Соответственно и качество переходных процессов будет зависеть от величины отклонения от установившегося режима.
Для нелинейных систем второго порядка качество переходных процессов полностью определяется по фазовому портрету системы.
63
4.3. Оценка влияния нелинейности на переходные процессы
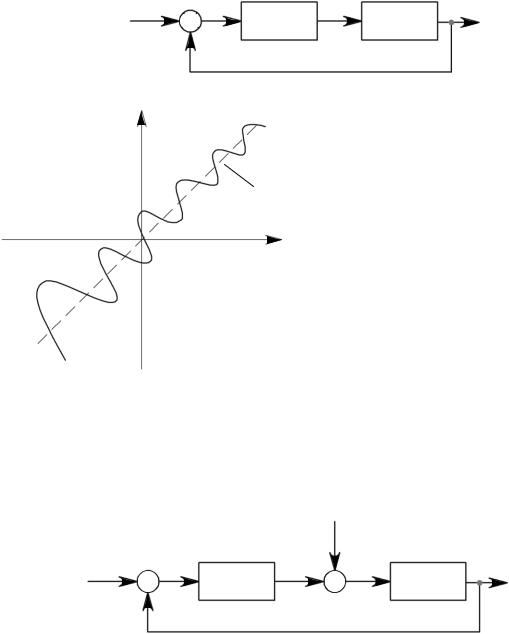
Основная идея рассматриваемого метода заключается в нахождении верхней оценки разницы между переходными процессами в нелинейной системе и переходными процессами в некоторой линейной системе. Линейная система получается из исходной нелинейной системы путем замены нелинейной характеристики на близкую линейную. Рассмотрим нелинейную систему со структурой, показанной на рис. 4.6.
xвх |
|
НЭ |
W(p) |
xвых |
|
|
|
||
|
|
|
|
|
Рис. 4.6. Структурная схема нелинейной системы
z |
Пусть характеристика нелинейного |
|||||||
|
|
|
|
|
|
|
||
|
элемента в рассматриваемой системе |
|||||||
|
имеет вид, приведенный на рис. 4.7. |
|||||||
kx |
Заменим нелинейное звено парал- |
|||||||
|
лельным соединением звеньев с линей- |
|||||||
x |
ной характеристикой zл kx и нели- |
|||||||
|
нейной z z x kx . Обозначим через |
|||||||
|
max |
|
z x kx |
|
. |
При этом линейная |
||
|
|
|
||||||
|
характеристика |
должна |
проводиться |
|||||
Рис. 4.7. Исходная нелинейность |
так, чтобы max |
было минимальным. |
||||||
Тогда структурная схема |
может быть |
|||||||
и близкая линейная аппроксимация |
||||||||
такой, как на рис. 4.8.
Так как система получилась линейной, то к ней применим принцип суперпозиции, причем воздействие ∆z и будет характеризовать влияние нелинейности характеристики.
|
|
|
∆z |
xвх |
|
k |
xвых |
|
|
W(p) |
|
|
|
|
|
Рис. 4.8. Структурная схема линеаризованной системы
Тогда выходное воздействие xвых t xл t x t , где xл t – реакция линейной части системы на задающее воздействие; x t – реакция системы
64
на воздействие ∆z, характеризующее нелинейные свойства системы. Реакцию системы на ∆z можно определить как X p W p z p .
При этом передаточная функция от воздействия ∆z к выходу согласно приведенной структурной схеме (рис. 4.6) рассчитывается следующим образом:
W |
p |
|
|
W p |
. |
(4.1) |
|
|
|
||||
|
1 |
kW p |
|
|||
|
|
|
||||
Для анализа переходных процессов во временной области используется интеграл Дюамеля, для вычисления которого необходимо, используя обратное преобразование Лапласа от передаточной функции (4.1), найти весовую функцию системы
|
|
|
|
|
W p |
|
|
|
|
|
|||||
|
w t L1 |
|
|
|
|
|
|
. |
|
||||||
|
kW p |
|
|||||||||||||
|
|
|
|
1 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Дальше, используя интеграл Дюамеля, можем окончательно найти реак- |
|||||||||||||||
цию системы на возмущающее воздействие ∆z: |
|
|
|
|
|
|
|||||||||
t |
|
|
|
|
t dh |
t |
|
|
|
||||||
x t w t z t d |
|
|
|
|
z t d . |
(4.2) |
|||||||||
dt |
|
|
|||||||||||||
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Для того чтобы оценить влияние возмущающего воздействия, вычислим |
|||||||||||||||
модуль от выражения (4.2): |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
x t |
|
t dh t |
z t d |
|
|
|||||||||
|
|
|
|
||||||||||||
|
|
|
|
|
|
. |
(4.3) |
||||||||
|
dt |
|
|
||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
В (4.3) с учетом введенного ранее обозначения max , |
определяющего |
||||||||||||||
наибольшее отклонение характеристики нелинейного элемента от близкого линейного, можно перейти к неравенству
|
x t |
|
|
t dh t |
|
t |
|
dh |
t |
|
|
||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
||||||||||||
|
|
max |
|
|
|
d |
max |
|
|
|
|
d . |
(4.4) |
||
|
|
dt |
|
|
dt |
||||||||||
|
|
|
|
0 |
|
0 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Сложность нахождения интеграла в (4.4) заключается в том, что необхо- |
|||||||||||||||
димо весь временной интервал от нуля до t разбить на интервалы знакопостоянства, т. е. интервалы времени, на которых dh t 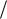 dt 0 и dh t
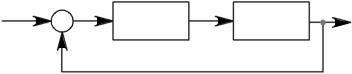
dt 0 и dh t  dt 0 . Тогда интеграл из (4.4) можно будет переписать, например так:
dt 0 . Тогда интеграл из (4.4) можно будет переписать, например так:
65
t |
|
dh t |
|
t1 |
|
dh t |
|
t2 |
|
dh |
t |
|
||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
d |
|
|
|
|
|
d |
|
|
|
|
d |
|
|
|
dt |
|
|
|
dt |
|
|
|
dt |
||||||||
0 |
|
|
|
0 |
|
|
|
t1 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
или, что то же самое,
|
t |
|
|
dh t |
|
|
|
t |
|
|
|
h0 t h1 t |
|
|
|
h1 t h2 |
t |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
d |
h0 |
|
|
|
|
|
|
|
|
. |
|
|||||||||
|
|
|
dt |
|
|
|
|
|
|
|
||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
В итоге, с учетом (4.3) и (4.4) получаем |
|
|
|
|
|
|||||||||||||||||||||
|
x t |
|
max |
|
h0 t |
|
|
|
h0 t h1 t |
|
|
|
h1 t h2 t |
|
. |
(4.5) |
||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||
Выражение (4.5) позволяет оценить реакцию системы на возмущающее воздействие, которое характеризует действие нелинейности на исходную систему.
4.4. Анализ качества процессов методом гармонической линеаризации
Метод гармонической линеаризации можно применить для исследования не только гармонических колебаний, но и колебательных переходных процессов. Для линейных систем косвенными показателями качества являются показатель колебательности, запасы устойчивости по модулю и по фазе, частота среза. Гармоническая линеаризация позволяет с определенной осторожностью использовать эти же показатели и для нелинейных систем. Из всех частотных методов, основанных на гармонической линеаризации, чаще используют метод, основанный на вычислении показателя колебательности.
Рассмотрим линейную систему, в которой нелинейный элемент заменен коэффициентом гармонической линеаризации (рис. 4.9). Такая линеаризация может быть справедлива, если на исходную нелинейную систему действует гармоническое задающее воздействие.
x |
вх |
|
WН(A) |
xвых |
|
|
W(jω) |
||
|
|
|
||
|
|
|
|
|
Рис. 4.9. Структурная схема линеаризованной системы
Согласно принятому ранее допущению, на вход системы подается гармоническое воздействие вида xвх t Asin t .
Тогда частотная передаточная функция замкнутой системы может быть представлена как
66
Wз j , A |
|
Wн A W j |
|
|
. |
|
|
|
(4.6) |
||||||||||
|
Wн A W j |
|
|
|
|||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|||||||||
Коэффициент гармонической линеаризации Wн A удобно представить в |
|||||||||||||||||||
следующем виде: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Wн A NWн0 A , |
|
|
|
|
|
|
|
|
(4.7) |
||||||||
где N – масштабирующий коэффициент; Wн0 A |
– масштабируемая переда- |
||||||||||||||||||
точная функция для значений амплитуды А, изменяющихся от 0 до 1. |
|
||||||||||||||||||
Выражение (4.6) с учетом (4.7) можно преобразовать следующим обра- |
|||||||||||||||||||
зом: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Wз j , A |
|
NWн0 A W |
j |
|
|
|
|
NW j |
|
. |
(4.8) |
||||||||
|
NWн0 |
A W j |
|
|
|
|
|
|
|
|
|||||||||
1 |
W 1 A NW j |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
н0 |
|
|
|
|
|
|
|
|
|
Дополнительно введем обозначение: |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
V |
A W 1 A . |
|
|
|
|
|
|
|
|
(4.9) |
|||||||
|
|
н0 |
|
|
|
|
н0 |
|
|
|
|
|
|
|
|
|
|
|
|
Сделав подстановку (4.9) в (4.8), окончательно получим |
|
|
|||||||||||||||||
Wз j , A |
|
|
|
NW j |
|
|
|
|
|
. |
|
|
(4.10) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
NW j Vн0 |
A |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
Выражение (4.10) позволяет определить показатель колебательности как аналитически, так и графически. Как известно из линейной теории управления, показатель колебательности – это максимальное значение ординаты ам- плитудно-частотной характеристики замкнутой системы при начальной ординате, равной единице:
M |
|
Wз j , A |
|
max |
. |
(4.11) |
|
|
|||||
|
|
|
|
|
|
Наиболее часто показатель колебательности (4.11) для замкнутой системы с передаточной функцией (4.10) находят графически. Для этого на комплексной плоскости в одних осях строятся годографы NW j и Vн0 A , как это показано на рис. 4.10.
67

 jIm
jIm
O Re
|
A |
|
B |
Vн0 |
C |
|
NW j |
Vн0 NW j |
|
Рис. 4.10. Годограф
Числитель передаточной функции замкнутой системы изображается вектором OC , а знаменатель – вектором BC . Если зафиксировать частоту и менять амплитуду А, то максимум модуля частотной передаточной функции будет иметь место при минимальной длине вектора BC .
4.5. Анализ качества по критерию абсолютной устойчивости
Этот критерий может быть использован для оценки качества переходных процессов по степени устойчивости. Основная идея метода заключается в исследовании достижимых условий, при которых затухание вариаций возмущенного и невозмущенного движения происходит быстрее, чем затухание
заданной кривой Me t , где λ – степень устойчивости, определяющая длительность переходного процесса; M – константа, зависящая от величины начального возмущения.
Итак, по принятому условию t xв t xн t Me t . Параметр λ может служить оценкой длительности переходного процесса. Так, для линейных систем можно показать соотношение между временем регулирования и степенью устойчивости tр 3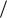 .
.
Для затухания переходного процесса (асимптотической устойчивости) требуется, чтобы
lim |
t lim |
Me t 0 . |
(4.12) |
t |
t |
|
|
|
68 |
|
|

Из (4.12) следует, что
|
lim t e t |
0 . |
|
|||||
|
t |
|
|
|
|
|
||
Умножение оригинала |
t |
|
x |
t x |
t |
|
на экспоненту |
e t влечет за |
|
|
|||||||
|
|
|
в |
н |
|
|
|
|
собой смещение на величину –λ комплексного оператора в передаточной функции линейной части системы. Поэтому критерии абсолютной устойчивости В. М. Попова можно переписать следующим образом:
Re 1 qj Wл j 1k 0 .
Напомним, что это неравенство справедливо для нелинейных систем с устойчивой линейной частью и нелинейностью, удовлетворяющей секторным ограничениям.
Для обеспечения заданной степени устойчивости Wл j должна лежать правее линии, проходящей через точку 1 k ;0 с наклоном 1
k ;0 с наклоном 1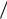 q .
q .
Для определения степени устойчивости некоторой действительной системы нужно построить семейство характеристик Wл j при различных значениях степени устойчивости λ. Степень устойчивости определяется той характеристикой, которая пересекает все прямые Попова с наклоном 1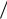 q , кроме одной (1
q , кроме одной (1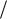 q0 ), с которой она имеет одну или несколько точек касания.
q0 ), с которой она имеет одну или несколько точек касания.
5. КОРРЕКЦИЯ НЕЛИНЕЙНЫХ СИСТЕМ
Цель коррекции – введение в заданную систему дополнительных (корректирующих) устройств для удовлетворения требований, предъявляемых к системе техническим заданием. Коррекция нелинейных систем отличается от коррекции линейных систем тем, что корректирующие устройства в нелинейных системах могут быть как линейными, так и нелинейными.
5.1. Линейная коррекция нелинейных систем
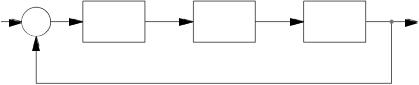
Для достижения требуемой точности и качества процессов управления в нелинейные системы можно вводить линейные корректирующие устройства так же, как и в линейные. Эти линейные корректирующие устройства могут быть последовательными, параллельными и в виде местных обратных связей. Рассмотрим методику синтеза линейных корректирующих устройств для системы, приведенной на рис. 5.1.
69
xвх |
|
ε |
x |
F(p) |
y |
W2(p) |
xвых |
|
|
W1(p) |
|
|
|
Рис. 5.1. Структурная схема нелинейной системы
Пусть характеристика нелинейного элемента F p – нечетная нелинейность с коэффициентом гармонической линеаризации q a . Для простоты будем рассматривать точность и качество процессов около устойчивого равновесного состояния в нулевой точке. Если считать, что q0 a – нормированный коэффициент гармонической линеаризации, а k – коэффициент усиления, то q a kq0 a .
Коэффициент k будем относить к линейной части, поэтому передаточную функцию приведенной линейной части можно записать в виде:
Wp kW p W p .
п1 2
Тогда синтез линейного корректирующего устройства можно осуществить по следующему алгоритму:
строится логарифмическая амплитудно-частотная характеристика линейной части систем:
L |
20lg W |
p 20lg kW |
p W p ; |
неск |
п |
1 |
2 |
формируется желаемая логарифмическая амплитудно-частотная характеристика согласно методикам, известным для линейных систем;
синтезируется линейное корректирующее устройство методами линейной теории;
строится фазочастотная характеристика скорректированной системы;
для данной нелинейности с использованием нормированного коэффициента гармонической линеаризации q0 a строится «запретная зона», со-
ответствующая желаемому показателю колебательности.
Последний пункт алгоритма является дополнительным по отношению к известным методикам синтеза линейных систем. Запретная зона строится в той же системе координат, что и фазочастотная характеристика. Эта зона определяет область, в которую не должна заходить фазочастотная характеристика скорректированной линейной части системы. Запретная зона представляет собой семейство линий M const, где M – показатель колебательности для данной нелинейности. Для корректируемой системы касательная ФЧХ
70
