UP_Nelineynye_sistemy_upravlenia

УДК 681.511.4 (07)

ББК З965.5я7 Б89

Бруслиновский Б. В., Доброскок Н. А., Морозов А. В.

Б89 Нелинейные системы управления: учеб. пособие. СПб.: Изд-во СПбГЭТУ «ЛЭТИ», 2017. 88 с.

ISBN 978-5-7629-1987-6

Содержит основные положения теории нелинейных систем управления. Приведены примеры расчета автоматических систем управления.

Предназначено для студентов, обучающихся по направлению 27.03.04 «Управление в технических системах». Также может быть полезно инженер- но-техническим работникам.

УДК 681.511.4 (07)

ББК З965.5я7

Рецензенты: кафедра электромеханических комплексов и систем

Бруслиновский Борис Васильевич, Доброскок Никита Александрович, Морозов Антон Владимирович

Нелинейные системы управления

Учебное пособие

Редактор Н. В. Кузнецова

_______________________________________________________________________________________________________________________________________________________________________________________________ __________________________________________

Подписано в печать 29.09.17. Формат 60×84 1/16. Бумага офсетная. Печать цифровая. Печ. л. 5,5.

Гарнитура «Times New Roman». Тираж 83 экз. Заказ 000.

__________________________________________________________________

Издательство СПбГЭТУ «ЛЭТИ» 197376, С.-Петербург, ул. Проф. Попова, 5

1. ОБЩИЕ ПОНЯТИЯ О НЕЛИНЕЙНЫХ АВТОМАТИЧЕСКИХ СИСТЕМАХ

Как известно, в общем случае процессы в автоматических системах описываются нелинейными дифференциальными уравнениями.

Несмотря на это, в пределах малых отклонений от номинального режима динамика процессов в автоматических системах с достаточным качеством и степенью точности может быть описана линейными дифференциальными уравнениями. Такой переход от сложной математической модели к более простой возможен, если выполнить линеаризацию нелинейных дифференциальных уравнений в окрестностях выбранного балансировочного режима.

Однако использование для разработок простых моделей не всегда возможно и не всегда оправданно, так как при таком переходе можно получить ошибочные результаты. Это обстоятельство вызвано тем, что практически все автоматические системы в своем составе содержат элементы и функциональные устройства с нелинейными характеристиками, которые не всегда можно линеаризовать даже в окрестностях малых отклонений.

По происхождению элементы и устройства с нелинейными характеристиками, или, сокращенно, нелинейности, в автоматических системах бывают двух видов – непреднамеренные и преднамеренные. К непреднамеренным нелинейностям относятся реальные элементы автоматических систем, характеристики которых нелинейны в силу физических законов, на которых основан их принцип действия. К преднамеренным нелинейностям относятся элементы с нелинейными характеристиками, специально введенные для корректировки системы с целью придания ей особых свойств, которые невозможно получить с элементами с линейными характеристиками.

Для лучшего понимания сути вопроса рассмотрим примеры нелинейных систем.

Пример системы с непреднамеренной нелинейностью. На рис. 1.1

приведена функциональная схема системы регулирования напряжения генератора постоянного тока. В системе применен пропорциональный регулятор выходного напряжения генератора, управляющее воздействие которого – приращение тока возбуждения iв K U , где K – коэффициент передачи регулятора, а U U0 UГ – отклонение напряжения генератора UГ от заданного U0 . Реализация пропорционального закона регулирования в рассматриваемой системе осуществляется с помощью технических устройств,

3

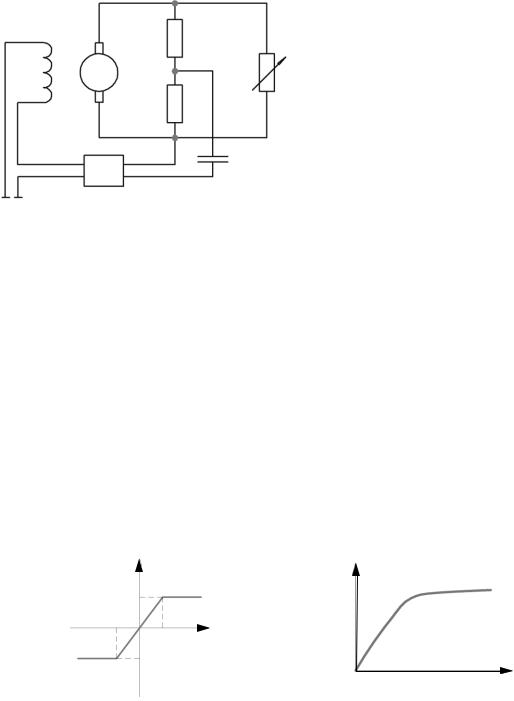
имеющих свои характеристики «вход-выход». Так, например, заданное значение U0 формируется источником постоянного напряжения, в качестве которого может быть применен аккумулятор. Выходное напряжение генератора масштабируется резистивным делителем напряжения таким образом, чтобы U0 и UГ были соизмеримы. Оба устройства можно считать элементами с ли-

ваться как линейная только в ограниченном диапазоне изменения входного напряжения. В действительности выходное напряжение усилителя любого типа – электрического, электронного и т. д. – не может превышать напряжение источника питания, поэтому характеристика реального усилителя является нелинейной, так как, начиная с некоторого значения входного сигнала, его рост не приводит к пропорциональному росту выходного напряжения: выходное напряжение остается неизменным, усилитель входит в режим насыщения. Внешний вид идеализированной характеристики реального усилителя приведен на рис. 1.2, а.

Рис. 1.2. Характеристики нелинейных элементов: а – усилителя; б – генератора постоянного тока

4

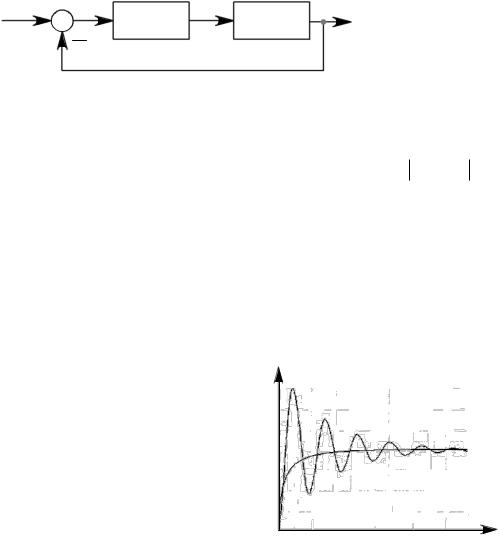
Вторым устройством с нелинейной характеристикой в рассматриваемой системе регулирования является генератор постоянного тока. Его регулировочная характеристика – зависимость выходного напряжения от тока возбуждения – определяется кривой намагничивания стали, что отражено на рис. 1.2, б.

Пример системы с преднамеренной нелинейностью. Рассмотрим ли-

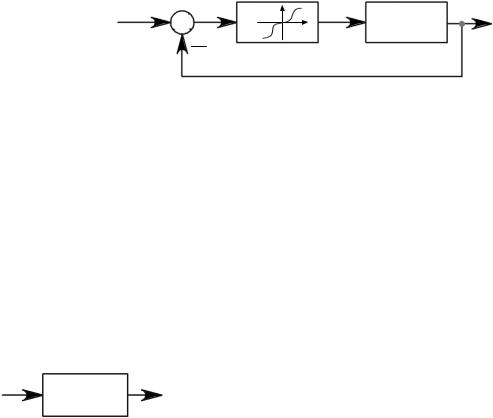
нейную систему регулирования, структурная схема которой приведена на рис. 1.3.

Рис. 1.3. Линейная система регулирования

Исследуем влияние коэффициента передачи системы K на характер изменения рассогласования ɛ(t) при отработке единичного ступенчатого воздействия при условии, что система статическая, устойчивая и WЛ j 1. Как следует из теории линейных систем, характер переходного процесса зависит от K, а именно: чем больше K, тем быстрее нарастает переходная характеристика, тем сильнее колебательный процесс, и наоборот, чем меньше K, тем медленнее нарастает переходный процесс и тем менее он будет колебательным. На рис. 1.4 приведены графики изменения рассогласования при двух различных значениях коэффициента передачи системы K.

Поставим задачу: достичь минимального времени нарастания переходной характеристики при минимальных колебаниях за время регулирования.

В рамках линейной коррекции, т. е. с помощью линейных корректирующих устройств, эту задачу решить затруднительно. Ее

можно решить путем преднамеренного ввода нелинейных корректирующих устройств. Одно из возможных решений задачи показано на

рис. 1.5. Нелинейное звено должно иметь такую статическую характеристику, которая обеспечивает большой коэффициент передачи при больших отклонениях, и малый коэффициент передачи при малых отклонениях, когда система подходит к установившемуся состоянию.

5

WЛ(p)

Рис. 1.5. Коррекция нелинейным устройством

При проектировании систем управления необходимо решать две противоположные по смыслу задачи:

ослабление влияния непреднамеренной нелинейности;

коррекция систем преднамеренными нелинейностями.

И в том и в другом случае необходимо знать соответствующие методы анализа и синтеза нелинейных систем.

1.1.Типовые нелинейности систем управления

Всистемах управления встречаются нелинейности самого различного

вида. Будем характеризовать каждый нелинейный

как это показано на рис. 1.6. Функция z x является статической характеристикой нелинейности. Статические характеристики нелинейностей имеют ряд об-

щих свойств: симметричность, гладкость и однозначность.

Для симметричных характеристик с четной симметрией справедливо тождество φ(x) = φ(–x), для симметричных характеристик с нечетной симметрией – тождество φ(x) = –φ(–x).

Для гладких нелинейностей существует dz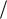dx для любых значений входного сигнала х. Такая нелинейность может быть линеаризована при любых значениях х и z, поэтому такую нелинейность считают аналитической.

Характеристика считается существенно-нелинейной, если есть такие точки, где dzdx не определена.

Для однозначных характеристик любому значению входного сигнала х соответствует единственное значение выходного сигнала z. В противном случае характеристика считается неоднозначной.

Некоторые наиболее часто встречающиеся в системах управления нелинейные элементы принято считать типовыми. Характеристики основных типовых нелинейностей приведены на рис. 1.7 и 1.8.

6

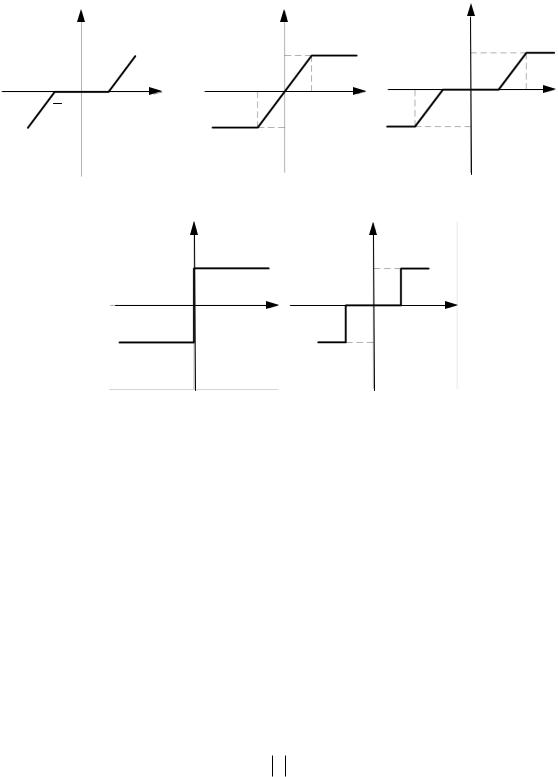
Рис. 1.7. Однозначные типовые нелинейности: а – зона нечувствительности;

б– насыщение; в – зона нечувствительности с насыщением; г – реле;

д– реле с зоной нечувствительности

Нелинейностью, характеристика которой обладает зоной нечувствительности (см. рис. 1.7, а), обладают усилители сигналов, электродвигатели и др. У элементов с зоной нечувствительности в пределах некоторой зоны изменение входного сигнала около нулевого значения не приводит к изменению выходного сигнала. Данная характеристика является существеннонелинейной, так как в точках x xa не существует производная dzdx . Кроме того, характеристика нечетно симметричная и однозначная. Аналитическое описание звена с зоной нечувствительности может быть представлено через кусочно-линейную аппроксимацию следующего вида:

k x xa , x xa , z 0, x xa ,

k x xa , x xa ,

где k определяется через угол наклона линейно возрастающей части зависимости, а xa – порог чувствительности.

Звено с насыщением (ограничением) приведено на рис. 1.7, б. Такую характеристику имеет большинство элементов реальных систем управления,

7

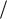
когда при возрастании входного сигнала выходной сигнал не изменяется, достигнув предельного или граничного значения. Насыщение вызывается ограниченностью физических возможностей элементов систем при преобразованиях сигналов. Эти ограничения могут быть по мощности, напряжениям и токам, линейным и угловым перемещениям и т. д. Характеристика является существенно-нелинейной, так как в точках x xa не существует производная dz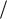dx . Кроме того, характеристика нечетно-симметричная и однозначная. Аналитическое описание звена с насыщением может быть представлено через кусочно-линейную аппроксимацию следующего вида:

где k = za/xa.

Звено с зоной нечувствительности с насыщением показано на рис. 1.7, в. Характеристика данного звена является комбинацией двух предыдущих характеристик нелинейных звеньев. Такую характеристику имеют, например, реальные усилители сигналов, когда в зоне слабых сигналов выходной сигнал отсутствует, а при высоком уровне усиливаемых сигналов усилитель находится в режиме насыщения. Характеристика является существеннонелинейной, так как в четырех точках x xa и x xb не определена производная dzdx . Характеристика нечетно-симметричная и однозначная. Аналитическое описание звена может быть представлено через кусочнолинейную аппроксимацию следующего вида:

Двухпозиционное релейное звено приведено на рис. 1.7, г. Релейной характеристикой на две позиции – «включено-выключено» – обладают элементы систем, основным режимом работы которых является ключевой режим. К таким элементам относятся электромагнитные реле, контакторы, выключатели и переключатели электрических цепей, полупроводниковые ключи с двумя режимами работы (насыщение или отсечка), логические элементы и др. Характеристика является существенно-нелинейной, так, при x 0 не существует производная dz dx . В этой точке значение выходного сигнала не

8

определено. Аналитическое описание звена может быть представлено через функцию z zasign x , где za – величина полки релейного элемента.

Релейное звено с зоной нечувствительности, или трехпозиционное реле, приведено на рис. 1.7, д. Такую характеристику имеют релейные элементы с тремя устойчивыми состояниями. В качестве примера можно привести поляризованное электромагнитное реле, состояние которого зависит от наличия сигнала на входе и его полярности. Если управляющий сигнал отсутствует или меньше некоторого граничного значения, то реле находится в нулевом состоянии. Два других состояния определяются полярностью входного управляющего сигнала. Характеристика является существенно-нелинейной, так как в двух точках x xa не существует производная dzdx . Аналитическое описание звена может быть представлено через функцию

Приведем характеристики нелинейных элементов с неоднозначными характеристиками (рис. 1.8).

mxa xa

–za

Рис. 1.8. Неоднозначные типовые нелинейности:

а – гистерезис; б – трехпозиционное реле с гистерезисом; в – люфт

Характеристика звена с гистерезисом приведена на рис. 1.8, а. Такой характеристикой обладают все реальные элементы и устройства, принцип действия которых основан на перемагничивании ферромагнитных сердечников. Аналитическое описание для нелинейностей с неоднозначными характеристиками отличается от введенных ранее. Выход этих звеньев зависит не только от текущего значения входа, но и от предыстории и начального состояния:

9

Характеристика трехпозиционного реле с гистерезисом приведена на рис. 1.8, б. Такой характеристикой обладают электромагнитные устройства с ферромагнитным сердечником, выходной сигнал которых имеет три дискретных состояния. Характеристика является существенно-нелинейной, так как в четырех точках x xa и x mxa не существует производная dz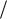dx . Характеристика нечетно-симметричная и многозначная.

Характеристика элемента типа «люфт» приведена на рис. 1.8, в. Такую характеристику имеют механические устройства, где передача осуществляется путем зацепления подвижных частей друг с другом, при этом между этими частями имеется зазор, или люфт. Характеристика является существеннонелинейной, так как во многих точках не существует производная dzdx . Характеристика нечетно-симметричная и неоднозначная.

Приведенные нелинейности могут быть обобщены в класс кусочнолинейных аппроксимаций нелинейных нечетных функций.

К нелинейным звеньям также относятся устройства, выполняющие некоторые математические операции – умножение, деление, вычисление логарифма и т. д.

1.2. Типовые структуры нелинейных автоматических систем

Отметим некоторые принципиальные особенности нелинейных систем. Эти особенности вытекают из того обстоятельства, что процессы в них описываются нелинейными дифференциальными уравнениями. Единой теории нелинейных дифференциальных уравнений не существует. Для нахождения решений нелинейного уравнения фактически создается своя теория. Поэтому возможности анализа нелинейных систем ограничены, что в свою очередь накладывает ограничения на изучаемые структуры нелинейных систем и их математические модели.

10