4.3. Содержание отчета

1.Титульный лист.

2.Цель работы.

3.Расчетные схемы согласно варианту, выполненные в Matlab Simulink.

4.ЛАХ для линейной части системы.

5.Значения амплитуды вибрации и траектории движения выходной переменной для каждой исследуемой нелинейности и системы без учета нелинейности.

7.Выводы.

5.4.Контрольные вопросы

1.Для каких систем применим метод вибрационной линеаризации?

2.Какую форму должно иметь вибрационное воздействие?

3.Где на практике применяется данный метод линеаризации:

4.Какие ограничения накладываются на вибрационное воздействие?

5.Для каких нелинейностей применима вибрационная линеаризация?

ЛАБОРАТОРНАЯ РАБОТА № 5: ИССЛЕДОВАНИЕ ФАЗОВЫХ ТРАЕКТОРИЙ РЕЛЕЙНОЙ СИСТЕМЫ

Цель работы: исследование фазовых траекторий релейных систем с различными типами релейных характеристик.

5.1. Общие сведения

Релейные системы автоматического управления относятся к классу систем дискретного действия, поскольку выходная величина релейного элемента представляет собой дискретный сигнал и изменяется во времени скачками.

15

Преобразование релейным элементом непрерывного входного сигнала в дискретный называется квантованием по уровню.

Большинство релейных систем автоматического управления имеют структуру, приведенную на рис. 5.1. Однако возможны и более сложные системы автоматического управления, содержащие несколько релейных элементов, разделенных частями непрерывного действия.

Рис. 5.1. Релейная система автоматического управления

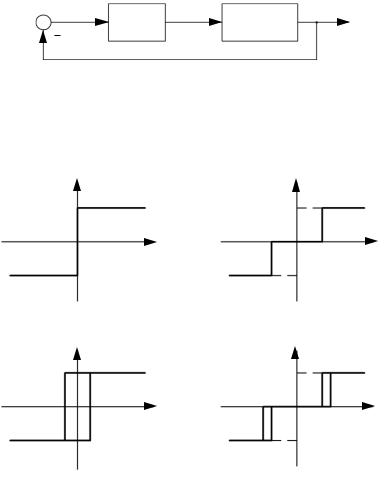
Релейный элемент – это звено релейного действия, статическая характеристика которого может иметь вид одной из характеристик, приведенных на рис. 5.2. Кроме того, релейная характеристика может быть несимметричной.

Рис. 5.2. Статические характеристики релейных элементов: а – двухпозиционное реле; б – трехпозиционное реле; в – гистерезис; г – трехпозиционное реле с гистерезисом

Релейной характеристикой могут обладать такие элементы системы автоматического управления как: реле (электрическое, пневматическое и т. д.), двигатель постоянной скорости (управляемый только командами «включен», «выключен» и, возможно, «реверс»), чувствительное звено релейного действия, полупроводниковые ключи с двумя устойчивыми режимами и др. При этом функционально элемент системы управления с релейной характеристикой может быть как звеном управляющего устройства – чувствительным, усилительным, исполнительным –, так и входить в состав объекта управле-

16

ния. Основное применение в релейных системах получили двух- и трехпозиционные релейные элементы, как с гистерезисом, так и без гистерезиса.

Звенья с релейными характеристиками часто применяются при проектировании автопилотов самолетов, систем управления космическими объектами, авторулевых судов и т. д. Кроме того, релейными характеристиками обладают многие современные системы управления электрическими машинами, в которых питание осуществляется от полупроводниковых преобразователей электрической энергии. Основными достоинствами релейных систем автоматического управления являются их простота, связанная с ней высокая надежность, а также экономичность в расходе энергии питания. При этом релейные системы позволяют осуществлять максимальное быстродействие.

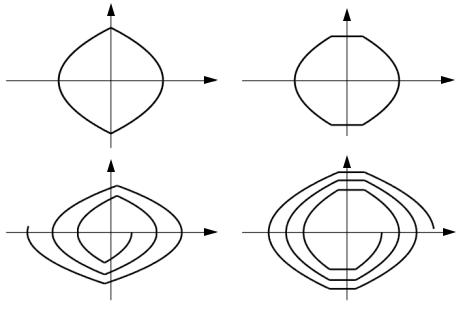
В работе исследуется влияние релейных элементов с различной характеристикой на фазовые траектории и динамику системы автоматического управления. Возможный вид фазовых траекторий системы (см. рис. 5.1) с объектом управления второго порядка приведен на рис. 5.3.

Рис. 5.3. Фазовые траектории системы второго порядка с: а – двухпозиционным реле; б – трехпозиционным реле; в – гистерезисом; г – трехпозиционным реле с гистерезисом

Для релейных систем характерны некоторые особенности динамики. Так, например, в системах с двухпозиционным релейным элементом с одной стороны отсутствует статический режим, с другой стороны существует возможность получения эффекта вибрационной линеаризации. В системах с трехпозиционным реле благодаря наличию зоны нечувствительности принципиально возможен режим покоя без автоколебаний.

17

Как видно из рис. 5.3, вид фазовых траекторий системы зависит от типа релейного элемента. Двухпозиционному реле и трехпозиционному реле соответствует замкнутая траектория. В случае появления гистерезиса изображающая точка бесконечно удаляется от начала координат, что говорит о неустойчивости положения равновесия.

5.2.Порядок выполнения работы

1.Создать новую модель в Matlab Simulink: New Simulink Model

2.Во вкладке Configuration Parameters/Solver задать следующие настройки расчета переходных процессов: type – fixed step; step size – 1e–4.

3.Собрать четыре расчетные схемы, соответствующие структурной схеме, приведенной на рис. 5.1, согласно варианту из таблицы вариантов, с каждым из нелинейных элементов, приведенном на рис. 5.2.

4.Исследовать движение фазовых координат во времени посредством моделирования процессов в системе при отклонении системы от состояния равновесия. Для этого в окне Function Block Parametrs выходного интегратора задать начальное значение: Initial condition, равное единице.

5.Представить результаты исследования схем в виде графиков движения выходной координаты и ее производной во времени и фазовые траектории систем.

5.3. Содержание отчета

1.Титульный лист.

2.Цель работы.

3.Расчетные схемы согласно варианту, выполненные в Matlab Simulink.

18