Релеевский закон распределения
Осуществим генерацию псевдослучайной последовательности, соответствующей релеевскому закону распределения. Одним из способов выполнения данной операции является вызов функции raylrnd().
Нижеприведенные инструкции позволят смоделировать требуемую выборку и вывести её график на экран:
% ввод параметров
sigma=4.359;
N=300; % объём массива
rayl_f3=raylrnd(sigma, N, 1); % моделирование СВ релеевский ЗР
figure(1);
plot(rayl_f3);
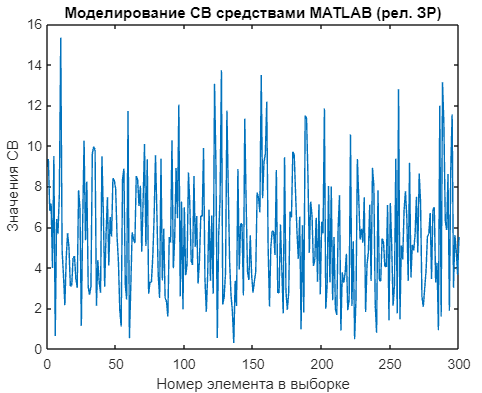
title('Моделирование СВ средствами MATLAB (рел. ЗР)');
xlabel('Номер элемента в выборке');
ylabel('Значения СВ');
Распределение значений выборки наглядно отображено на рисунке 21.
|
Рисунок 21 - График распределения СВ, сформированной с помощью raylrnd() |
В качестве второго метода моделирования массива случайной величины воспользуемся специальными математическими формулами. Программные выкладки, подходящие для среды MATLAB, имеют следующий вид:
% ввод параметров
sigma=4.359;
N=300; % объём массива
a=rand(1,N); % сгенерировать a размерностью N
rayl_f4= sigma*sqrt((-2)*log(a));
figure(2);
plot(rayl_f4);
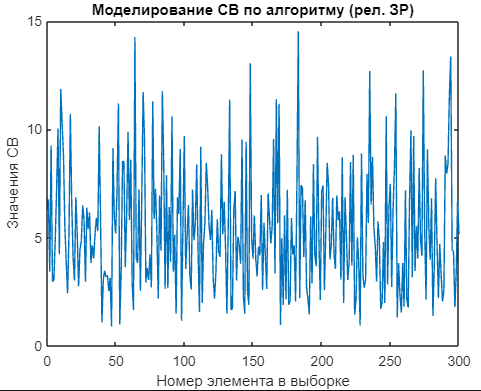
title('Моделирование СВ по алгоритму (рел. ЗР)');
xlabel('Номер элемента в выборке');
ylabel('Значения СВ');
График выборки случайной величины, заданной аналитическими выражениями, показан на рисунке 22.
|
Рисунок 22 - График распределения СВ, сформированной алгоритмически (релеев. ЗР) |
Для полноценного исследования сгенерированной последовательности построим её функцию плотности вероятности и сопутствующую гистограмму. Реализуем данную задачу следующим образом:
N=300; % объём массива
[kol_Y4 Y4]=hist(rayl_f4,50);
p4=kol_Y4/N;
figure(3);
plot(Y4,p4); % построение графика функции
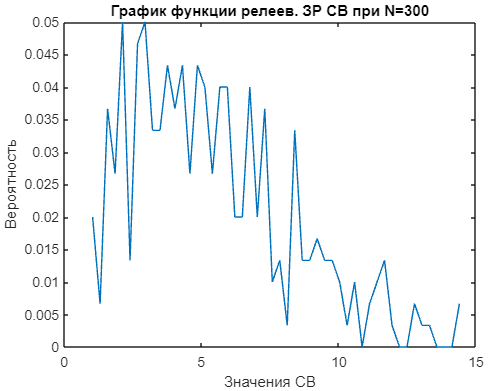
title('График функции релеев. ЗР СВ при N=300');
xlabel('Значения СВ');
ylabel('Вероятность');
figure(4);
histfit(rayl_f4,50,'kernel'); % построение гистограммы
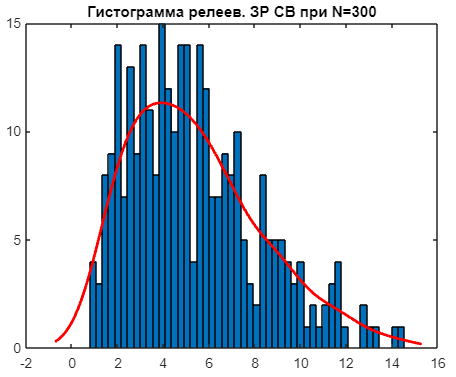
title('Гистограмма релеев. ЗР СВ при N=300');
На рисунках 23-24 отображены образованные кривая и гистограмма функции релеевского закона распределения.
|
|
Рисунок 23 - График функции релеевского закона распределения смоделированной выборки |
Рисунок 24 - Гистограмма функции релеевского закона распределения смоделированной выборки |
Найдём значения таких параметров массива случайной величины, как: математическое ожидание, дисперсия, коэффициент асимметрии и коэффициент эксцесса. В приложении MATLAB для определения каждой из перечисленных величин разработана специальная функция. Применим их, как представлено далее:
rayl_mx1 = mean (rayl_f4); % математическое ожидание средствами MATLAB
rayl_d1= (std(rayl_f4))^2; % дисперсия средствами MATLAB
rayl_as1= skewness(rayl_f4); % коэффициент асимметрии средствами MATLAB
rayl_ex1= kurtosis(rayl_f4); % коэффициент эксцесса средствами MATLAB
Проверим найденные программно характеристики путём повторного вычисления по математическим формулам.
Запишем в Script-файл следующие инструкции:
N=300; % объём массива
rayl_mx2=sum(rayl_f4)/N; % математическое ожидание по алгоритму
rayl_d2=sum((rayl_f4-rayl_mx2).^2)/N; % дисперсия по алгоритму
rayl_as2=sum((rayl_f4-rayl_mx2).^3)/(N*(sqrt(rayl_d2))^3); % коэффициент асимметрии по алгоритму
rayl_ex2=(sum((rayl_f4-rayl_mx2).^4)/(N*(sqrt(rayl_d2))^4))-3; % коэффициент эксцесса по алгоритму
Сравнить вычисленные показатели можно в таблице 4.
Таблица 4 - Параметры выборки СВ, распределенной по релеевскому закону (N=300) |
||
Характеристика |
Вычисления средствами MATLAB |
Вычисления по алгоритму |
Математическое ожидание |
5.3766 |
5.2415 |
Дисперсия |
8.1335 |
7.98 |
Коэффициент асимметрии |
0.7473 |
0.7182 |
Коэффициент эксцесса |
3.1042 |
3.2107 |