Экспоненциальный закон распределения
Выполним вычисление значений функции плотности вероятности экспоненциального закона путём применения функции exppdf(). В качестве входных параметров для данной команды служат: вектор x, математический параметр lambda.
Запишем в программе MATLAB следующий программный код:
% ввод параметров
lambda=3.8;
x=0:0.1:20; % диапазон значений случайной величины
exp_f1=exppdf(x,lambda); % плотность вероятности экспоненциального ЗР
figure(1);
plot(x, exp_f1); % построение графика функции
xlabel('Значения СВ');
ylabel('Вероятность');
title('Функция плотности вероятности экспоненциального закона');
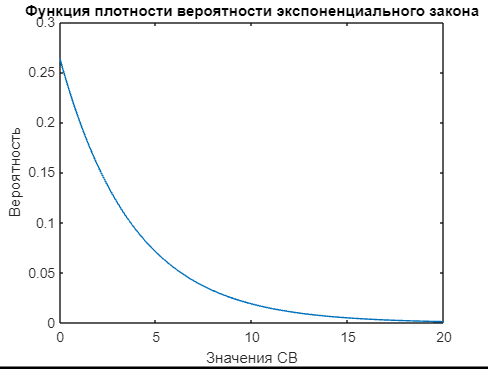
С помощью оператора plot() построим график рассчитанной функции плотности вероятности. На рисунке 5 продемонстрирован внешний вид полученной зависимости.
|
Рисунок 5 - График функции плотности вероятности при экспоненциальном законе |
Чтобы определить значения функции распределения вероятностей показательного закона, обратимся к инструкции expcdf(). Последующее отображение найденных величин осуществим за счет использования команды plot().
Разработанная программная реализация содержит следующий набор операторов:
% ввод параметров
lambda=3.8;
x=0:0.1:20; % диапазон значений случайной величины
exp_f2=expcdf(x, lambda); % распределение вероятностей экспоненциального ЗР
figure(2);
plot(x, exp_f2); % построение графика функции
xlabel('Значения СВ');
ylabel('Вероятность');
title('Функция распределения вероятностей экспоненциального закона');
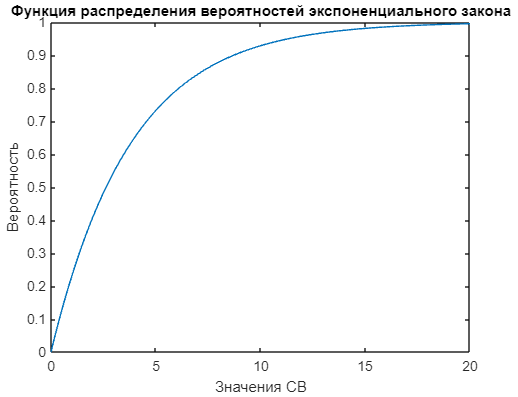
Визуальное представление функции распределения вероятностей приведено на рисунке 6.
|
Рисунок 6 - График функции распределения вероятностей при экспоненциальном законе |
Релеевский закон распределения
Выполним вычисление значений функции плотности вероятности релеевского закона путём применения функции raylpdf(). В качестве входных параметров для данной команды служат: вектор x, среднее квадратическое отклонение sigma.
Запишем в программе MATLAB следующий программный код:
% ввод параметров
sigma=4.359;
x=0:0.1:20; % диапазон значений случайной величины
rayl_f1=raylpdf(x,sigma); % плотность вероятности для ЗР Релея
figure(1);
plot(x, rayl_f1); % построение графика функции
xlabel('Значения СВ');
ylabel('Вероятность');
title('Функция плотности вероятности релеевского закона');
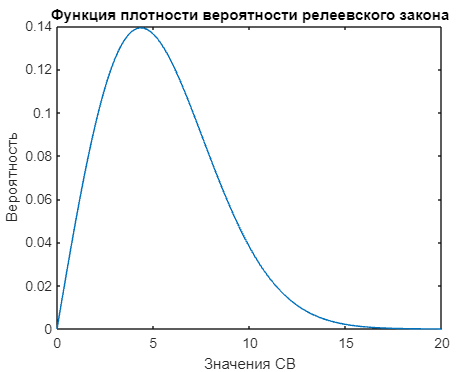
С помощью оператора plot() построим график рассчитанной функции плотности вероятности. На рисунке 7 продемонстрирован внешний вид полученной зависимости.
|
Рисунок 7 - График функции плотности вероятности при релеевском законе |
Чтобы определить значения функции распределения вероятностей релеевского закона, обратимся к инструкции raylcdf(). Последующее отображение найденных величин осуществим за счет использования команды plot().
Разработанная программная реализация содержит следующий набор операторов:
% ввод параметров
sigma=4.359;
x=0:0.1:20; % диапазон значений случайной величины
rayl_f2=raylcdf(x, sigma); % распределение вероятностей ЗР Релея
figure(2);
plot(x, rayl_f2); % построение графика функции
xlabel('Значения СВ');
ylabel('Вероятность');
title('Функция распределения вероятностей релеевского закона');
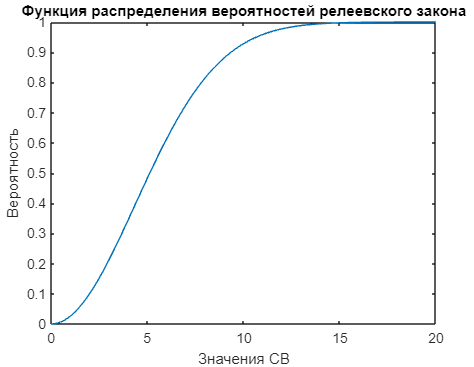
Визуальное представление функции распределения вероятностей приведено на рисунке 8.
|
Рисунок 8 - График функции распределения вероятностей при релеевском законе |
