МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное автономное образовательное учреждение высшего образования

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»

ИНСТИТУТ НЕПРЕРЫВНОГО И ДИСТАНЦИОННОГО ОБРАЗОВАНИЯ

Кафедра прикладной информатики

ОЦЕНКА

ПРЕПОДАВАТЕЛЬ

старший преподаватель _________________ А.В. Сорокин

подпись, дата

ЛАБОРАТОРНАЯ РАБОТА №3

Моделирование случайных величин с заданным законом распределения Вариант 19

по дисциплине «Моделирование»

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ ГР. Z9411 __________________ А.С. Чурилов

подпись, дата

Студенческий билет № 2019/3684

Санкт-Петербург 2023г.

Оглавление

Постановка задачи 3

Исходные данные 4

Основные определения и аналитические выражения 5

Расчет функций плотности вероятности и функций распределения 8

1. Нормальный закон распределения 8

2. Равномерный закон распределения 10

3. Экспоненциальный закон распределения 12

4. Релеевский закон распределения 14

Моделирование случайной величины 17

1. Нормальный закон распределения 17

2. Равномерный закон распределения 20

3. Экспоненциальный закон распределения 24

4. Релеевский закон распределения 28

Вычисление параметров для выборки СВ 33

1. Нормальный закон распределения 33

2. Равномерный закон распределения 34

3. Экспоненциальный закон распределения 35

4. Релеевский закон распределения 37

Ответы на контрольные вопросы 39

Заключение 42

Постановка задачи

Цели лабораторной работы:

• ознакомление с возможностями средств Excel и MATLAB по изучению основных законов распределений (ЗР) одномерных случайных величин (СВ);

• исследование зависимости графиков функций распределения и функций плотности вероятности от параметров распределений;

• изучение возможностей пакетов Excel и MATLAB по моделированию и анализу одномерных случайных величин.

Исходные данные

Параметры для варианта №19:

– для нормального распределения N(m, σ), где (σ > 0):

• математическое ожидание m = 19;

• среднее квадратическое отклонение σ = 4.359;

– для равномерного распределения R(a, b), где (a < b):

• левая граница промежутка a = 19;

• правая граница промежутка b = 38;

– для экспоненциального распределения E(λ), где (λ > 0):

• специальный параметр λ = 3.8;

- для релеевского распределения F(σ), где (σ > 0):

• среднее квадратическое отклонение σ = 4.359.

Основные определения и аналитические выражения

Случайная величина - переменная, которая в результате испытания в зависимости от случая принимает одно из возможного множества своих значений.

Закон распределения случайной величины - всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.

Функцией распределения случайной величины Х называется функция F(x), выражающая для каждого х вероятность того, что случайная величина Х примет значение, меньшее х: F(x) = P (X < x).

Плотностью вероятности (плотностью распределения или просто плотностью) p(х) непрерывной случайной величины Х называется производная ее функции распределения p(х) = F’(x).

Математическое ожидание — понятие в теории вероятностей, означающее среднее (взвешенное по вероятностям возможных значений) значение случайной величины. Общий вид формулы:

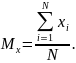
Дисперсия случайной величины — мера разброса значений случайной величины относительно её математического ожидания. Общий вид формулы:

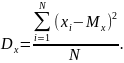
Коэффициент асимметрии —величина, характеризующая асимметрию распределения данной случайной величины. Числовая характеристика случайной величины, равная отношению центрального момента третьего порядка к кубу среднеквадратического отклонения. Общий вид формулы:

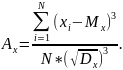
Коэффициент эксцесса — мера остроты пика распределения случайной величины. Общий вид формулы:

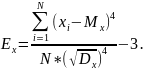
Непрерывная случайная величина Х имеет нормальный закон распределения (закон Гаусса), если ее плотность вероятности имеет вид:

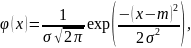
где параметр m — математическое ожидание, параметр σ — среднеквадратическое отклонение распределения, σ ² — дисперсия.

Аналитическое выражение для моделирования случайной величины, распределенной по нормальному закону, имеет вид:

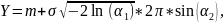
где α₁ и α₂ - независимые равномерно распределенные случайные числа на интервале [0; 1), m – математическое ожидание, σ – среднеквадратическое отклонение.

Непрерывная случайная величина Х имеет равномерный закон распределения на отрезке [a,b], если ее плотность вероятности 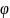(х) постоянна на этом отрезке и равна нулю вне его:

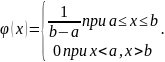
Аналитическое выражение для моделирования случайной величины, распределенной по равномерному закону, имеет вид:

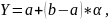
где α - независимые равномерно распределенные случайные величины на интервале [0; 1).

Непрерывная случайная величина Х имеет показательный (экспоненциальный) закон распределения с параметром λ, если ее плотность вероятности имеет вид:

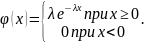
Аналитическое выражение для моделирования случайной величины, распределенной по экспоненциальному закону, имеет вид:

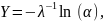
где α - независимые равномерно распределенные случайные величины на интервале [0; 1), 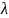– специальный параметр.

Непрерывная случайная величина Х имеет релеевский закон распределения с параметром σ, если ее плотность вероятности имеет вид:

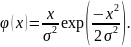
Аналитическое выражение для моделирования случайной величины, распределенной по релеевскому закону, имеет вид:

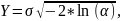
где α - независимые равномерно распределенные случайные величины на интервале [0; 1), 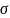– среднее квадратическое отклонение.