5.3. Центробежная сила инерции

Рассмотрим диск, вращающийся вокруг перпендикулярной к нему вертикальной оси z с угловой скоростью(рис. 5.4, а).Вместе с диском вращается надетый на спицу шарик, соединенный с центром диска пружиной. Шарик занимает на спице такое положение, при котором сила натяжения пружины F оказывается равной произведению массы шарика m на его ускорение a_n =²R (R – расстояние от шарика до центра диска, см. (1.30):

F=m²R. (5.8)

Относительно системы отсчета, связанной с диском, шарик покоится, Это можно формально объяснить тем, что, кроме силы (5.6), на шарик действует сила инерции, равная (5.4), но противоположно направленная ускорениюa_n вдоль радиуса от центра дискаF_in=m²R..

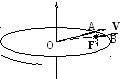
а б

Рис. 5.4 . Рис. 5.5.

Силу инерции, возникающую во вращающейся (по отношению к инерциальным системам) системе отсчета, называют центробежной силой инерции.Эта сила действует на тело во вращающейся системе отсчета, независимо от того, покоится тело в этой системе (как мы предполагали до сих пор) или движется относительно нее.

При точном решении задач о движении тел относительно земной поверхности нужно учитывать центробежную силу инерции. Наблюдаемое относительно Земли ускорение свободного падения тел g обусловлено действием силы тяжести, с которой тело притягивается Землей, и силы центробежной, рис. 5.4, б. Результирующая сил и будет силой тяжестиmg.

Отличие силы тяжести от силы притяжения к Земле невелико, так как центробежная сила инерции значительно меньше,чем сила притяжения к Земле. Так, для массы в 1 кг наибольшее значение центробежной силы, наблюдаемое на экваторе, равно0,035 Н, в то время как сила притяжения равна приблизительно 9,8 Н, т. е. почти в 300 раз больше.

5.4. Сила Кориолиса

При движении тела относительно вращающейся системы отсчета, кроме центробежной силы инерции, появляется еще одна сила, называемая силой Кориолиса или кориолисовой силой инерции.

Появление кориолисовой силы можно обнаружить на следующем примере. Возьмем горизонтально расположенный диск, который может вращаться вокруг вертикальной оси. Прочертим на диске радиальную прямую ОА (рис. 5.5). Запустим в направлении от центра диска шарик со скоростьюv. Если диск не вращается, шарик будет катиться вдоль прочерченной нами прямой. Если же диск привести во вращение в направлении, указанном стрелкой, то шарик будет катиться по изображенной пунктиром кривой ОВ, причем его скорость относительно дискаvбудет изменять свое направление. Следовательно, по отношению к вращающейся системе отсчета шарик ведет себя так, как если бы на него действовала силаF_К, перпендикулярная к скоростиv.Чтобы заставить шарик катиться по вращающемуся диску вдоль радиальной прямой, нужно сделать направляющую, например,в виде ребра. При качении шарика направляющее ребро действует на него с некоторой силой F_r. Относительно вращающейся системы (диска) шарик движется с постоянной по направлению скоростью. Это можно формально объяснить тем, что силаF_rуравновешивается приложенной к шарику силой инерцииF_K, перпендикулярной к скорости v. Сила F_К и есть Кориолисова сила инерции. Можно показать, что модуль ее равен 2mv, а для силы или в общем случае справедливо выражение:

F= 2m[v]. (5.9)

При v= 0 эта сила, в отличие от силы центробежной,отсутствует.