
Методичка ЛР_МоСисУп
.pdfсистеммале |
”ий островоЦыпкинбезгЯ.Заничном. -- известныйане |
|
|
|
|
|
ученый]. |
|
ным |
|
|
тами |
|||||||||||||||||||||
илиописыва мые: |
|
|
д |
|
проц |
ссов |
|
советский |
. |
|
перем |
|
|
|
|||||||||||||||||||
- ели4.1.1ейными. |
|
|
й ых |
|
|
|
|
|
|
|
|
ных си темах |
жеизменениюза служитсят |
||||||||||||||||||||
пк эффициестоязнаТакомные[академиквремтацининарностиветствующ. .) синциальнымиво. враль ого. Это |
|
госто тельсавнения.привОн дит |
|||||||||||||||||||||||||||||||
Л |
|
На пра тике чаще встречаются САУ, которые им |
|
|
|
ат ческие модели, |
|
||||||||||||||||||||||||||
ей ая |
САУ |
азывает |
|
естациоуравнениямиой ес |
|
|
|
её параметрыкоэффиц( |
|
|
|||||||||||||||||||||||
установившременихуравнениктеристичВ числе:тличиегоОсобегичня коепредполояннуравеймиприыхжикоэь,любь,емычтокачонарныхотнелпахвоами,входныхс перногостем,женейдиффобладающемедныхыеозд ренцйствбудутпр .зьессов,висетьныктуСАУистичесавнениявсехараеёимсвойства.ристиютм ты, |
|||||||||||||||||||||||||||||||||
|
Най |
|
его |
|
рни |
|
ни |
оцен |
ть этогоч |
|
|
сть |
неста |
|
|
|
|
САУ практ |
|
|
|||||||||||||
евозм |
|
|
|
дажеустойчивоссист |
|
|
п рядка. |
|
|
|
|
|
|
|
|
|
ационарнойСАУ по кор ямчески |
||||||||||||||||
|
П э |
|
|
|
ин |
|
|
|
пытаюменяютсявторого |
|
ойствах |
|
|
|
|
|
|
||||||||||||||||
называемогжно формальног |
хара теристическогоуравнения, получаемого обычным |
|
|
||||||||||||||||||||||||||||||
формальны |
|
путем (заменой |
|
ка |
ереренциальнвания |
|
|
пер |
|
ром p=d/dt) из |
|
|
|
||||||||||||||||||||
соответствующег |
|
|
|
|
|
2&&&x |
4 tx&& 2 t |
|
. |
|
|
|
|
3x 4 t |
3 y 6 y |
|
|
|
|||||||||||||||
Н пример, для |
|
|
|
|
|
|
x& |
|
|
|
|
|
|||||||||||||||||||||
формальное характ рис |
ческое уравнениеениямеет вид |
|
|
3 |
0 |
|
естационарной |
|
|||||||||||||||||||||||||
Уравнение (2) |
|
|
|
|
в |
|
|
2риближp 4 tpиистационарсудить2 t p |
|
|
|||||||||||||||||||||||
САУ, если |
егокоэффициентыср внительно |
|
|
|
|
меняютсясвойствахвремени. Для этого |
|
|
|||||||||||||||||||||||||
используется |
метод |
позволяедифференциальногоенных коэ фицимедленнотов. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Данный |
|
|
|
|
|
первомдвух вариантах: |
|
|
|
параметрами; |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
“заморажиспользуетсявзнание”судитьпостоянными |
|
. |
|
|
|
(1)2 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||

|
веде |
|
САУ |
|
|
|
|
|
врем |
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
ер а, |
|
|
ч м |
|
|
|
при |
|
|
|
|
|
|
|
|
|
|
|
|
замо аживании |
||||||||||||||||||||||||
|
эфф |
ентов. Од |
ко при |
|
|
|
ьном изменении парам |
|
ров |
|
|
|
|
метполномда огут |
|
|
|
водить |
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
С |
4стема.1.2. Осавтоматбеннсостояниячести прог цессовпралееможнейныхазываетСАУ |
елин йной, если |
стеме |
сод ржитс |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
хотя бы |
|
|
|
|
|
|
|
|
|
ый эл |
|
нт |
|
|
|
|
|
приводит |
|
|
общем случае или к |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
дифференциальномуых |
ур |
внениюалгебраичСАУНа .кихтруктурурав |
|
|
|
|
|
|
схилимах к |
|
|
единомуели ейные нелинейнэл ме ты |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
проявляют |
|
|
свойства, |
|
|
|
|
|
еще |
|
дна |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
них нельзя |
|||||||||||||||||||||||
г |
Таким образ |
|
|
выявля |
|
|
|
|
|
|
|
|
|
|
ность нестационарных САУ: |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
ворить об ус |
|
йчив |
|
|
|
|
|
|
ц лом, |
|
|
|
|
|
|
|
|
говорить лишьоба |
|
|
|
|
|
|
|
|
|
ости отдельн |
|
|
|||||||||||||||||||||||||||||||||||||||
к |
мпонент ве |
|
ра |
|
Схема |
|
|
или векторавыхода. |
|
|
|
|
|
|
|
|
|
де, |
|
как |
|
|
это |
|
представ |
|
йному |
||||||||||||||||||||||||||||||||||||||||||
|
Рису одк |
|
1 |
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
изображ ются |
, |
|
|
|
|
|
|
|
|
|
|
х |
|||||||||||||||||||||||||||||||||||||||
|
нел |
ейного элеме та |
|
|
|
|
|
рисункеИз-1, гдена ич- |
|
|
не |
|
|
|
|
|
|
- выхэ емдустойчинтов нел . |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
начальнымГлавноеусловиямиз их завнешнключается |
мущособтемахвходно. Проя ля |
|
|
|
ся этоти |
сигналылич |
|
|
|
САУ |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
период |
|
ких |
режимов |
|
- |
авт |
|
|
|
|
еб ний, |
|
|
|
|
кже |
|
|
|
вл |
|
ян |
|
|
|
|
|
|
еш их |
|
воз |
|
ущен |
|
|
|
|
||||||||||||||||||||||||||||||||
устойч вочесть |
нелинейной |
|
|
|
|
|
|
. Э |
|
|
явелиения |
|
|
|
|
|
|
|
х САУ отсутствуют |
|
ка |
|
|
ковые. |
х |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из-за |
|
|
|
|
бенно |
|
|
|
|
|
|
нел ней |
|
|
|
х |
|
систем |
|
|
для |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
фаз |
|
|
|
вания |
|
было |
|
|
|
|
ено |
|
п |
|
|
|
|
|
|
|
|
та |
|
|
|
|
азываем |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
го |
|
|
прострлинейных. |
Обычно |
|
|
это |
|
|
|
|
пространство, |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ор |
|
|
|
тами |
|
(фаз |
|
ми) |
|
|
ительного |
|
|
|
|
|
ляются |
|
|
|
|
|
|
|
|
|
|
|
к |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
п рялед |
к САУ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ства |
|
- |
|
|||||||||||||||
|
|
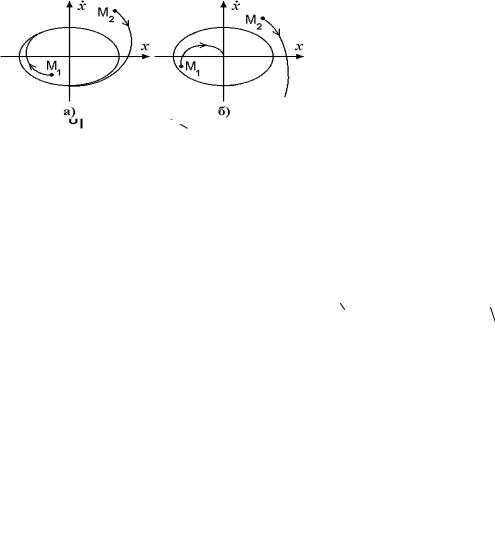
Рисунок 2 - Фазовые |
|
|
|
|
|
пользуют |
|
частный случай ф з вого пр стра |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
назы |
|
инамую |
|
|
фазовую |
|
плоскость. |
|
|
Она |
|
пр |
дставлена |
на |
||||||||||||||||||||||||||||||||||||||||||||||||||
величинапортреты |
, а |
|
качествеСАУ |
системыди |
Чащек 2, |
льзу |
|
|
я ее |
|
|
|
|
|
|
|
|
ная |
& |
|
|
|
|
|
|
|
|
|
|
регулиру мая |
|||||||||||||||||||||||||||||||||||||||
пространст |
, |
|
|
говорят, что |
она у |
|
|
|
|
|
|
|
|
(нкачествева) |
|
|
абсцисс“м началам”. Если нелинейн |
|
|
САУ |
|||||||||||||||||||||||||||||||||||||||||||||||||
устойчива (нелинейной |
|
|
|
вдаликоторыхначала координат, |
|
госи |
|
рят, |
что |
|
такаякоординатемаустойчивы |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(неустойчива)устойчива)“большом”. Обастойчиваэт сп стоянияустойчива)производные- “б льшое”, |
|
выступаеттие“мало ” - |
разделяет |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ринц |
ииальным шибкам. |
|
|
|
|
|
|
|
|
|
|
|
|
всего |
|
|
для |
|
|
|
|
|
|
|
|
дования |
нел |
|
|
|
|
|
|
ых |
|
сис ем |
|||||||||||||||||||||||||||||||||
|
Если |
|
|
|
|
|
|
ная |
|
САУ |
ус |
|
|
|
|
|
|
|
где(н |
|
|
|
|
|
|
|
|
|
|
лизи |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ф зового |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
велич |
|
|
|
|
0 |
|
ее |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-го порядка, где |
|
- |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Следовательно, |
|
|
|
|
|
|
x c |
|
|
|
|
|
c c o |
|
s t , c o n s t . |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
3)4 |
||||||||||||||||||||||||
|
x& a c o s t |
|
|
t |
|
|
|
1 |
|
t |
|
2 |
x |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
x 2 . |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
a |
|
|
|
s in |
t a |
|
|
|
|
|
|
& |
6 |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x& |
Наc e |
фаз |
|
e |
|
|
|
плоскости, x& |
|
ц |
x |
льнойх дящ |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
ч ло |
|
ко |
|
|
б |
|
|
.уравПри |
|
|
|
|
|
тр |
|
|
|
|
|
ли инеез |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
ре |
метра |
|
|
|
|
|
|
|
цесс |
|
|
(3) |
|
|
|
затуха |
|
|
|
|
|
|
|
|
|
временем. |
|||||||||||||||||||||
|
|
|
|
|
|
|
Следов |
ельно, |
|
|
|
|
|
|
ка на |
|
|
|
|
|
|
|
|
|
выражениправлее |
|
|
|
начералу |
||||||||||||||||||||||||||
Р суно 3 - Фазовы |
|
|
|
|
|
к |
|
|
|
|
комплексной плоскости (см. рису |
|
|
|
3). Пр |
||||||||||||||||||||||||||||||||||||||||
|
. На |
|
|
поло |
тельной |
|
величине |
|
прямой, |
|
& |
|
|
ухо |
|
|
ияат |
||||||||||||||||||||||||||||||||||||||
комплек ной |
плос |
ис.3бескп динатедстнечность,вленырдинатоответствутрелка направлющие |
траеотктначаларии ко |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
стемы (3). При э ом |
& |
|
. |
иженставляетхарактерис ическо |
|
точки |
|
|
фазов |
|
|
|
лос |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
Найдём |
|
рь траекторию0 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
если процесс иметеп траеф |
му синусоиды |
|
|
|
|
|
|
|
|
|
соо ноше |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
ри этом длякостикторииости п |
оцесса |
|
|
|
|
|
|
|
|
|
|
|
|
|
х |
преобразований (с |
|
чётом |
|||||||||||||||||||||||||||||||||||||
После возведения в |
квадрат выраже |
ий (5),(6) |
|
|
неслож |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
тождества |
2 |
|
|
2 |
|
|
) можсправедлипо |
во |
|
ь выражеение |
|
|
|
эллипса |
|
|
|
|
|
|
|
|
|
(5)7 |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
2 |
|
|
|
1 . |
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Это |
|
уравн |
|
|
|
|
|
|
|
|
полу сями |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
будет |
|
|
|
|
. |
|
Как |
|
|
следстви |
кости,пр |
||||||||||||||||||||||||
|
|
б) неустойчивый |
|
|
|
|
|
|
|
|
|
ос |
|
|
сти |
|
|
|
|
|
наблюд |
|
|
ть я |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Циклы |
|
|
могут |
|
|
бы ь |
|
|
|
|
у |
тойчивыедвижение |
||||||||||||||||||||||||||||
стремится удалиться от цикла (7), то его называюнеустт ойустойчивыечивым. |
Еслиназываютэт точка |
стремится |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x& 2 |
|
редс авлен |
|
|
|
|
инусоиды |
|
|
|
|
a |
|
на |
фаз |
вой |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5) |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
цикл . |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
эллипсу (7). Его же часто |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
характ р |
|
|
|
|
. Е |
ли |
харак |
еристическая |
|
точка |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
еской |
|
|
|
|
чки |
|
|
|
|
M |
x& , x |
|
по |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
управления. |
|
y( t ) ( bm |
pn m |
bm 1 pn m |
... b1 |
p1n |
b0 |
pn |
)z( t ), |
|
|
|
|
|||||||||||||||||||
где |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
Пусть дифференциальное уравнение порядка n в операторной форме, |
|
|
|
системе, |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
m |
|
n m |
|
|
m 1 |
n m |
|
|
1 |
|
n |
|
0 |
|
|
n |
|
|
|
|
|||||
виде: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
пр |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
описывающееенедставл0) |
|||||||
|
px(t),= d/dty( )––символвход выход системы; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
ai , bj– |
m]; m n. |
дифференцирования;полиномов, общем случае функции времени; i = [1 – n]; j = [1 – |
||||||||||||||||||||||||||||||
|
|
|
равуюкоэффициентыа ть ражения (20) умнож м |
|
|
|
на pn |
(pn / pn) |
|
получим: |
|
|
|
|||||||||||||||||||
z t ) |
|
|
|
pn x( t ) |
|
|
|
1 |
, |
(22) ил |
1 |
z t |
x t |
(a |
1 |
... a |
1 |
1 |
a |
1 |
)z(t |
|
(21)3 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
(20) |
ка ической форме. |
|
а им нно - (21поделим) (23) – легко ожетисходногобыть |
лучена |
|
|||||||||||||||||||||||||||
|
|
Используя эти |
|
|
|
|
|
|
||||||||||||||||||||||||
эквивПолученныеале т ая структурнаязависимости,хема, моделирующая данную сивлсениемте у, которая |
представлена |
|||||||||||||||||||||||||||||||
|
|
|
pn a |
|
pn 1 ... a |
|
p a |
|
|
|
|
|
|
|
|
|
p |
|
|
|
p |
|
|
p |
|
|
цессы |
|||||
на рисунке 5. |
n 1 |
|
|
|
1 |
ти (21)o |
- (23) являются предста |
|
|
|
|
|
|
|
|
|
урав |
ения |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
1 |
|
n 1 0 |
n |
|
|
|
|
||
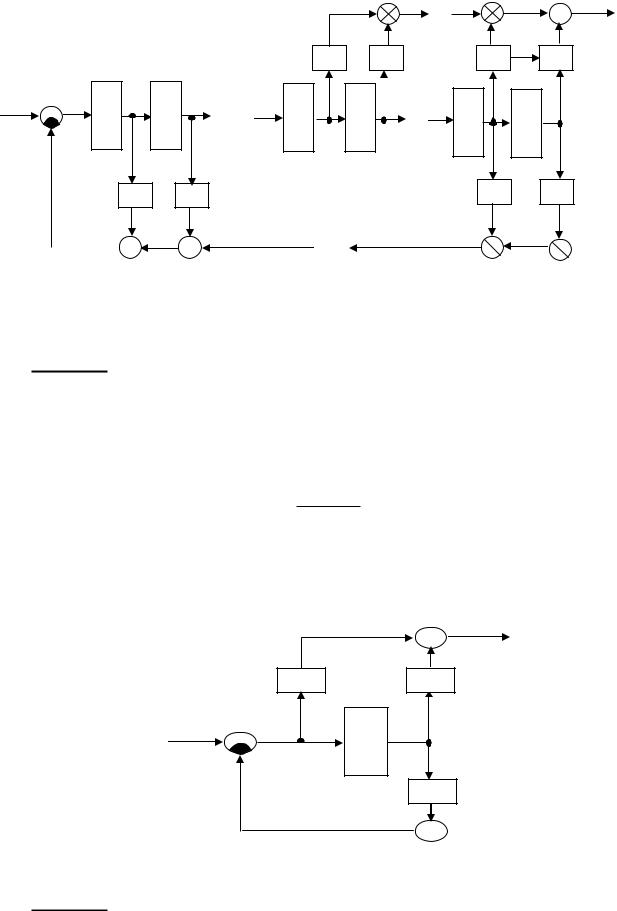
|
|
|
n-1к 5 – Эn-2 |
|
|
структур |
|
|
|
схе а с стемы, соответствующая |
|
|||||||||||||||||
диффИнтеимренциальегро 1.- |
|
|
|
|
дифференциальному уравнм |
|
ию (20) |
|
|
|
следующим |
|||||||||||||||||
примерыдифферых уравнененквивалентниспци льзующее. ниядиописанамичесногокое етодазве предстаописываетсявления |
||||||||||||||||||||||||||||
операторным уравРисуноением (перв го порядка): |
|
|
|
|
p |
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
ППриведем |
|
|
|
|
|
y ( t ) |
|
T |
|
1 |
|
|
( t ). |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
||||||||
к стандартн й форме (20) |
|
|
2p |
0 |
x ( t |
), |
|
|
|
|
|
(254) |
||||||||||||||||
|
T |
|
|
1 |
|
|
y ( t 1) |
|
|
1p |
|
|
a |
0 |
|
|
|
|
|
|||||||||
схгдемыСоответствудля общегоющслучаяая структурн(см. рисуноая схема,к 5 имреализующаяеет вид: |
данное уравнение и получаемая из |
|||||||||||||||||||||||||||
b 1 |
|
1 |
, b 0 |
T |
|
, |
a 0 |
T . |
b1 |
|
|
|
|
|
|
1 |
|
|
|
b0 |
|
1 |
|
0 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
a0 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Рисунок 6 – Структурная схема, |
|
|
|
еализующая дифференциальные |
|
|
||||||||||||||||||||||
Пример 2. |
|
|
|
|
|
|
|
|
|
|
р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Дано операторное уравнение второго по ядка: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
2 |
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
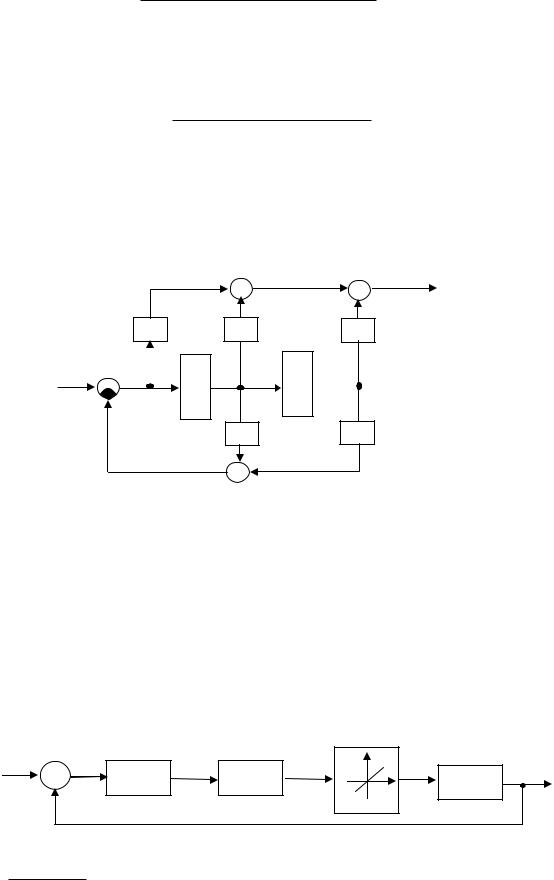
рисуно |
5), имеет вид, представленный |
|
рисунке 7. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
которой представлен |
а рисунке 8. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
построить фазисслвыеде траеов |
кторстационаош бки . |
|
1 |
|
|
|
|
|
|
|
|
o |
|
|
|
|
|
||||||||||||||||||||
|
|
|
1 2 |
|
|
|
|
|
|
1 |
1 |
2 |
2 |
|
2 |
|
|
|
1 |
|
|
|
|
|
|
o |
|
|
|
|
|
|||||||
|
|
|
|
|
|
1 |
|
|
|
|
b2 |
|
2 |
1 |
|
|
|
|
0 |
b |
|
|
|
2 |
1 |
|
|
1 |
|
|
b |
|
2 |
0 |
|
2 |
||
|
4.2.2.1ПримерРисуно. Пост |
7ка зад– |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
процесдифференциав |
льные |
||||||||||||||
|
|
Структурнаяч я нестац онарнaсхема,1 ых |
|
|
нел нейныхa0 |
|||||||||||||||||||||||||||||||||
|
ове |
|
|
иссл |
вание |
|
|
|
|
|
|
|
|
|
ной |
системы,реализующаякнутая |
структурная схема |
|||||||||||||||||||||
оцен |
|
|
пер х дные |
|
|
|
|
|
|
|
|
|
при |
|
задании |
|
|
|
|
вход |
контура |
слежения |
||||||||||||||||
|
скачкообразн |
го, |
|
|
акжпроцеснусосы |
|
дального |
сигналов; |
|
|
|
|
|
|||||||||||||||||||||||||
При этом: |
|
|
|
|
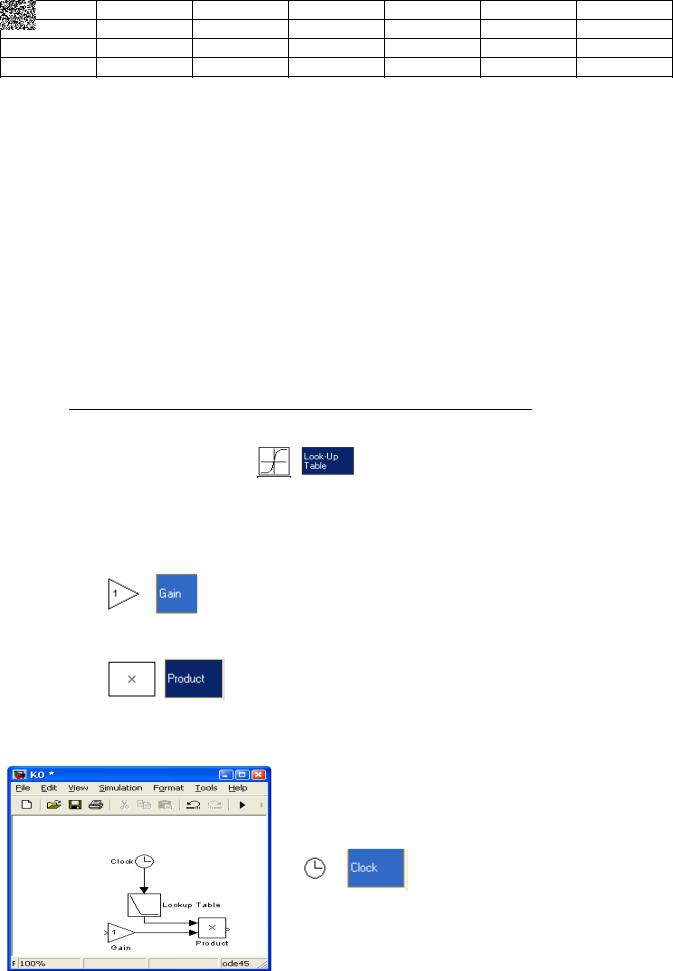
Рисунок 8 – |
Структурная схема |
исследуемой модели |
|
||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
Таблица 1. Исходные данные |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
T ( t )s |
1 |
|
|
K ( t ) |
|
|
|
|
|
|
||
|
x |
|
|
K0(t) |
|
U1 |
W1(s) |
U2 |
U |
W2(s) |
y |
||
|
|
|
|
|
|
3 |
|||||||
W1 |
|
1T s 1 |
|
; W2 |
1s |
|
, T2 = 0.05 c. |
|
|
|
|||
|
|
|
|
|
|
|
|||||||
>> T2=2K10 [1.50..98970..56705..5]0..54 0..5]4] |
|
|
|
|
системы |
|
|
|
|
|
каж ое |
з ено |
||||||||
2). Используя дсистему |
SIMULINK |
|
MatLab |
“наберем” |
||||||||||||||||
-Для-изизУсилразделаэ огоразделфунтельноепон LookдоблооднойзвеноятсяLook-ковUpслпTable-перемеUpMathдующиеременTableнымой);Operations(блоперкикибибдаточн- длотеки:за(мблокиблиц):коэффициентодномернойэлементов, таблицыKопр0 (t)деляющ(в иде |
||||||||||||||||||||
математические-сигналаперации):GAIN,наProductпос; оянныйMatrix- блокоэффGainум–циент)ожеусилизаданиятель |
деления(выполняет(выполняетумноженивычисленвходногоие |
|||||||||||||||||||
произведения |
екущих |
знач |
|
й сигналов) |
|
сумы текущих значе |
|
|
|
|||||||||||
–блокцииSum – |
сумматор; |
(выпол яет |
вычисле |
|
|
|
|
|||||||||||||
исходной ру урн й сх мы. |
|
сигналов):ремени |
рования) |
|
|
|
|
|
|
|
||||||||||
|
|
еличина |
|
|
|
|
на каждом шаге равнаисточникущему |
|||||||||||||
; |
|
|
схем |
|
ри |
|
размещепредставленныйнии блоков |
стррисунктурний) схеме |
||||||||||||
|
|
|
- |
|
|
- |
|
из |
раздела |
Sources |
блоки |
|
|
ков |
||||||
|
|
|
|
Clock |
|
|
- |
источ |
|
к времени |
(формир ет сигнал, |
|||||||||
переменный коэффициент передачи |
|
Схема |
|
|
|
которого. |
|
|
|
на |
|
ке |
9. |
|
||||||
|
использован поворот отдельных блоков относительно |
|||||||||||||||||||
|
|
|
|
|
|
П |
мемоделчанвид,. |
|
Для обеспечения |
добства |
чтения |
|||||||||
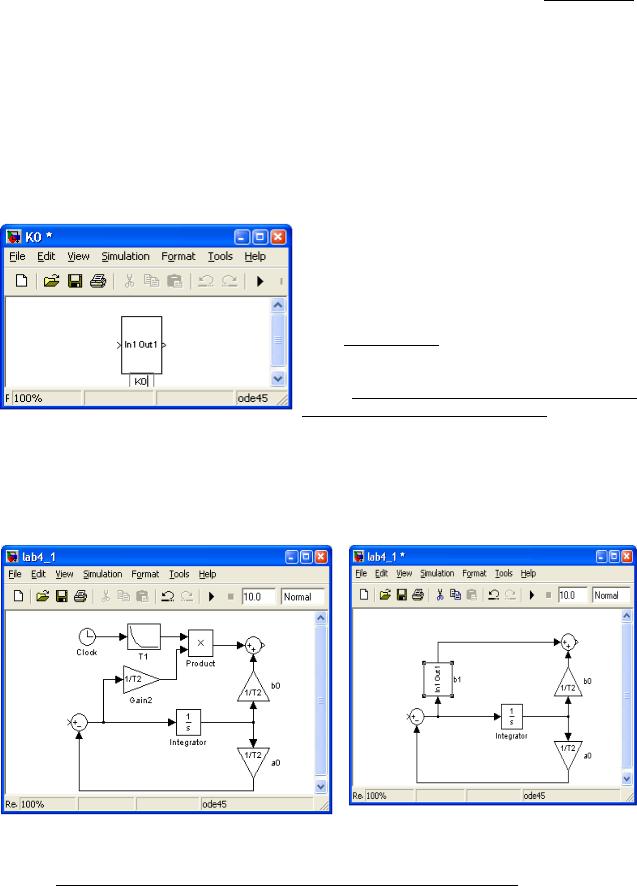
реализующаяможноструктДляблокиобъединитьрмированиярнойудф бствауказанноесхемы,группуодинкоэффицкотораязвено,блоковпрприметентасвоитьбудетнаK0рисункевид,имяа алbпредставле1вос.11,гичнаператорноформирующеменПРавленИнтзулвитьивнныйп денчаедстатгронапвыражумяиенастоя-рисункедифференцирующееоеих.влрисункещелчкамипеременныйнаСнойиетакогоставсхеме10Wвремени.11налевой.предодсистемырисунке(смкоэффициент.тавTобъед1ропки(t)звеносунокм6.Схема,мышможно0ненвидеW1b8)я
РезультЗвеноУсилительноеРисунок“набирается”атирующаяпредставл11 – схСхзветакименмаозвенаспррисункежедставленаременнымWобразо1 12. ,напередаточнымкакрисунзвеноке 13K. (t)коэффициентом. блоками K (t)
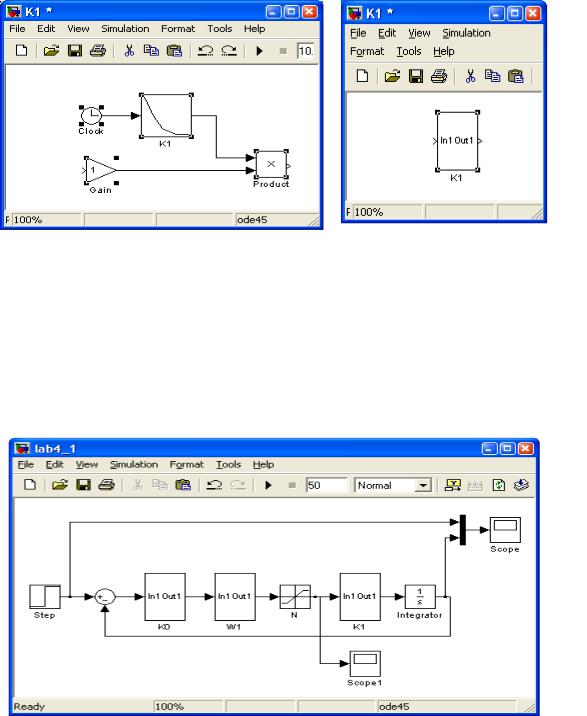
соответствующуюнелинейностьюпредставлено3)ПоИтоговаясле насхемаNрисувание(типакедля“насыщение”15моделирования. переменнымииспользовать), интеграторнашемисходнслучаеке любойм может, а такжевыглядетьсумматоропеременныхтак,получимкакодельэто.
графиков:выходеplot. Д-4)либоблок.нужногояИсисследосцграфзап оллсиблопванияграфасткасистемыабочуюоительпрScope;следующимцессовXY.областьGraf;можноMatLabпостроениемTo Workspaseграфиков исследуемыхизиспользованиемспособов едставленияоператорна
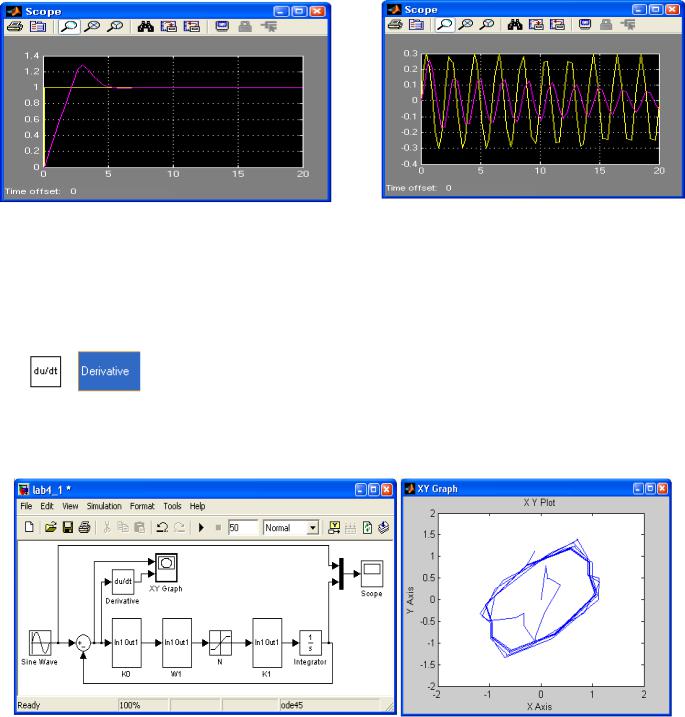
dΔ/dt=f(снабженнаялтегичениемконалаНаКакДляПолучимполучить,Δ)Aвреслрисун.sin(ω*t)этого,блодуетени,комфакакизпричтоеслиовую18группывычисленияассмотренияказаноA=1вызваноприведенатраевоспользблоω=1/выше,ктпепроизводнойриюсхемаContinuousад/cватьсясунканностьюобходимоошибки. (аналогичная17,бло. А.амплитудакомэффицпририсуетьвычислепомимозаданиииентакепредставленнойых19нияпередачидного–ошибкфазоваянапроизводнойвхс Kдегналатраектория0,скоростьKсину1 уменьшаетсяворисункевремениоидальногоDerivativedΔ/dtошибки.15),Еес
