Методичка ЛР_МоСисУп

s^2 + 10

+ 100

воитьвести названияпри помощивходампроцедурывыходамset

некоторыепрямой После100-------------------------------------------------------------------Tranобратнееs^4ferсимвольные25того,+function:s^2й цепика+ ^3процсистемаописания250дурой0s^2сформирfeedback:. 8000В частностиsва 5 00можно.

системы,>> такжеsget(sysnum:,'Notes','УгдатьInputName','Моменткрат250 25кийовое2комментарий.5e+движение03]}сил', 'OutputName','рпеды')самой присУголистемерыскания').

den:

.05e+003 1.06e+004 8e+003

5e+003]}

Ts:1050

y:{[0

ys=feedback(W01,U)el y:

анализа

InputName:Not s: {'Угловое

дв жение торп ды'}

сущ

Пакет CONTROL

пред ставляет пакет процедур для

прежде всего, для

опредположния отклика системы

внешние

здействия как

временнойСАУ,

ioDel

{[10y:

Variab

's'

OutputGroup:[1x1struct]

з системы

{'Мом

сил'}

я'}

Общ

ыска

анал

я

1.3.1.1. Пр

за во временн й

im ulse

Нахождение

отклика на импульс ое входное воздействествления.

UserData:

[]

некоторых

Для Аналобластяхмеры вр менных откликов областистемы на внешние

step Нахождение

реакции

системы на единаичный скачок входноговоздействия.

так в частотной

.

видов предусмотрены функци :

казы ающиеmargin. .1.3. расп л жениедуры,иагр ммулюсБ де

казансистемыотдельзапасовые характеристикипо амплитуде и и

фазеграфичес.

ole Расчет

люсов

истемы.

СтроитРасч

юсов,вычисляющиенулей эффициента передачи системы.

п люсов zpkdataсистемыzmap .

строение

на

пле

й плоскости карты

расположения нулей ки

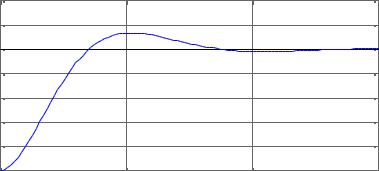
1>>Применяя.3step(sys).2. Примерыпроцедуруана изаstepво временсозданулейксноййобластив п. 2.2 модели,

можно получить график

Step Response

7

From: Момент сил To: Угол рыскания

0.6

5

4

3

2

1

0

0

5

10

15

Аналогич о,

дуры impulse

>> impulse(sys)

приведет к появлениюиспользованиеграфическомпроцкне графика, приведенного ниже:

-0.05

0 0 1],20)

5

10

15

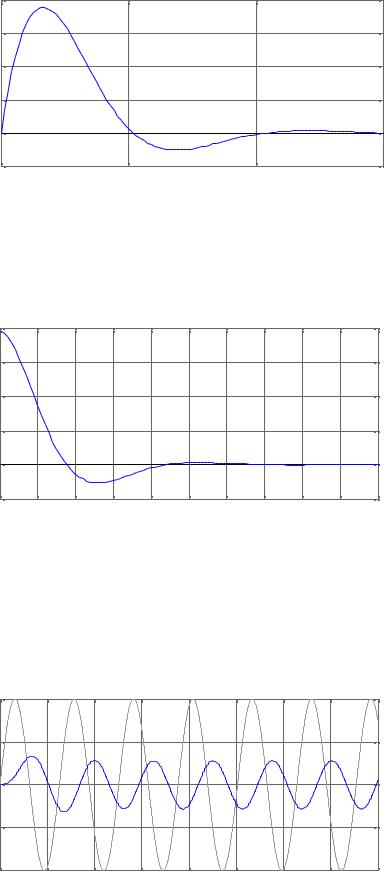
>> initial(sssys,[0sssys= 0(sys)

Получим

4

Response to Initial Conditions

0.3

-

2

01

0

2

4

6

8

10

12

14

16

18

20

векторзначенийuДлязначенийвремени,применениявходнойкоторыхпроцевеличиныбу рыт заданыв казаннеобходимоыеачениямоментывходногопредварвременивоздействия,т льно задатьзатемвекторзадатьt

>> t=0:0.01:40; u=sin(t); lsim(sssys,u,t);grid

Результат представлен на следующей фигуре:

1

Linear Simulation Results

-

0.05

0

5

10

15

20

25

30

35

40

-1

42

Magnitude(dB)

6

00

Phase(deg)

-

-9

-2

10-1

100

101

102

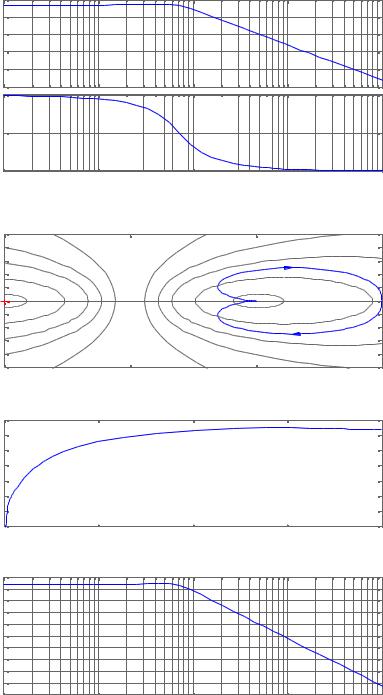
yquist(sys)

Frequency (rad/sec)

180.6

Nyquist Diagram

4

2 dB

From: Момент сил To: Угол рысканèÿ

-4

0 dB

-2 dB

-10 dB

6 dB

-6 dB

4

1

-20 dB

ImaginaryAxis

2

20 dB

- 10

8

-1

-0.5

Real Axis

0

0.5

nichols(sys)-1

Nichols Chart

10

From: Момент сил To: Угол рыскания

-2

3

LoopGain(dB)Open-

4

5

6

-135

-90

-45

0

-180

sigma(sys)

Open-Loop Ph se (deg)

Singular Values

1

-2

3

4

5

SingularValues(dB)

6

70

8

9

-100

10-1

100

101

102

10-2

>> margin(sys);grid

Frequency (rad/sec)

Magnitude(dB)

2

400

Phase(deg)

9

35

-180

2

10

1

100

101

102

10

anspole(sys)

Frequency (rad/sec)

"Угол рыскания":

(s^2sysz=zpk(+ .25 (s^2fromys)+ +.5128)10sinput+"Момент100)(s^2 + 9.сил"731sto+ output97.5)

z [z,p,k]=zpkdata(sysz,'v')

Zero/pole/gain5 0000

------------------------------------------------04.38478653 7693s+0808..5924i040603i

k =

0.2500

>> pzmap(sys); grid

Результат представлен на рисунке ниже

0.4

Pole-Zero Map

0.14

0.09

0.04

8

8

56

0.28

0.2

ImaginaryAxis

6

-246

0.8

2

-108

4

56

0.4

0.28

0.2

0.14

0.09

0.04

6

-4.5

-4

-3.5

8

0

-5

-3 -2.5

-2

-1.5

-1

-0.5

Задание

самостоят ль

Real Axis

ую работу

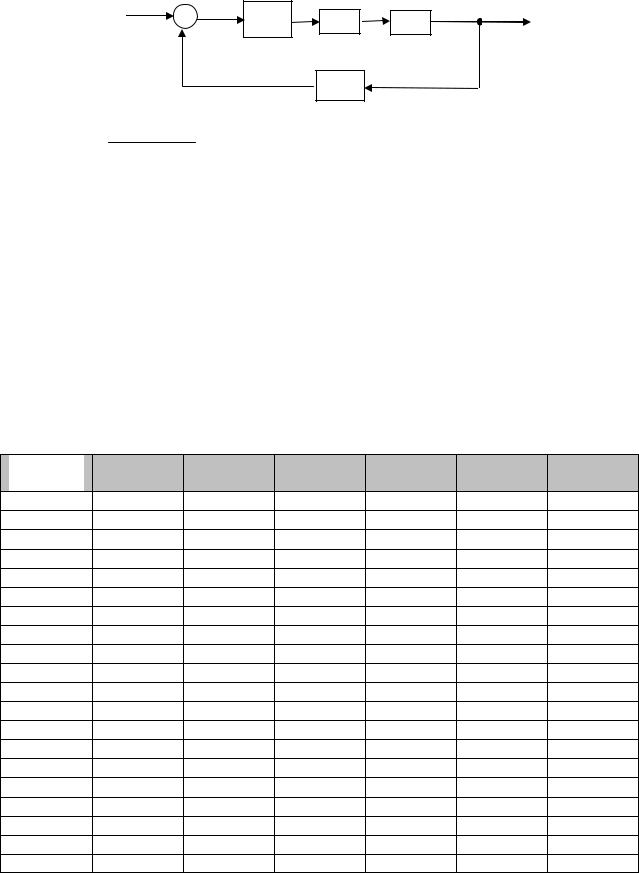
1.4.1. Структурная схема

Создать модель системы слмоделижения, представленной на рисунке:

-- 1

дел

2

реакциюлю

систенули2к

34на г .

; 3

в

пр

1

П едст ить

рафи .

уст йч во ть системы показатели

Копрценитьрием

при

ис ледованики до жны

ва

к чества.В случ

неудсоответствующительног к

здействия;при х дных параметрах (см.

т бл цу вариантов)

брвлетвоь

ебуемые пара

служитьры системыкорр ктирующего фильтра W1(s) T1, T2,

Kпр.

1.4.3. Исходнвременнпараметрыые

модел

Исходные параметры заданнойсистемырмоничесы для каждогокие варианта заданы втаблице:

варианта№

T1, c

T2, c

T3, c

T4, c

5

Kпр

Kос

6543

4032

4320

9

1

11

8

30

10.0

95

0.0045

9

1.0

20

0.700

0.065

0.050

8.0

7

2

8

8

1

6

100

6

50

7

2

4

90

30

3

5

5

5

40

25

7

6

6

80

4

5

19

4

полезной

другой физической ве ичине, содержащейся

измере ном

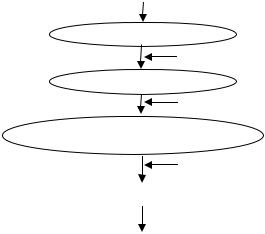
целях полученияОбщая информациисхема образования змеряемогочине, которая до жна бытьпроцессаизмерена,его преобразовапредставленаия

р сунке.

Измеряемая

Полезный сигнала

П рв чныйИзме итель

Шумизмерителя

Измеренная

тный

еобразователь

Дис

Массив измеренийОбработанная инф

мация

на

ке служит для

ор

ния входного дискретного во времени

сигнала выходн й

нимизаци

искажений,

шумами.

аналоговых

Пакет MatLab Signal Processing Toolboxпреобраз зволяет:

цифровых

рассчитывать конкретныевеличинасловые хар

ктеристики

льтров

по

АФЧХ;

льности. Форм

ие

ных процессов

нале.

О

средства

требуемымОбщиеосновы линейной фильтрациповых

прим ре линейного стационарного

Фильтрация –

это

реобразов ние заданного сиг аласлучайпомощью линейного фильтра.

фильтраРассмотрвт рого порядка,

передаточнфильтраця функцияктированныхкот ого имеет вид:

ф

(э страп лят

+ АЦП)

еменных сиг алов;

ми овать п след ват

- обра атыватьисунх при помощи спрое

Шум дискретизации

фи ьтров.

2.2.1.

льтраци

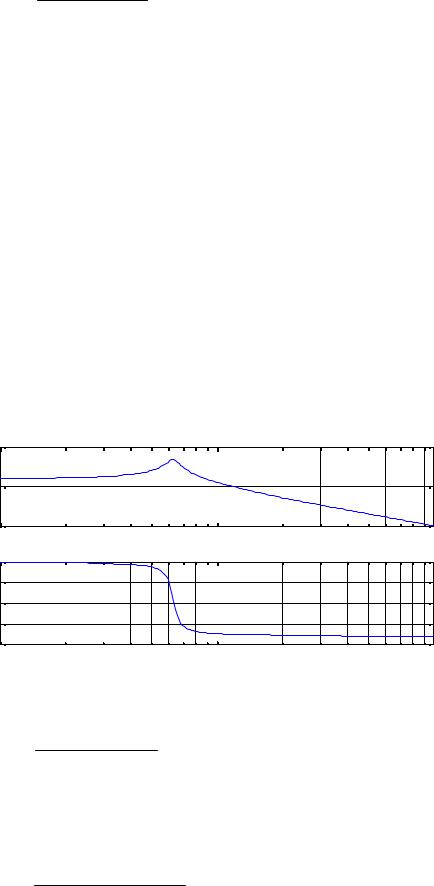
частотная характ

еристика

.

Пример.

числителя

знаменателя и выведем графики

ВычислиA=1; ξ=0м.05;значения2π /коэффициентовω =1.

АЧХ и ФЧХ:

.05;

T0=1;dz=0a1(A=om0=2*)= pi/T(2)0;a=12*dz*om0;a1(3)=om0^2;b1(1)=A;

>> freqs(b1,a1)

10

2

101

102

-4

-

100

-0050

Frequency (rad/s)

2

0

101

102

Дискр

ная

передаточная

ф

Frequency (rad/s)

непрерыв

му

фильтру (1)

соотв тствующая

(которая

мож

т

быть получена путем Z - пр образования

разностного

уравнения -

дискретного аналога дифференци

льного

урав

ения),

меет вид:

( z )

2

кция,

(2)

0

1

ATs

a

2

1

2 z 2

где a

(ω0

(ω0

0

-

Ts) ;

(1+ξ

10 Ts));

1

a =1+2.

2

В

общем случае дискретная передаточная функция имеет вид:

y

b

0

b

z 1

... b

m

z m

G( z )

(ωTs)+z

1

n

(3)

x

a0

a1 z 1

. an

A1

75;

(2*pi*t/T1);

Yp

A1*si

'P-signal')

y

T1=1;

P-signal

t,Yp),grid;

8

6

Yp

- 4

6

8

6

8

10

12

14

16

18

20

t, c

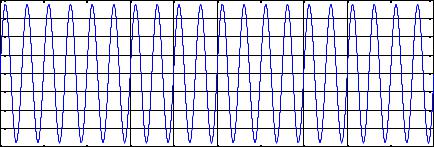
A2измерения=10;

к

полезному-Пустьбсигналуо ыйеевслевысокгауссовдобавилисьчастотнаяиекийпрохшумшумы:ожденсизмеритнусоя чдалярезс периодомспреинтенсивностьюбразователь=0.2 cAшиивамплитудой=5результате.

В

результате создается такой измеренный сигнал x(t):

T2=0.2;A2=10; eps=pi/4;

ndn(1,length(t));

Ash=5;

grid

p ot

title

'inpu

xl=A1*sin(2*pi*t/T1)+A2*sin(2*pi*t/T2+eps)+Ash*rat,x), c'

>> ylabel('x(t)')