Методичка ЛР_МоСисУп

x(t)

-30

4

6

8

t, c

12

14

16

18

20

фи ьтр, Тч.к.при

ериодомощи егорезонаб

ноготвеигналаныхфи ьтзаранеевида (2известн.TфПрибылэтомворавеннеобхперилениемо

у ездатьк лебаниможтакой

лезного

Tф= T1 .

восстановле но

Чтобы

после пр х жден я через так лебанийфильтр амплитуд

а

выполнитьс впадала игнавеличинуплитуд

2ξωлезного(посколькула,

ужно входнойамплитудасигнал фильтраыходномнгогожсигналть

уменьшаетстояннуюя именно во

стольк

раз по сравне июрезонансеамплитудой входногосигнала).

a(3om0T1=1;2 A*Ts*Ts*(2*dz*om0^2-;+2*dz*oms+oms^2*(1+dz*oms)pi/TfфильтA=1;o.05;опs=om0*Ts;сансигнаый выше:

Проп стим сформированный процесс через него:

0002:end)),grid

ptitle(1)=otfilter'procesOut(Tf=1,dz=00002:end),t(10002:end),Yp(1.05 ');

x

t, c'

>> ylabel('Y(t(b,a,x);')

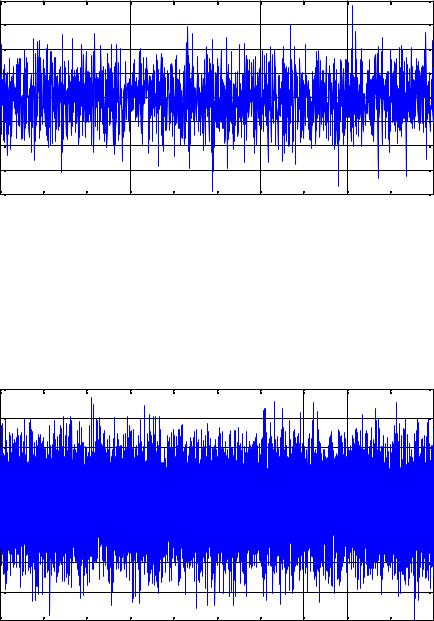
СформируемВ рез льтате получим процесс, приведенный на рисунке.

8

procesOut(Tf=1,dz=0.05)

Y(t)

.6

4

-t(10002:end),y(

6

8

-1

0

2

4

6

8

10

12

14

16

18

20

t, c

Из рисунка можно заметить два недостатка:

1

procedure FILTFILT (Tf=1,dz=0.05)

8

0.6

Y(t)

-

024

6

8

-

0

2

4

6

8

10

12

14

16

18

20

t, c

распредел2-Сф.2а.2сначала.затемФироватьб лым“пр сформировшпуститьмослучайных, процерпроцессйныйкотзаданроеойпроцесс,д корна ичляцикоеявлянойзвеноийсяфункцией(форми ующальножно,

фильт

”.

х д

та

го зве

п

распред ленный

процесс

если:

Б

лый

функцией,

егок тор

опред ляе ся т

формирующего фильтнор .

гаусс

ый шум

MatLab

образу

тся п ипомощи процедуры randn.

Для

э

го

д статоч

задатьлучаетсяди крет време

и Ts, образовать с этим шагом массив

(вектор) t

момен мированиевремеслучайныйвид

м диапаз не,

затем сформироватьслучайныйпо казанной

процедурекорреляционнто

-столбец длиной,нужнрав ой длиненормальновект ра t.

Например

p=0:Ts:20;1ot .0

title 'Gaus T=0.01c)');

xl

t,x1),grid;c');

>> ylabel('randn(1,length(t)X1 t)')

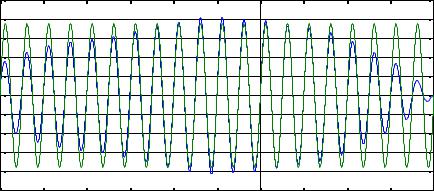
Соответствующий процесс имеет вид:

X1(t)

-30

4

6

8

10

12

14

16

18

20

=0:Ts: 0;

t, c

pxltitle2=randn(1,length(t))ot t,x'Gaust,),grid;c');Ts=0.001 c');;

Gaus Ts=0.001 c

>> ylabel('X2(t)')

4

3

0

3

4

0

4

6

8

10

12

14

16

18

20

Создадим

д

кретный

формирующ йt, cфиль р

второго

порядка

с

собственных к

лебан

ω0

2π рад\с =1 Гц

относительным

коэффициентом колебаничастотой

затухания ξ=0. 5 по

выражениям

(2)

коэффициентов:

om0

2 pi;

=0.05;A=1;oms=om0*Ts;

2

-2

s+oms^2;

1+dz*oms;

a(y1=filter3 ;

b(1)=A+2*dz*o*oms^2;

ропустим

бразованный процесс x1 через созданный формирующий фильтр:

>>

(b,a,x1);

Построим соответствующий график:

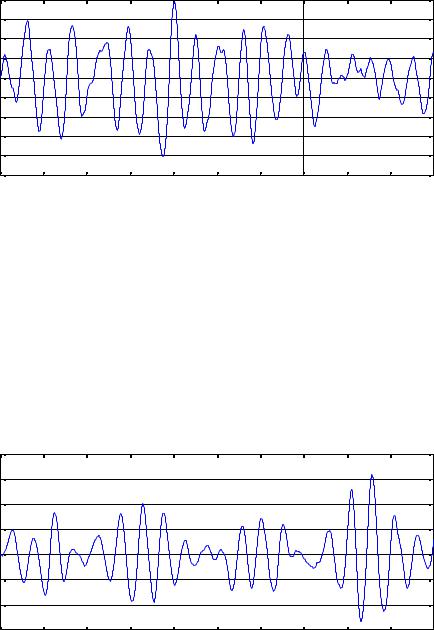
Y1(t)

-

.

01

om0

43

5

0

4

6

8

10

12

14

16

18

20

pi;

.05;A=1;oms=om0*Ts; t, c

a(3(1)=A1- +2*2*dz*oms^2;1+dz*oms);s+om ^2;

2=fi ter b,a,x2);t=0:Ts:20;

pxtitleot

t,y2),grid;'procedurec');

(T0=1;dz=0.05;Ts=0.001)');

>> ylabel('Y1(t)')

procedure (T0=1;dz=0.05;Ts=0.001)

8

Y1(t)

0.06

24

-

0

6

0

2

4

6

8

10

12

14

16

18

20

Как видим,

t, c

дейс вительно образуется слу айный

формирующ го фильт

колеба ельный пр цесс с преобладающей

1 Гц.

Спек ральный

атистический

ализ

2.3.1.

вные

с

льного

нали а

–

выявлен

ес

пектра этих

зад ча

армонич

ча

то

выходе. .

пределе

ие стотойчас

ких

сигнала

выявление

спектра),

мпл

уд

этих

).

составляющихксоставляющ

(амплитудного

сигналов,спект )

их начальных фаз

(фаз

сигналов

В осн ве спе

ан

лиза

лежит тоеворияпектрФурьгармоничеса возможности разложен я

любого Основнаяпери дическтральногопонятияцесса

на

счетную

сумму

отдельных

гармоническогоих

составляющих.

j

m 1 )( k 1 ) / n

j m 1 )( k ) / n

m

функции,Входной

суммой

ух синусоидвиде вектора,с

элементыи 5которогои 12 Гцравны. Найтизначениям

k

изображения:являюэтогощсигналаейся представимвывести

графики входногчастотампроцесса и модуля его Фурье-

=0:0t,x)'input'). grid;

input

xl

.

, c'

X(t)

0

001:2;

-

-2

0

0.2

0.4

0.6

0.8

1

1.2

1.4

1.6

1.8

2

fft(x);

t, c

=sin(2*pi*5*t)+cos(2*pi*12*t);abs(y);

p ot

a);g

d;

title

'fouri

x

number');

>> ylabel('absF(X(t))')

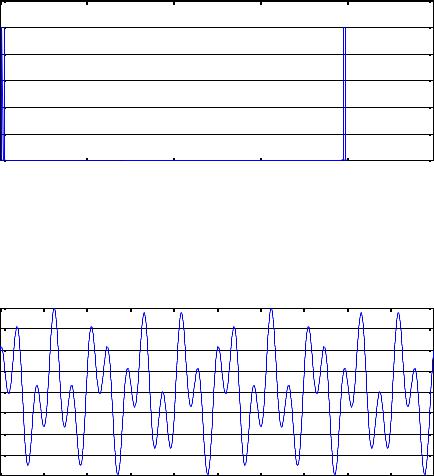
8

absF(X(t))

600

4

x

500

1000

number

1500

2000

2500

20 0

t, c');

>> ylabel('Z(t))')

inverse

Z(t))

1.2

-1

2

0.

0.4

0.6

.8

t, c

1.2

1.4

1.6

1.8

2

совпада ИзКас

аж

. из(4) можноследнего

т

исть:

ден

ый проц сс

точности

ка,

в

x(m);

m со

ветствует

ме ту в емени tспроизвm , к

ый измерен вход

ойден ый

эле

т y(k)нодискрследуетер k –

огэ

и

кс зн ч

Фу ье;

fk, к

му

д

сходнымпе

индексов

к

вре

енной

рый

отной

бластям,

обходимо знать

пр межут

шага

h

кр та

врем

,

через

гн

x(t)сигнал,

T

в еменний, на протяж

ания

Df

1/T,

измерен; тогдасоответствувходной

част те

из

браже ии Фу

ье

аж

значениедиапазо

изменения частоты

– выраженинием

F=1/h.

Таквынашем

импреобразDf=0.5, F= 1000.

в

-

Фу ье - из праж

тся функцией fft толь для положительных част

ы; более

0

F, что

еуд бно для

по

роеония

Фурье – изображе ия от

удобнымеделяетсяявляние

пе

которогове ору Фурьеизмере– кображения, определен

ому в

диап пазонечастот

[-F/2 -

F/2].

Сформируем

для

данногопределяимеходра частотыма сив частотграфивыведем графикретси аргументом

частотой

f=0:0.

'

>> plot(f,a)5:1000;grid

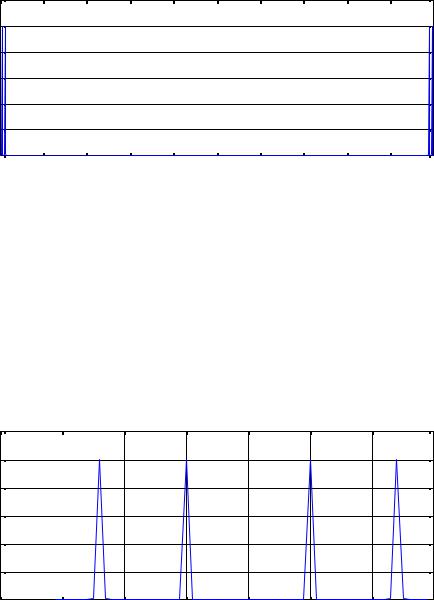
18

abs(F(X))

6

4

20

200

300

400

500

600

700

800

900

1000

преобраз

ть

friquency, Hz

я с пом щью процеду ы fftshift.

вект р y Фурье –

Она предназначена для

вания нового изображенz из заданного у путем перестановки

второй половиныполученныйвектораформирв пе вую половину

ктора z

f1=-500:0.5:500;

fft

(v);hift(y);

F/N

2

abs(F(X))/N')

1000

8

abs(F(X))/N

6

4

-15

-

-5

0

5

10

15

20-20

friquency, Hz

две гармоники- 5

12 Гц.

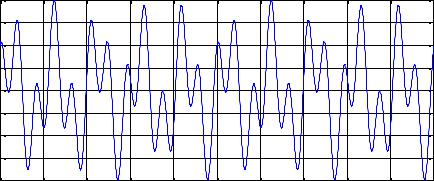
Из графика видно, что в спектре входного сигнала ес

Неудобным являе ся т что по графику невозможно определить амплитуду этих

гармоник. Чтобыp ot f1(970:1030),a(970:1030));grid;сделать это, необходимо весь

вектор y

разделить на число его элементов N:

xa=abs(v)/N;title 'F/N');friquency, Hz');

>> N=length(y);label('abs(F(X))/N')

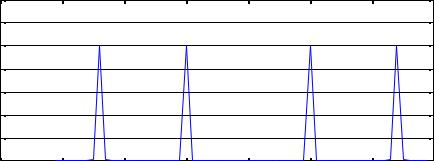
0

0

0)

-

сигн л;

1

= A1sin[(2π/T1) t] – змеряемгулярный шум

ряд

теля;

Aф, ξф

при

ш

– шумбризм дисрений,

интенфильтрвностью(полезный)вт рогоAш.

вида (2) парам

где 2

2

0.45

2

3

-15

-10

-5

0

5

10

15

-0120

ести цифровую обработку

friquency, Hz

ов:

стемы.

0

1

его

ш

й

вен

риоду

колебаний полез

ого

условии, чт

период

собственных колебан

сигнала,

выделяемый

случгналслучайногомакизмеряемыйпроцельнпроцессавоспропреобразовиз белоговодитбелогошума,представляетшумазныйиспользуясигнал.

форм рующий

фильтр втор го

к лебанрядкакретныйвида (2)

ξфф.

собственных колебаний fфф трамиотнос тельным

Представить3

все

ответстпроцеующиечастотойкак суммаграфикигармоник.

ида:

коэффициентомСфор Формированиевать проц сс на

ыхо

стемы

x4(t)=A

sin[(2π*f4*t];

де системы.

Выполнить

спектральйный лизсигналана

трех

Исходные парам

рызатуханияисследований дляследующегокажд варианта заданы в таблице.

2.4.5.

Отчетность по лабораторной работе

Результаты

исследоваданныеий

для

отчета

оформитьвыхтекстовом процессоре Word.

На

ыходе

системы

x(t)

со ой сумму

x(t) = x (t) +

x3(t) + x4(t),

4

Исходные

))/N (X (F s ab

3

3

3

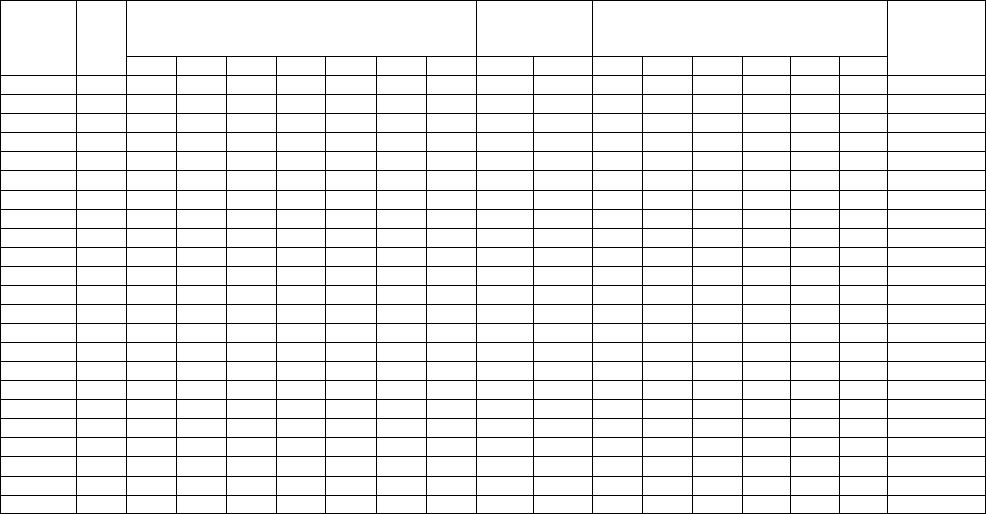
1910876543

1

0.8759

103.5

150

5

5432

13

5

4526

2

2

876

2

12

12

2

329875

628

1234

22

0.005

1

2

7.5

1

5

1

0.05

7

0.05

1

1

4

2

0.5

3

поведения элементов

целом во вр ме .

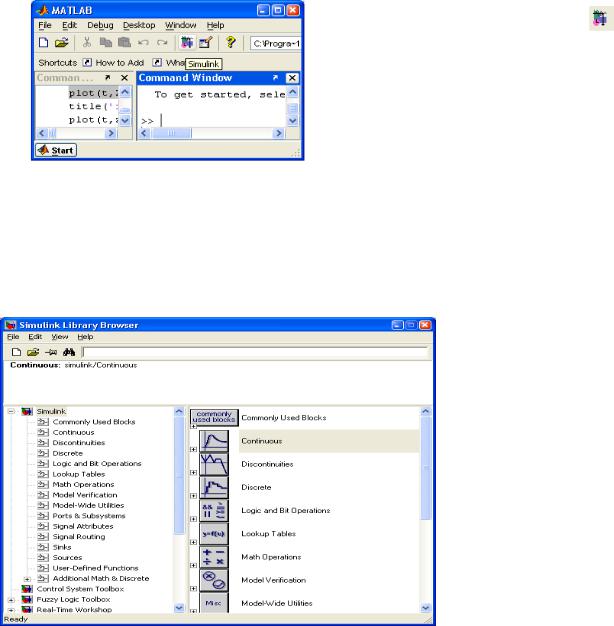
3.1.1. Запуск подси/илисистемыSIMULINK

Осуществляется после

предварительного запуска системы MatLab одним из трех

спо об в:

(рисунобратьнелиоткрытьвыполнSIMULINK1)жансстро;файлиемукетькнтовделмандногоки системыSIMULINKOPEN(mdl- TER;кнаенюMatLab–FILEприна

спослюбкоторыхБибгоБиблиотеовусможно,ройствакрываетсяка разбитакасоеди.Рисубл нокаяяноквряд1модулиобозревателяSIMULINKразделов,линиямиосновныебиблиоте– этозапуснаборкциональнизкикенихПрилоковужевизуальныхперечисленыготовой(рприменесунвязи,опциюкобъектов,отлаженннажа2)составлятьиже. (попервыхфайл)алфавиту):приб оделипомощ-схемудвух.

Continuous – блоки аналоговых элемефунтов;

ontinuitiне й s –

элем

диснтов;кр

элем

нтов,ных

операции;

Discrete -

математичесопределяющик е

Math

–

Opera

tions

блоки

ing

nal

–

&

Si

Rout-