Добавил:

VadoZ хачю сдать сессию Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский технический университет связи и информатики

Предмет:

Высшая математика

Файл:

линейная алгебра и агалитич геом

.pdf

Скачиваний:

Добавлен:

01.06.2024

Размер:

1.34 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 97 8 9 > Следующая >>>

во	M2×2 . Матрицы	1		0	,	0		1	,	0		0	,	0		0	линейно независимы.
			0	0			0	0			1	0			0	1

(D) Рассмотрим линейное пространство многочленов P2 . Очевидно, что мно-

гочлены 1, t, t2 линейно независимы. (E) Рассмотрим линейное пространство

n . Очевидно, что n упорядоченных наборов (1,0,...,0), (0,1,...,0), (0,0,...,1)

(в каждом наборе n чисел, в k -м наборе на k -м месте стоит единица, остальные нули) являются линейно независимыми.

Определение. Размерностью линейного пространства V называется максимальное число его линейно независимых векторов. Пусть это число равно n . В этом случае пишут dimV = n . Такие пространства мы будем обозначать Vn .

Определение. Пусть имеется пространство Vn . Тогда любой упорядо-

ченный набор из n	линейно независимых векторов {e	}n	пространства	V
	i	i=1		n
называется базисом	этого пространства, если x Vn	αi такие,		что

x =α1x1 +α2 x2 +... +αn xn .

Во всех примерах (A)–(E) указанные системы линейно независимых элементов являются базисом в своем линейном пространстве.

Координаты вектора линейного пространства Vn в некотором бази-

се. Пусть имеется линейное пространство Vn и в нем фиксированный базис

{e1,e2 ,...,en }. Пусть a Vn , тогда можно записать
a =α1e1 +α2e2 +... +αnen .	(13.1)
Это выражение для вектора единственно.
Следовательно, вектор a однозначно соответствует упорядоченному на-
бору (α1,α2 ,...,αn ) коэффициентов его вырaжения (13.1)	через базис {ei }.

В этом случае говорят, что упорядоченный набор (α1,α2 ,...,αn ) – это коорди-

наты вектора a в базисе {ei }. Формула (13.1) – это разложение вектора a по

базису {ei }. Заметим, что базис мы зафиксировали, в другом базисе координаты вектора a будут другие.

Вернемся к рассмотрению линейного пространства Vn . Возникает следующий вопрос: как меняются координаты вектора при переходе к новому базису? Закон преобразования устанавливается матрицей Te→ f , которая зада-

ется следующим образом. Пусть имеется два базиса {ei }и {fi }в Vn . Тогда

можно записать, что	fk = t1k e1 +t2k e2 +... +tnk en , k =1,...,n , так как любой век-
тор пространства Vn	однозначно записывается через базис {ei }. Запишем по-

следнее соотношение в матричном виде:

									t	t
									11	12
( f		, f		,..., f		)= (e	,e	,...,e	) t21	t22
	1		2		n	1	2	n	.... ....
										tn2
									tn1	tn2

...	t
	1n
...	t2n .	(13.2)
....	....
...
...	tnn

(Подробно о перемножении матриц см. лекцию 2.) Матрица

Te→ f	= (tij ) — это матрица перехода от базиса {ei } к базису {fi }. Матричное
соотношение (13.2) можно записать в виде f = eTe→ f . Заметим, что матрица
Te→ f	является невырожденной, поскольку ее столбцы линейно независимы.

Правило преобразования координат вектора при переходе к новому

базису.
Соотношение					(13.1) можно записать в матричном	виде:
		α1
a = (e ,e ,...,e			α		= e Α, где Α – вектор-столбец (матрица размера n ×1,
a = (e ,e ,...,e		)		2	= e Α, где Α – вектор-столбец (матрица размера n ×1,
1 2	n
			αn
			αn
составленная из координат вектора a ). С другой стороны, a = f Α' ,						где Α'

– столбец координат того же вектора a в новом базисе {fi }. В силу (13.2)

f = eTe→ f , тогда a = eTe→ f Α' , и в то же время		a = e Α.	Из единственности
разложения по базису имеем T	Α' = Α, или	Α' = T	−1 Α. Заметим, что
e→ f		e→ f
	61

обратная матрица Te→ f −1 существует в силу невырожденности матрицы пере-

хода.

	Пример. Рассмотрим пространство V3 с базисом {ei }, и пусть базис{fi }
выражается			через			базис {ei }по формулам	f1 = 5e1 −e2 −2e3 , f1 = 2e1 +3e2 ,
f1 = −2e1 +e2 +e3 .					Матрица перехода от базиса {ei }к базису {fi } имеет вид
	5		2	−2			3		−2	8
T	=	−1	3	1		, обратная матрица T	−1 =	−1	1	−3 .
e→ f						e→ f
		−2	0	1				6	−4
		−2	0	1				6	−4	17

Пусть задан вектор a = (1,4,−1) в базисе (e1,e2 ,e3 ), т.е. a = 4 . Тогда

−1

	3		−2	8	1		−13
a ' =		−1	1	−3		=	6	. Значит, его разложение по базису
					4
		6	−4	17			−27
					−1
( f1,	f2 , f3 ) имеет вид a = −13 f1 +6 f2 −27 f3 .

Лекция 14

Определение. В пространстве Vn задано скалярное произведение, если любой упорядоченной паре векторов a,b Vn поставлено в соответствие действительное число, обозначаемое символом (a,b) и называемое скалярным произведением векторов a и b, причем это соответствие должно удовлетво-

рять т.н. аксиомам скалярного произведения:

1)(a,b) = (b,a) (свойство коммутативности),

2)(a +b,c) = (a,c) +(b,c) (свойство дистрибутивности),

3)(αa,b) =α(a,b), α (свойство однородности),

4) (a,a) ≥ 0 , причем (a,a) = 0 a =θ , где θ – нулевой элемент пространства Vn .

Определение. Если в Vn определено скалярное произведение, то это пространство называется евклидовым пространством. Будем обозначать евклидово пространство символом En .

Пример. Пусть	в	Vn зафиксирован		базис	{ei }. Тогда для любых
n		n
x, y Vn x = ∑αiei ,	y	= ∑βiei .	Определим		скалярное	произведение
i=1		i=1
(x, y) следующим образом:
			n
		(x, y) = ∑αi βi .				(14.1)
			i=1
Проверим, что (14.1) определяет скалярное произведение, т.е. проверим
					n	n
выполнение аксиом 1) – 4). Действительно: 1) (x, y) = ∑αi βi =∑βiαi =( y, x),
					i=1	i=1
n		n				n
2) (x + y, z) = ∑(αi + βi )γi		= ∑(αiγi	+ βiγi ) = (x, z) +( y, z) , где			z = ∑γiei ,
i=1		i=1				i=1
n	n				n	n
3) (αx, y) = ∑ααi βi =α∑αi βi =α(x, y) ,				4)	(x, x) = ∑αiαi = ∑αi2 ≥ 0,
i=1	i=1				i=1	i=1

и равенство имеет место лишь при всех αi = 0 .

Введем понятие нормы (длины) вектора из En . Для любого x En опре-

делим норму по следующей формуле: x = 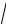(x, x) . При этом в ыполняются следующие свойства нормы:

1) x ≥ 0, причем x = 0 x =θ (неотрицательность нормы),

2) x + y ≤ x + y (неравенство треугольника),

3)α x =|α | x .

Свойства 1) и 3) очевидны из определения нормы. Докажем неравенство треугольника. Для этого выведем сначала т.н. неравенство Коши-

Буняковского. В	силу аксиомы 4) скалярного произведения
(λx + y,λx + y) ≥ 0,	но (λx + y,λx + y) = λ2 (x, x) +2λ(x, y) +( y, y) ≥ 0 . Для

раскрытия скобок мы воспользовались аксиомами 1)-3). Поскольку неравен-

ство выполняется для всех λ , дискриминант квадратного трехчлена относительно λ неположителен, т.е. D = 4(x, y)2 −4(x, x) (y, y) ≤ 0 . Отсюда

(x, y)2 ≤ (x, x) ( y, y) = x2 y2 . После извлечения квадратного корня получа-

ем неравенство Коши-Буняковского

| (x, y) |≤

(14.2)

Вернемся к доказательству свойства 2)

нормы. Можно записать, что

x + y2 = (x + y, x + y) = (x, x) +2(x, y) +( y, y) ≤ x2 +2 x y + y2 = ( x+ y)2 ,

откуда после извлечения квадратного корня и следует неравенство треугольника. При выводе мы воспользовались соотношением (14.2).

Наличие скалярного произведения позволяет ввести в En понятие угла ϕ между векторами x, y En , а именно

cosϕ =	(x	, y)		.	(14.3)

	x		y

При этом в силу неравенства (14.2) для любых x, y					\| cosϕ \|≤1, т.е. вве-

денное определение угла корректно в действительном евклидовом пространстве. Заметим, что из (14.3) следует, что если (x, y) = 0 , то ϕ =π / 2 . В этом случае будем говорить, что векторы x и y ортогональны по аналогии с геометрическими векторами.

Определение. Система ненулевых векторов {xi }ik=1 из En называется

ортогональной, если (xi , xj ) = 0, i ≠ j .

Утверждение. Векторы ортогональной системы линейно независимы. Доказательство. В самом деле, пусть α1x1 +α2 x2 +... +αk xk =θ , тогда

можно записать, что (xj ,α1x1 +α2 x2 +... +αk xk ) = 0 для любого xj этой системы. Раскрывая скобки и учитывая ортогональность системы, получим, что (xj ,αj xj ) =αj xj 2 = 0 αj = 0, поскольку все векторы в системе ненуле-

вые. Значит, все коэффициенты αj в линейной комбинации равны нулю, что и означает, по определению, что векторы x1, x2 ,..., xk – линейно независимы.

Утверждение. Любая линейно независимая система может быть ортого-

нализована.

Доказательство.

Пусть имеется

k линейно

независимых

векторов

В качестве первого вектора ортогональной системы {e

возьмем

i=1

e1 = x1 .

Далее,

положим e2

=α1e1 + x2 .

Подберем

число

α1

так, чтобы

,e ) =α

,e ) +(e

, x

) = 0 .

Следовательно, α = −

(e1, x2 )

. Третий вектор

будем строить в виде линейной комбинации e3 = β1e1 + β2e2 + x3 . Коэффици-

енты	β1			и			β2	подберем,		исходя			из	требования	ортогональности
(e3,e1) = (e3,e2 ) = 0 .								Поскольку условие (e1,e2 ) = 0 уже выполнено, получим
(e ,e )	= β			e		2	+(x ,e ) = 0,		(e ,e ) = β			e	2 +(x ,e ) = 0 , откуда β			= −	(x3,e1)			,
						2											(x3,e1)

3 1			1	1			3 1		3 2		2	2		3 2	1			e	2
3 1			1	1			3 1		3 2		2	2		3 2	1			e	2
																		1
β2 = −	(x3,e2 )				.		Продолжая		этот	процесс, мы				выстраиваем ортогональную
β2 = −	2				.		Продолжая		этот	процесс, мы				выстраиваем ортогональную
		e
		2

систему в виде линейных комбинаций векторов данной системы. Описанный алгоритм называется процессом ортогонализации.

Определение. Вектор b En назовем нормированным, если b =1. Любой вектор евклидова пространства можно нормировать – умножить

его

на

т.н. нормирующий множитель

. Так, если

≠1, то

(a,a)

b =

уже имеет единичную норму

=1,

т.е. является нормированным.

Переход от вектора a к вектору b называется нормировкой вектора a .

Определение. Базис {ei }пространства En называется ортонормированным, если: 1) этот базис ортогонален; 2) все векторы этого базиса нормированы.

Утверждение. Любое пространство En обладает ортонормированным базисом.

Доказательство. Возьмем произвольный базис, подвергнем его процессу ортогонализации, а затем нормировке.

Пусть {ei }in=1 – ортонормированный базис в En . Выразим скалярное

произведение		двух	произвольных		векторов	этого	пространства через их
			n		n
координаты.		Пусть	x = ∑αiei ,	y	= ∑βiei ,	тогда
			i=1		i=1
n		n	n n		n
(x, y) = ∑αiei	∑βjej		= ∑∑αi βj (ei ,ej ) =∑αi βi , что совпадает с формулой (14.1).
i=1		j=1	i=1 j=1		i=1
Пример.		Найти ортонормированный базис,					порожденный векторами
x1 = (1,2,1) ,	x2 = (2,3,4) , x3 = (3,2,1) . Вычислим определитель матрицы пере-

хода Te→x к «базису» {x1, x2 , x3} от базиса e1 = (1,0,0) , e2 = (0,1,0), e3 = (0,0,1)

пространства E3 :			detTe→x =					1	2		3		=10 ≠ 0 {x1, x2 , x3} – базис.
								1	2		3
								2	3		2
								1	4		1
Положим f1 = x1 = (1,2,1),										f1		=			.
														6
														6
Далее, f		=α f			+ x		, где α			= −( f1, x2 ) = −1 2 +2 3+1 4 = −2 .
	2	1		1		2	1							f1		2	12 +22 +12
														f1		2	12 +22 +12

Тогда f2 = (0,−1,2),

β2 = −( f2 , x3 ) = 0 .

f2 2

	f		=		. Ищем f		= β f		+ β		f		+ x ,		гдеβ = −				( f1, x3 )			= −	4	,
		2		5

						3	1	1		2		2		3	1					f1	2		3

Отсюда					f3 = (5 / 3,−2 / 3,−1/ 3) ,									f2		=		/ 3.
																	30

Нормируя систему {f1, f2 , f3}, получим ортонормированный базис

g =	1		,	2	,	1	,	g		=	0,−	1	,	2	,	g =	5		,−		2	,−	1	.
					,		,	g		=	0,−		,		,	g =			,−			,−		.
									2							1
1		6		6 6					2			5 5				1		30		30			30
		6		6 6								5 5						30		30			30

Лекция 15

Пусть дано n-мерное действительное линейное пространство Vn , и пусть задано отображение A: Vn →Vn ,, т.е. для x Vn , Ax = y , вектор y Vn называется образом вектораx .

Определение. Отображение A называется линейным оператором, если:

1) A(x+y)=Ax +Ay x, y Vn ;

2) A(λx) = λ(Ax) x Vn , λ R .

Замечание. В этом разделе под оператором A мы понимаем только линейный оператор.

Утверждение. 1) Линейный оператор переводит любую линейную комбинацию векторов в линейную комбинацию (с теми же коэффициентами) образов этих векторов, т.е. A(α1x1 +... +αn xn ) =α1 Ax1 +...αn Axn ; 2) линейный

оператор переводит вектор θ (нулевой) в θ ;	3) A(−x) = −Ax .
Докажем пункт 2). Пусть y Vn –	произвольный вектор. Тогда
Aθ = A(0 y) = 0 Ay =θ .

Доказательство пункта 3). Действительно, A((−1) x) = (−1) Ax .

Примеры.

1.Тождественный оператор I x = x, x Vn

2.Нулевой оператор Оx =θ, x Vn .

3.Линейный оператор, переводящий вектор, исходящий из начала координат, в проекцию на какую-либо ось.

4.Ax =[a, x], где a = (α1,α2 ,α3 ) - фиксированный вектор в пространстве

R3 ; [a, x] – векторное произведение векторов в пространстве R3 .

В линейном пространстве Vn зафиксируем базис A:Vn →V {ei}in=1 . Тогда для x Vn имеем x =α1e1 +... +αnen . Любой линейный оператор A, действующий в пространстве Vn , однозначно определяется заданием образов

Ae1,..., Aen всех	векторов фиксированного базиса. Действительно, пусть
n	n
x = ∑αiei , тогда	Ax = ∑αi Aei , а величины Aei уже определены.
i=1	i=1

Утверждение. Для любого упорядоченного набора v1,...,vn Vn единственный линейный оператор A:Vn →Vn ,такой что Aei = vi .

Это означает взаимно однозначное соответствие между A :Vn →Vn , и набором векторов {v1,...,vn} из Vn . Очевидно, что любой vj из этого набора

записывается в

базисе

{ei}in=1

виде

v j

= ∑αijei , j =1,...,n , где числа

i=1

- координаты векторов v

в базисе {e }n

. Составим из коэффициентов

i=1

...

матрицу A =

α21

α22

α2n

, здесь j

– столбец матрицы A состоит из

... ...

...

αn1

αn2

...

αnn

координат вектора vj .

Поскольку

{vj} произвольны, то

матрица

A произвольна

dim A = n ×n . Таким образом, мы получили взаимно однозначное соответствие при фиксированном базисе между линейными операторами и матрицами.

Определение. В этом случае говорят, что матрица A={αij} – матрица

линейного оператора A в базисе {e }n			.
		i i=1
Если разложить вектор Ae		по базису {e }n		, то будем иметь
	k		i i=1
	Aek =α1k e1 +α2k e2 +... +αnk ek ,k =1,...,n,				(15.1)
т.е.	Ae = eA, где Ae = (Ae1,..., Aen ), e = (e1,e2 ,...,en ).				(15.2)
Пусть	A – матрица линейного оператора.

Вопрос. Как найти координаты образа вектора x Vn при этом преобразованииA?

n	n
Итак, пусть x = ∑γiei ,γi известны,	Ax = y, y = ∑βiei . Тогда
i=1	i=1

Ax =γ1 Ae1 +... +γn Aen = ∑βk ek . Используя формулу (15.1), получаем, что

k=1

Ax = ∑γi Aei =

∑γi (α1ie1 +... +αnien ) = ∑γi ∑αkiek = ∑βk ek ,

i=1

k=1

т.е.

∑(∑γiαki ) = ∑βk ek .

В итоге получаем формулу

k=1

i=1

k=1

(β ,β

,...,β

= A(γ

,...,γ

)t .

(15.3)

Пример. Пусть задано V3

и определена матрица линейного оператора A

−2

в виде:

A =

. Задан вектор a = 5e +e

−2e . Найдем координаты

−4

b – образа этого вектора при нашем преобразовании. Согласно формуле (15.3), получим, что

−2		1	0 5		−9
b = Aa =	1	3	2	1	=	4	, т.е.	b = −9e +4e +24e .
								1	2	3
	6	−4 1		−2		24
	6	−4 1		−2		24

Преобразование матрицы линейного оператора при изменении базиса.

Пусть имеется пространство Vn и два базиса {ei} и { fi} и матрица перехода T от базиса {ei} к базису { fi}, т.е. f = eT . И пусть оператор D задается матрицей A и B соответственно в базисе {ei} и { fi}, тогда, ввиду (15.1),(15.2), De = eA, D f = fB . Отсюда получаем, что D f = fB = (eT )B = e(TB), но

D f = D(eT) = (De)T = (eA)T = e(AT), e(TB) = e(AT). Поскольку векторы ei

линейно независимы, то получаем, что TB = AT ,или

B = T −1 AT , A = TBT −1,detT =		T		≠ 0.	(15.4)

Пример. Пусть задан линейный оператор Ax =[a, x], где a = (α1,α2 ,α3 ) -

фиксированный вектор в пространстве R3 , [a, x] – означает векторное про-

изведение векторов (см. лекцию 8) пространства R3 . Найдем матрицу опера-

<<< < Предыдущая 1 2 3 4 5 67 / 97 8 9 > Следующая >>>

Соседние файлы в предмете Высшая математика

#
01.06.20246.08 Mб1L_D_Kudryavtsev_Kurs_matimaticheskogo_analiza_Tom_2.pdf
#
01.06.20242.46 Mб1L_D_Kudryavtsev_Kurs_matimaticheskogo_analiza_Tom_3.pdf
#
01.06.20241.39 Mб10вышмат полезно.pdf
#
01.06.2024482.88 Кб3кр по алегебре.pdf
#
01.06.20245.41 Mб72лекции вышмат.pdf
#
01.06.20241.34 Mб2линейная алгебра и агалитич геом.pdf