
линейная алгебра и агалитич геом
.pdf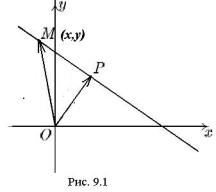
([a |
,b |
],c) = |
|
α1 |
α2 |
α3 |
|
. |
(8.3) |
|
|
||||||||
|
β1 |
β2 |
β3 |
|
|||||
|
|
|
|
γ1 |
γ2 |
γ3 |
|
|
|
Из формулы (8.3) и свойств определителей следует, что ([a,b],c) = (a,[b,c]) , |
|||||||||
поэтому в дальнейшем смешанное произведение будем обозначать просто
a b c . Кроме того, при циклической |
|
перестановке |
|
сомножителей сме- |
|
|
|
|
|
||
шанное произведение не меняется: a b c = b c a = c a b , а при пере-
становке соседних сомножителей меняет знак. Оно дистрибутивно и однородно по каждому сомножителю: например,
|
|
|
|
|
|
|
|
|
(a1 |
+ a2 ) b c = a1 |
b c + a2 |
b c ; |
(λa) b c = λ (a b c) . |
||||
Раздел IV. Уравнения первого порядка и их геометрические образы
Лекция 9
Уравнение вида F(x, y) = 0 называется уравнением линии L , расположенной в плоскости Oxy , если ему удовлетворяют декартовы координаты любой точки, принадлежащей линии L , и не удовлетворяют координаты никаких других точек. Так, например, уравнение x2 + y2 −1 = 0 определяет окружность единичного радиуса с центром в начале координат.
Теорема. Произвольная прямая, принадлежащая плоскости Oxy , задается уравнением первого порядка относительно декартовых координат x и y .
|
|
|
|
|
|
Доказательство. Проведем из начала координат вектор OP , перпенди- |
|||||
кулярный к данной прямой (рис. 9.1). |
|
|
|
|
|
|
Тогда произвольная точка |
M прямой об- |
|||
ладает свойством |
|
|
|
||
пр OM = p , |
где p =|OP | – |
||||
|
|
|
OP |
|
|
расстояние от начала координат до прямой. Но |
|||||
|
|
|
|
|
|
OM |
OP =|OP | пр OM = p2 |
. Если OP ={α,β}, |
|||
|
|
OP |
|
|
|
|
Значит, уравнение |
||||
то OM OP =αx + β y = p2 . |
|||||
|
|
40 |
|
|
|
прямой имеет вид αx + β y − p2 = 0 . Это линейное уравнение. Его можно ум-
ножить на любое отличное от нуля число, тогда получим |
Ax + By +C = 0 |
|
(т.н. общее уравнение прямой на плоскости). |
|
|
Из доказательства ясен смысл коэффициентов A и B , |
пропорциональ- |
|
ных координатам α и β вектора OP , а именно: |
|
|
вектор N ={A, B} перпендикулярен |
прямой, за- |
|
данной уравнением Ax + By +C = 0 . |
Этот вектор |
|
называется нормальным вектором прямой.
Пусть заданы две прямые A1x + B1 y +C1 = 0, A2 x + B2 y +C2 = 0. Угол ϕ между ними равен углу
между их нормальными векторами N1 и N2 , но угол между прямыми выбирается меньший из двух смежных, т.е. не превосходящий прямого, а угол между векторами может быть тупым. Чтобы получить ϕ ≤π / 2, в формуле (8.1) возьмем числитель по модулю:
|
ϕ = arccos |
|
| A1 A2 + B1B2 | |
|
|
|
. |
|
|
(9.1) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
A2 + B2 |
A2 + B2 |
|
|
|||||||||||
|
|
|
1 |
1 |
|
2 |
|
2 |
|
|
|
|
|
||
Условие перпендикулярности прямых имеет вид A1 A2 + B1B2 |
= 0, условие |
||||||||||||||
параллельности следует из того, что N1 |
N2 |
|
|
A1 |
= |
B1 |
. Если эти отноше- |
||||||||
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
A |
B |
|
||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
ния равны C1 , то прямые совпадают. |
|
|
|
|
|
|
|
|
|
|
|
|
|||
C2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Расстояние |
от произвольной точки M0 (x0 , y0 ) плоскости |
до прямой |
|||||||||||||
Ax + By +C = 0 можно вычислить по формуле |
|
|
|
|
|
|
|
|
|
|
|||||
|
d = |
| Ax0 + By0 |
+C | |
. |
|
|
(9.2) |
||||||||
|
|
A2 + B2 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
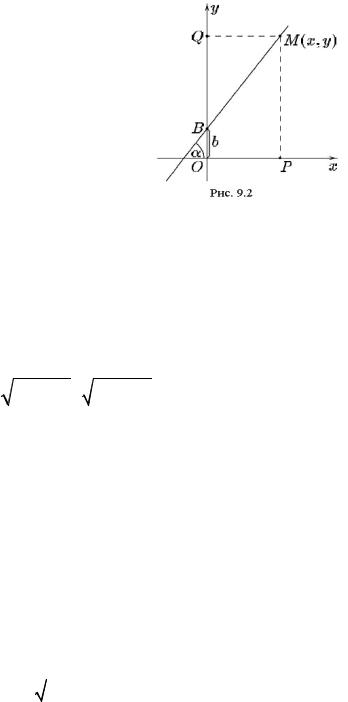
Если B ≠ 0 |
(т.е. прямая не параллельна оси Oy ), то общее уравнение |
||||||||||||||
можно переписать в виде y = −(A / B)x −(C / B) |
или |
y = kx +b . Последнее |
|||||||||||||
уравнение называется уравнением прямой с угловым коэффициентом k , ко-
41
торый равен tgα , где α – угол наклона прямой к положительному направлению оси Ox (рис. 9.2). Угол между прямыми можно рассчитать по формуле
ϕ = arctg |
|
k1 −k2 |
|
, а |
условия параллельности и перпендикулярности через |
||
|
|||||||
|
1+k k |
2 |
|
|
|
|
|
|
1 |
|
|
|
|
||
угловые коэффициенты прямых соответственно выражаются так: k1 = k2 |
и |
||||||
k1 k2 = −1. |
|
|
|
|
|
||
Уравнение вида |
F(x, y, z) = 0 называется уравнением поверхности |
S , |
|||||
если ему удовлетворяют декартовы координаты любой точки, принадлежащей поверхности S , и не удовлетворяют координаты никаких других точек. К примеру, уравнение x2 + y2 + z2 −1 = 0 определяет сферу единичного радиуса с центром в начале координат.
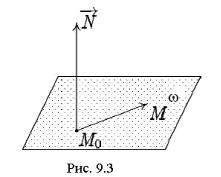
Пусть в пространстве дана плоскость ω и
выбрана декартова система |
координат. |
Пусть |
|
M0 (x0 , y0 , z0 ) – некоторая точка плоскости |
ω и |
||
вектор |
N ={A, B,C} – произвольный ненулевой |
||
вектор, |
перпендикулярный |
нашей плоскости |
|
(такой вектор называется нормалью к плоскости, рис. 9.3).
|
|
|
|
Точка M (x, y, z) ω M0M |
N |
(M0M , N ) = 0 |
. Выражая скалярное |
произведение через координаты, получим |
|
||
A(x − x0 ) + B( y − y0 ) +C(z − z0 ) = 0. |
(9.3) |
||
Это – уравнение произвольной плоскости, проходящей через заданную точку M0 . Оно является линейным относительно координат текущей точки M плоскости ω. Итак, справедливо следующее утверждение.
Теорема. Уравнение произвольной плоскости в некоторой декартовой системе координат имеет вид Ax + By +Cz + D = 0 (общее уравнение плоскости).
Общее уравнение может быть неполным, когда один или несколько коэффициентов (но только не A, B и C одновременно) равны нулю. Так, при
42
A = 0 плоскость параллельна оси Ox , при D = 0 она проходит через начало координат, а при A = D = 0 , следовательно, проходит через ось Ox .
Для пары плоскостей A1x + B1 y +C1z + D1 = 0 , A2 x + B2 y +C2 z + D2 |
= 0 |
можно сформулировать условие перпендикулярности A1 A2 + B1B2 +C1C2 |
= 0 |
и условие параллельности: A1 = B1 = C1 .
A2 B2 C2
Угол между плоскостями (понимаемый как меньший из двух смежных двугранных углов) задается формулой
ϕ = arccos |
|
|
|
| A1 A2 + B1B2 +C1C2 | |
|
|
|
. |
|
|
(9.4) |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
A2 |
+ B2 +C2 |
A2 |
+ B2 +C2 |
|
|
|
|||||||||||||||
|
1 |
1 |
1 |
2 |
2 |
2 |
|
|
|
|
|
|
|
|
|
||||||
Расстояние от точки M0 (x0 , y0 , z0 ) |
до плоскости Ax + By +Cz + D = 0 |
вы- |
|||||||||||||||||||
числяется по формуле, аналогичной (9.2): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
d = |
| Ax0 + By0 +Cz0 |
+ D | |
. |
|
|
|
|
|
|
(9.5) |
|
||||||||||
|
|
|
A2 + B2 +C2 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Составим уравнение плоскости, проходящей через точку |
M0 (x0 , y0 , z0 ) |
||||||||||||||||||||
параллельно двум неколлинеарным векторам a ={α ,α |
2 |
,α |
} и b |
={β , β |
2 |
, β |
}. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
3 |
|
1 |
|
3 |
|
||
Согласно свойствам векторного произведения, в качестве нормали можно взять N =[a,b]. Тогда уравнение плоскости в векторной форме имеет вид
|
|
|
|
|
{x − x0 , y − y0 , z − z0}. |
|
||
(M0M , N ) = 0 , или |
M0M |
a b = |
0 , где M0M = |
По фо р- |
||||
муле (8.3) имеем |
|
|
|
|
|
|
|
|
|
|
|
x − x0 |
y − y0 |
z − z0 |
|
= 0 . |
(9.6) |
|
|
|
|
|||||
|
|
|
α1 |
α2 |
α3 |
|
||
|
|
|
β1 |
β2 |
β3 |
|
|
|
Из уравнения (9.6) легко получить уравнение плоскости, проходящей че- |
||||||||
рез три данные точки M1(x1, y1, z1), |
M2 (x2 , y2 , z2 ) , |
M3(x3, y3, z3 ) , не лежащие |
||
|
|
|
|
|
на одной прямой. Именно, в качестве векторов a |
и b можно взять |
M1M2 |
и |
|
|
M1 . Тогда получим: |
|
|
|
M1M3 , а в качестве точки M0 взять |
|
|
||
|
43 |
|
|
|

x − x1 x2 − x1 x3 − x1
y − y1 y2 − y1 y3 − y1
z − z1
z2 − z1 = 0. (9.7) z3 − z1
Определение. Пучком плоскостей называется множество всех плоско-
стей, проходящих через данную прямую L . |
|
|
|
|
|
|||
Теорема. |
Пусть |
две различные |
плоскости |
A1x + B1 y +C1z + D1 = 0 и |
||||
A2 x + B2 y +C2 z + D2 = 0 |
принадлежат некоторому |
пучку. Тогда |
уравнение |
|||||
любой другой |
плоскости этого |
пучка можно |
записать |
в виде |
||||
λ(A1x + B1 y +C1z + D1) + µ(A2 x + B2 y +C2 z + D2 ) = 0, |
где λ |
и |
µ |
– некоторые |
||||
числа. |
|
|
|
|
|
|
|
|
Доказательство. |
Покажем, что коэффициенты при x , |
y |
и z |
в уравне- |
||||
нии пучка не могут обратиться в ноль одновременно. Действительно, если
λA1 + µA2 = λB1 + µB2 = λC1 + µC2 = 0 , то A1 / A2 = B1 / B2 = C1 / C2 , т.е. плоско-
сти параллельны, но, по условию, они различны и проходят через прямую L , значит, не могут быть параллельными. Итак, это линейное уравнение определяет плоскость. Очевидно, все точки прямой L удовлетворяют этому уравнению при любых λ и µ плоскость проходит через L . Любую плоскость
пучка |
можно |
выделить, |
задав |
принадлежащую ей |
точку |
M *(x*, y*, z* ) , |
||||
не |
лежащую |
на |
прямой |
L , |
тогда |
из |
равенства |
|||
λ(A x* + B y* +C z* + D ) + µ(A x* + B y* +C |
z* + D ) = 0 |
можно |
найти отно- |
|||||||
1 |
1 |
1 |
1 |
2 |
2 |
2 |
|
2 |
|
|
шение λ / µ (или µ / λ ), отвечающее выделенной плоскости пучка.
Лекция 10
Линию в пространстве можно рассматривать как непустое пересечение двух поверхностей. Таким образом, система двух уравнений с тремя переменными
F (x, y, z) = 0, |
(10.1) |
1 |
|
F2 (x, y, z) = 0 |
|
44 |
|
|
|
|
2 |
|
2 |
|
2 |
|
может определять некоторую линию |
L . Например, система |
x |
|
+ y |
|
+ z |
|
=1, |
|
|
|
x + y + z = 0 |
|||||
задает единичную окружность с центром в начале координат, лежащую в плоскости x + y + z = 0.
Однако, система вида (10.1) может определять не только линию, но и отдельные точки или даже поверхности. Система (10.1) определяет линию тогда и только тогда, когда ее общее решение записывается следующим образом:
x =y =z =
x(t),
y(t), (10.2) z(t).
Эти соотношения называются параметрическими уравнениями линии в пространстве.
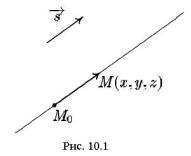
Пусть дана некоторая прямая L и любая точка M0 (x0 , y0 , z0 ) L . Далее,
пусть s ={l,m,n}– произвольный ненулевой вектор, лежащий на данной прямой или параллельный ей. Такой вектор называется направляющим вектором прямой (рис.10.1). Пусть M (x, y, z) L – текущая (произвольная) точ-
ка. Тогда |
M0M s , но |
коллинеарные векторы |
||||||||
имеют |
|
|
пропорциональные |
координаты: |
||||||
|
x − x0 |
|
= |
y − y0 |
= |
z − z0 |
. |
Мы получили канониче- |
||
|
l |
|
|
m |
|
n |
|
|
||
ские уравнения прямой в пространстве. По сути, это система вида (10.1). Приравняем каждую из дробей в канонических уравнениях некоторому числу t , тогда получим параметрические уравнения этой прямой:
x = x0 +lt, |
|
|
|
+mt, |
(10.3) |
y = y0 |
||
|
+nt. |
|
z = z0 |
|
|
45

Прямую в пространстве также можно рассматривать как пересечение
двух непараллельных плоскостей, т.е. система вида |
|
A x + B y +C z + D = 0, |
|||
|
1 |
1 |
1 |
1 |
|
|
A2 x + B2 y +C2 z + D2 = 0, |
||||
где коэффициенты A1, B1,C1 непропорциональны коэффициентам |
|
A2 , B2 ,C2 , |
|||
также определяет прямую. Чтобы перейти от такой записи к параметрическим уравнениям (10.3), достаточно найти общее решение этой системы, например, методом Гаусса (см. лекцию 3). Можно поступить иначе: в качестве направляющего вектора взять векторное произведение нормалей пересекающихся плоскостей, т.е. s =[N1, N2 ], а точку M0 выбрать как любое частное
решение системы (например, положить одну из переменных равной нулю). |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x − y +3z +7 = 0, |
|
||||
|
|
Пример. Привести к каноническому виду прямую |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3x + y − z −2 = 0. |
|
||||
|
|
N1 ={2, |
−1,3}, |
N2 ={3,1,−1}, |
|
|
i |
j |
k |
|
|
|
|
||||||
|
|
|
|
||||||||||||||||
|
|
[N1 |
, N2 ] = |
|
2 |
−1 |
3 |
|
= −2i +11 j +5k , |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
−1 |
|
|
|
|
|
|
|
s ={−2,11,5}. |
|
z = 0, |
|
|
|
|
|
|
x = −1, |
|||||||
т.е. |
Положим в системе |
|
|
тогда |
получим |
||||||||||||||
|
y = 5 |
M0 (−1,5,0) . Составляем канонические уравнения данной прямой: |
|||||||||||||||||
|
x +1 |
= |
y −5 |
|
= |
z |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
−2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
11 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Заметим, что для составления уравнений прямой, проходящей через две |
|||||||||||||||||
заданные точки |
M1(x1, y1, z1) |
и M2 (x2 , y2 , z2 ) , достаточно в качестве направ- |
|||||||||||||
|
|
|
|
|
|
l = x2 |
− x1 , m = y2 − y1 , |
n = z2 − z1 . |
|||||||
ляющего вектора взять s |
= M1M2 , т.е. |
||||||||||||||
Рассмотрим две прямые: |
|
|
|
|
|
|
|
|
|
||||||
|
x − x1 |
= |
y − y1 |
= |
z − z1 |
(L ) |
и |
|
x − x2 |
= |
y − y2 |
= |
z − z2 |
(L ). |
|
|
|
|
|
|
|
|
|||||||||
|
l1 |
m1 |
n1 |
1 |
|
|
l2 |
m2 |
2 |
||||||
|
|
|
|
|
n2 |
||||||||||
Условия параллельности и перпендикулярности прямых таковы:
L1 L2 s1 s2 l1 = m1 = n1 ,
l2 m2 n2
46
L1 L2 s1 s2 (s1, s2 ) = 0 l1l2 +m1m2 +n1n2 = 0 .
Угол между прямыми можно найти по формуле
ϕ = arccos |
|
|
| l1l2 + m1m2 + n1n2 | |
|
|
. |
||||
|
|
|
|
|
|
|
|
|
||
l2 |
+ m2 |
+ n2 |
|
l2 |
+ m2 |
+ n2 |
||||
1 |
1 |
1 |
|
2 |
2 |
2 |
|
|
||
Две прямые в пространстве могут быть параллельными, пересекаться или скрещиваться. В первых двух случаях они принадлежат одной плоско-
сти. Условие принадлежности двух прямых L1 и L2 одной плоскости может
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
быть записано, исходя из компланарности векторов s1 |
, |
s2 |
и M1M2 |
: |
|||||||||||||||||||||
|
|
|
|
|
|
l1 |
|
|
m1 |
|
n1 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
s1 |
s2 |
M1M2 |
= |
|
l2 |
|
|
m2 |
|
n2 |
|
= 0 . |
|
|
||||||||||
|
|
|
|
|
|
|
|
x2 − x1 |
|
y2 − y1 |
|
z2 − z1 |
|
|
|
|
|
|
|
||||||
Если прямые не принадлежат одной плоскости, они являются скрещи- |
|||||||||||||||||||||||||
вающимися. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим |
теперь |
прямую |
|
x − x0 |
= |
|
y − y0 |
|
= |
z − z0 |
|
|
|
|
|
||||||||||
|
|
m |
|
n |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|||||
(L) и плоскость |
Ax + By +Cz + D = 0 |
|
(ω) . |
Условия |
|
|
|
|
|||||||||||||||||
параллельности и перпендикулярности прямой и |
|
|
|
|
|||||||||||||||||||||
плоскости легко сформулировать на языке их на- |
|
|
|
|
|||||||||||||||||||||
правляющего вектора и нормали: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
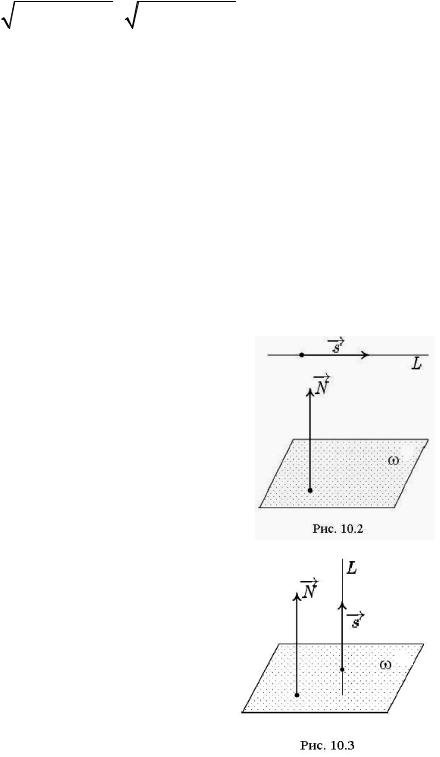
L ω N s |
(N, s) = 0 Al + Bm +Cn = 0 |
|
|
|
|
||||||||||||||||||||
(рис.10.2), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
B |
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
L ω N s |
|
|
= |
|
= |
|
(рис. 10.3). |
|
|
|
|
||||||||||||||
l |
m |
n |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Угол ϕ |
между |
прямой |
|
L |
и |
плоскостью |
|
|
|
|
|||||||||||||||
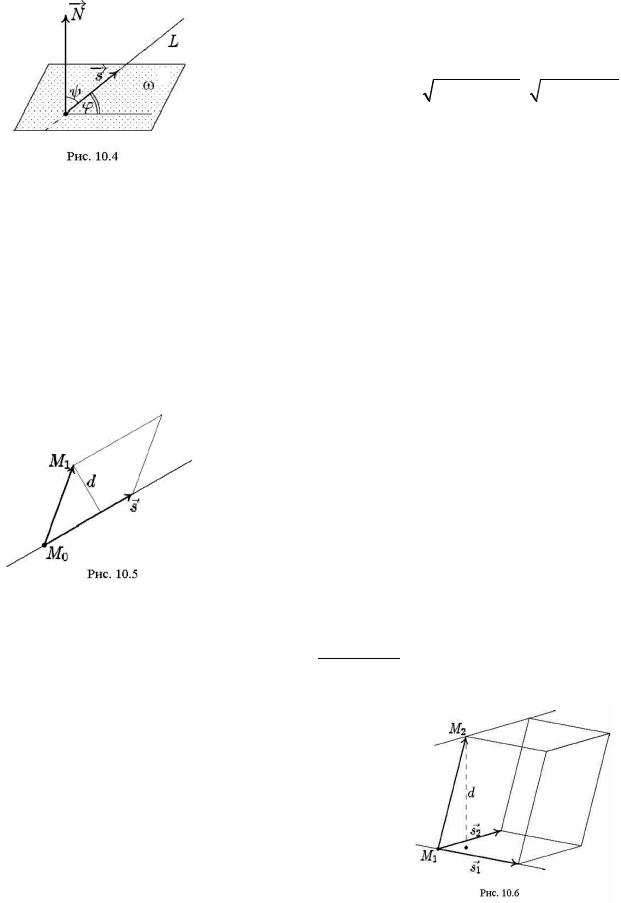
ω – это угол между прямой и ее проекцией на эту плоскость. Он в сумме с углом ψ между направляющим вектором пря-
мой s и нормалью N
47
|
к плоскости составляет π / 2 (рис. 10.4). Отсюда |
||||||||||
|
sinϕ = cosψ , |
но |
|
|
|
|
|
|
|||
|
cosψ = |
| (N,s) | |
ϕ = arcsin |
|
|
| Al + Bm +Cn | |
|
|
. |
||
|
N s |
|
|
|
|
|
|
|
|||
|
|
|
|
A2 + B2 +C2 l2 +m2 |
+n2 |
||||||
|
Сформулируем условие |
принадлежности |
|||||||||
|
прямой |
данной |
|
плоскости: |
|||||||
|
Al + Bm +Cn = 0, |
Первое соотношение системы выражает |
|||||||||
L ω |
|
||||||||||
Ax0 + By0 +Cz0 + D = 0. |
|
|
|
|
|
|
|
|
|
|
|
параллельность прямой и плоскости, второе — принадлежность некоторой точки прямой данной плоскости.
Выведем теперь формулу, по которой можно рассчитать расстояние от
произвольной |
точки |
|
M1(x1, y1, z1) |
|
|
пространства |
до |
прямой |
|||||||||
|
|
|
x − x0 |
= |
y − y0 |
|
= |
z − z0 |
. |
Если построить на векто- |
|||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
l |
m |
|
|
|
n |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
рах M0M1 |
и |
|
s , как на сторонах, параллелограмм, |
||||||||||||
|
|
искомое расстояние |
d |
будет его высотой, прове- |
|||||||||||||
|
|
денной к стороне длиной | s | (рис. 10.5). Площадь |
|||||||||||||||
|
|
параллелограмма численно равна длине векторно- |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
го произведения [M0M1 |
, s] , отсюда |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
[M0M1, s] |
|
|
|
|
|||||
|
|
|
|
|
d |
= |
|
|
|
|
|
|
|
. |
|
|
(10.4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
| s | |
|
|
|
|
|
|
|
Расстояние между скрещивающимися пря- |
|
|
|
||||||||||||||
мыми найдем, исходя из геометрического смысла |
|
|
|
||||||||||||||
смешанного произведения. Именно, объем V па- |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
раллелепипеда, построенного на векторах s1 , |
s2 |
, |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M1M2 как на ребрах, |
численно равен модулю |
|
|
|
|||||||||||||
смешанного произведения этих векторов. Здесь
48

s1 ={l1,m1,n1}, s2 ={l2 ,m2 ,n2} – направляющие векторы прямых, а M1(x1, y1, z1) и M2 (x2 , y2 , z2 ) – их точки. Расстояние между скрещивающими-
ся прямыми равно высоте d этого параллелепипеда: d = V |
, где площадь ос- |
||||||||
|
|
|
|
|
|
S |
|
|
|
нования S численно равна длине векторного произведения |
|
||||||||
[s1 |
, s2 |
] (рис. 10.6). |
|||||||
Таким образом: |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
||||
|
|
s1 |
s2 M1M2 |
|
|
|
|
||
d = |
|
|
|
|
|
. |
|
|
(10.5) |
|
|
|
|
|
|||||
|
|
|
|[s1 |
, s2 |
]| |
|
|
|
|
Раздел V. Уравнения второго порядка и их геометрические образы
Лекция 11
В лекции 9 мы выяснили, что уравнение первой степени Ax + By +C = 0 определяет прямую линию на плоскости. Перейдем теперь к рассмотрению геометрических образов алгебраического уравнения второй степени относительно x и y : Ax2 + Bxy +Cy2 + Dx + Ey + F = 0. Для упрощения общего уравнения воспользуемся преобразованиями поворота и параллельного переноса (см. лекцию 7). Поворотом системы устраняем слагаемое, содержащее произведение координат; затем параллельным переносом (с точки зрения алгебры это означает выделение полных квадратов) устраняем линейные слагаемые. Поясним этот алгоритм конкретным примером.
Пример. Упростить уравнение 52x2 −72xy +73y2 −100x +50y −50 = 0. Произведем поворот системы на угол α относительно начала координат. Сделаем подстановку x = x′cosα − y′sinα , y = x′sinα + y′cosα (см. лек-
цию 7). После приведения подобных слагаемых получим
x′2 (52cos2 α −72cosαsinα +73sin2 α) + x′y′(72sin2 α +42sinαcosα −72cos2 α) +
+y′2 (52sin2 α +72cosαsinα +73cos2 α) + x′(50sinα −100cosα) + y′(50cosα +100sinα) −50 =0.
49
