
линейная алгебра и агалитич геом
.pdfется нетривиальной, если ее коэффициенты не все равны нулю, в противном случае линейная комбинация называется тривиальной.
Определение. Векторы называются линейно независимыми, если только тривиальная комбинация этих векторов равна нулевому вектору:
α1 a1 +α2 a2 +... +αn an =θ α1 = α2 |
= ... = αn = 0 . |
|
|
|
|
||||||||||||
Векторы называются линейно зависимыми, если существует их нетриви- |
|||||||||||||||||
альная комбинация, равная нулевому вектору: |
|
|
|
|
|
|
|
|
|
||||||||
α ,α |
2 |
,...,α |
n |
; α2 |
+α2 |
+... +α2 |
≠ 0; |
α a +α |
2 |
a |
2 |
+... +α |
n |
a |
n |
=θ . |
|
1 |
|
1 |
2 |
n |
|
1 1 |
|
|
|
|
|
||||||
Очевидно, что если среди векторов |
a1,a2 ,...,an |
имеется хотя бы один нуле- |
|||||||||||||||
вой, то эти векторы линейно зависимы. |
|
|
|
|
|
|
|
|
|
|
|||||||
Утверждение. Совокупность векторов, содержащая линейно зависимую подсистему, сама является линейно зависимой. (Это очевидно, ведь по условию уже существует нетривиальная комбинация векторов подсистемы, равная нулю. При остальных векторах совокупности достаточно выбрать нулевые коэффициенты, комбинация все равно останется нетривиальной и равной нулевому вектору.)
Теорема. Необходимым и достаточным условием линейной зависимости
двух векторов является их коллинеарность. |
|
|
|
|
|
|
Доказательство. 1) Пусть векторы a |
и b |
линейно |
зависимы, т.е. |
|||
αa + βb =θ . Если, для определенности, α ≠ 0 |
|
|
β |
|
|
|
, то a = − |
α |
b |
a b (по оп- |
|||
|
|
|
|
|
|
|
ределению умножения вектора на число). 2) Если же дано, что a b , то или один из векторов нулевой, что влечет их линейную зависимость, или они оба ненулевые, но при этом связаны соотношением a = µb или a − µb =θ , а эта линейная комбинация векторов a и b нетривиальна (коэффициент при a равен 1). Значит, векторы a и b линейно зависимы.
Определение. Векторы называются компланарными, если они лежат в одной или в параллельных плоскостях.
30
Теорема. Необходимым и достаточным условием линейной зависимости
трех векторов является их компланарность. |
|
|
|
|
||||||
Доказательство. |
1) Пусть три вектора a , b и c линейно зависимы. То- |
|||||||||
гда α, β и γ |
такие, |
что αa + βb +γ c =θ , |
причем α2 + β2 +γ 2 ≠ 0 . Пусть |
|||||||
|
α |
β |
′ |
′ |
′ |
|
|
′ |
|
|
γ ≠ 0. Тогда c = − γ |
a |
− γ b= |
a |
+b , где |
a |
a , |
b |
b . Из правила параллело- |
||
грамма следует, что |
c лежит в плоскости параллелограмма, построенного на |
|||||||||
|
|
|
|
векторах a |
и b, а значит, все три этих вектора |
|||||
|
|
|
|
являются компланарными. 2) Пусть векторы a , |
||||||
|
|
|
|
b |
и c компланарны. Если какие-либо два из |
|||||
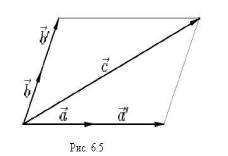
них коллинеарны, то все три линейно зависимы согласно утверждению этой лекции. Если же никакие два из этих векторов не коллинеарны, то перенесем их на одну
плоскость и приведем к общему началу. Проведем через конец вектора c
прямые, параллельные векторам a |
и b |
до пересечения с прямыми, на кото- |
||||||||
рых лежат векторы a и b. Получится |
параллелограмм (рис. 6.5). Вектор c |
|||||||||
является |
диагональю |
|
этого |
|
параллелограмма, |
следовательно, |
||||
|
′ |
′ |
|
|
|
|
|
|
, но из трех коэффициентов λ , µ , −1 |
|
c = a |
+b |
= λa + µb, или λa + µb |
−c =θ |
|||||||
один заведомо отличен от нуля. Следовательно, векторы a , |
b и c линейно |
|||||||||
зависимы.
Теорема. Любые четыре вектора в пространстве линейно зависимы. Приведем схему доказательства. Если среди четырех векторов есть три
компланарных, утверждение очевидно. Если никакие три из этих векторов не компланарны, то приведем их все к одному началу. Три некомпланарных вектора лежат на ребрах параллелепипеда, диагональю которого является четвертый вектор. Следовательно, он может быть представлен в виде суммы векторов, коллинеарных остальным трем векторам, то есть выражается в виде их линейной комбинации. Значит, все четыре вектора линейно зависимы.
31
Лекция 7
Определение. Два линейно независимых упорядоченных вектора a и b образуют базис на плоскости, если любой вектор c этой плоскости можно представить в виде их линейной комбинации, т.е. α,β такие, что
c =αa + βb .
Определение. Три линейно независимых упорядоченных вектора a , b и c образуют базис в пространстве, если любой вектор d пространства можно представить в виде d =αa + βb +γ c .
Равенство d =αa + βb +γ c называется разложением вектора d по бази-
су a , b, c , а числа α, β,γ — координатами вектора d в этом базисе. Очевидно (см. теоремы лекции 6), что на плоскости базисом являются любые два неколлинеарных вектора этой плоскости, а в пространстве – любая тройка некомпланарных векторов. Координаты вектора относительно заданного ба-
зиса определяются однозначно. Равенство |
d =αa + βb +γ c |
можно записы- |
вать в символическом виде d ={α, β,γ}. |
|
|
Теорема. Пусть в некотором базисе |
a , b, c заданы |
d1 ={α1, β1,γ1}, |
d2 ={α2 , β2 ,γ2}. Тогда d1 +d2 ={α1 +α2 , β1 + β2 ,γ1 +γ2}; λd1 ={λα1,λβ1,λγ1}.
Доказательство. λd1 = λ (α1a + β1b +γ1c)= (λα1)a +(λβ1)b +(λγ1)c ;
d1 +d2 = (α1a + β1b +γ1c)+(α2 a + β2 b +γ2 c)= (α1 +α2 )a +(β1 + β2 )b +(γ1 +γ2 )c .
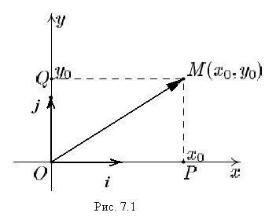
Базис из двух взаимно перпендикулярных единичных векторов плоскости i , j с началом в фиксированной точ-
ке O порождает декартову прямоуголь-
ную систему координат. Точка O назы-
вается началом координат, а координатные оси Ox и Oy , направленные
так же, как векторы i и j соответствен-
32
но, называются осью абсцисс и осью ординат (рис. 7.1). Координаты точки
M определим как координаты вектора OM в базисе |
i , j , т.е. если |
OM = x0 i + y0 j , то говорят, что точка M имеет абсциссу x0 |
и ординату y0 , и |
записывают M (x0 , y0 ). Длина вектора OM может быть найдена по теореме
|
|
|
|
|
|
Пифагора: OM = OP2 +OQ2 = x |
2 + y 2 |
. Заметим, что координаты вектора |
|||
0 |
0 |
|
|||
равны проекциям этого вектора на координатные оси. Если в выбранной системе координат заданы две точки M1(x1, y1) и M2 (x2 , y2 ), то координаты век-
тора M1M2 = OM2 −OM1 согласно предыдущей теореме можно найти, вычислив разность соответствующих координат конца и начала этого вектора:
M1M2 |
={x2 − x1, y2 − y1}, |
откуда |
расстояние |
между точками |
равно |
|||||||||||
M |
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
= (x |
2 |
− x )2 +( y |
2 |
− y )2 . |
|
|
|
|
|
|
|||||
1 |
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
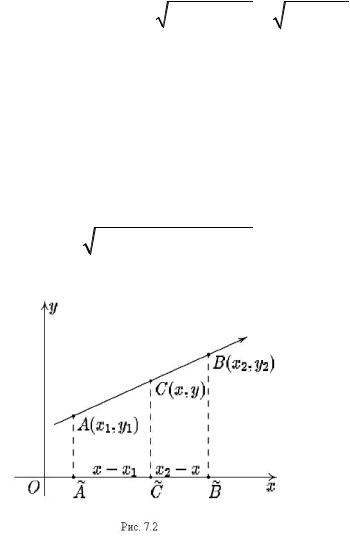
Перейдем теперь к задаче о делении |
||||
|
|
|
|
|
|
|
|
|
|
|
отрезка в заданном отношении. Пусть на |
|||||
|
|
|
|
|
|
|
|
|
|
|
плоскости |
заданы |
точки |
A(x1, y1) и |
||
|
|
|
|
|
|
|
|
|
|
|
B(x2 , y2 ) . Проведем через эти точки на- |
|||||
|
|
|
|
|
|
|
|
|
|
|
правленную ось (рис. 7.2). Пусть C(x, y) |
|||||
|
|
|
|
|
|
|
|
|
|
|
– |
точка на этой оси т |
акая, |
что |
AC = λ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
CB |
|
|
|
|
|
|
|
|
|
|
|
Параметр λ может принимать любые |
|||||
|
|
|
|
|
|
|
|
|
|
|
значения, кроме −1. |
При λ [0,+∞) точ- |
||||
ка C находится на отрезке AB , при λ (−∞,−1) точка C находится вне от- |
||||||||||||||||
резка за точкой B , а при λ (−1,0) |
– вне отрезка за точкой A. Переходя к |
|||||||||||||||
векторам, можно записать: |
|
|
|
|
|
|
||||||||||
AC |
= λ CB , что в координатном виде приводит к |
|||||||||||||||
равенствам x − x1 = λ(x2 − x) , y − y1 = λ( y2 − y), откуда можно найти координаты точки C :
x = |
x1 +λx2 |
, |
y = |
y1 +λy2 |
. |
(7.1) |
1+λ |
|
|||||
|
|
|
1+λ |
|
||
|
|
|
33 |
|
|
|
Если λ =1, то C является серединой отрезка AB и выражения (7.1) ста-
новятся формулами деления отрезка пополам: |
|
|
|
|
|
|
|||||||
|
x = |
x1 + x2 |
, |
y = |
y1 + y2 |
. |
|
|
|
(7.2) |
|||
|
|
|
|
||||||||||
|
|
2 |
|
|
|||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
||
Пример. В треугольнике ABC , где A(3,−7) , B(5,2) , C(−1,0) найдите |
|||||||||||||
длину медианы AD . |
|
|
|
|
|
|
|
|
|
|
|
|
|
По формулам (7.2) рассчитаем координаты точки D : |
|
|
|
|
|
|
|||||||
x = 5 −1 = 2 , |
|
y = 2 +0 =1. |
|
|
|
|
|
|
|
|
|
||
2 |
2 |
|
|
|
|
|
|
|
|
|
|
||
Отсюда, по формуле расстояния между точками: |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
AD = |
(2 −3)2 +(1+7)2 |
= |
|
. |
|
|
||||
|
|
|
65 |
|
|
||||||||
|
|
|
|
В пространстве декартова прямо- |
|||||||||
|
|
|
угольная система координат вводится |
||||||||||
|
|
|
аналогично. В качестве базиса выбирают |
||||||||||
|
|
|
три взаимно перпендикулярных единич- |
||||||||||
|
|
|
ных вектора i , j , k , исходящих из об- |
||||||||||
|
|
|
щей точки O (начала координат). Через |
||||||||||
|
|
|
начало координат проводят оси, направ- |
||||||||||
|
|
|
ленные так же, как векторы |
i , j , k – |
|||||||||
это ось абсцисс Ox , ось ординат Oy |
и ось аппликат Oz |
соответственно |
|||||||||||
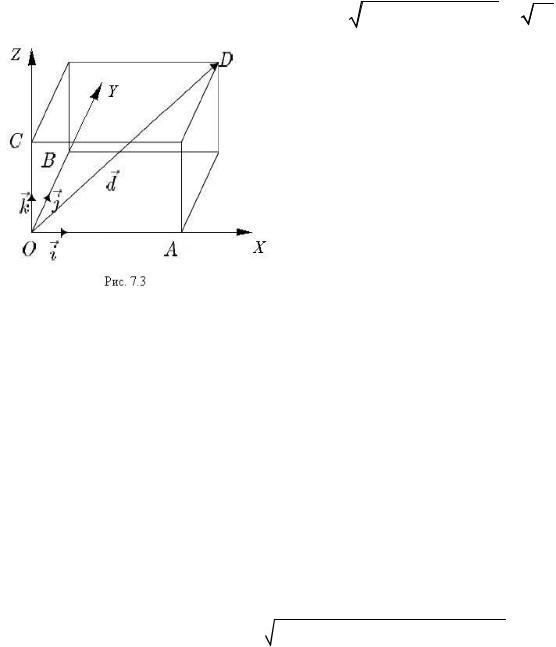
(рис. 7.3). Координаты точки D(x, y, z) |
равны координатам радиус-вектора |
||||||||||||
OD этой точки: OD = OA +OB +OC = xi + y j + zk . |
|
|
|
|
|
|
|||||||
Если ϕ1 , ϕ2 , ϕ3 |
– углы наклона вектора OD = d к осям, |
|
то x = d cosϕ1 , |
||||||||||
y = d cosϕ2 , z = d cosϕ3 . Числа cosϕ1 , |
cosϕ2 , cosϕ3 называются направ- |
||||||||||||
ляющими косинусами вектора d . Очевидно, что cos2 ϕ +cos2 ϕ |
2 |
+cos2 ϕ |
3 |
=1. |
|||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|||
Для двух точек с известными координатами M1(x1, y1, z1) и M2 (x2 , y2 , z2 )
можно найти координаты соединяющего их вектора M1M2 ={x2 −x1, y2 − y1,z2 −z1},
расстояние между ними M1M2 = 
 (x2 − x1)2 +( y2 − y1)2 +(z2 − z1)2 , координаты
(x2 − x1)2 +( y2 − y1)2 +(z2 − z1)2 , координаты
34
точки M (x, y, z) , делящей отрезок M1M2 в известном отношении λ = M1M : |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
MM2 |
x = |
x1 +λx2 |
, y = |
|
y1 +λy2 |
, |
z = |
z1 +λz2 |
. |
|
|
|||
1+λ |
|
|
|
|
|||||||||
|
|
|
|
1+λ |
|
1+λ |
|
|
|||||
|
|
|
В заключение лекции рассмотрим правила |
||||||||||
|
|
преобразования координат точки (вектора) при |
|||||||||||
|
|
параллельном переносе и повороте системы. |
|||||||||||
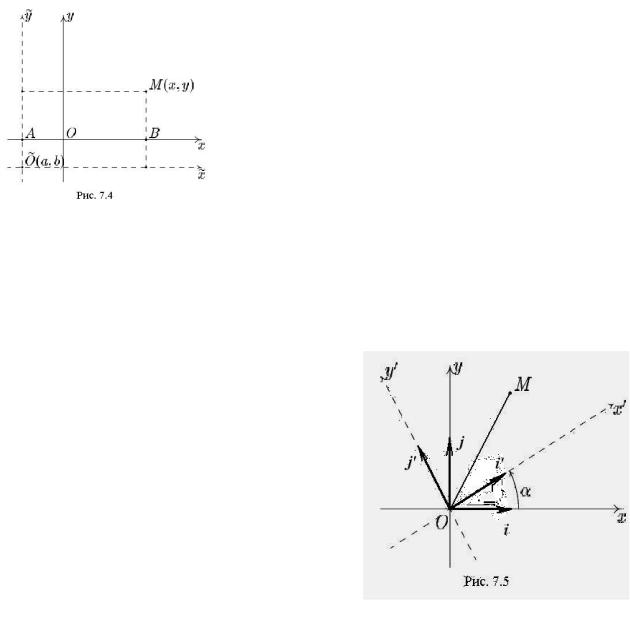
|
|
|
При параллельном переносе (на рис. 7.4 по- |
||||||||||
|
|
казан плоский случай) новое начало имеет в |
|||||||||||
|
|
старом |
|
|
базисе |
координаты |
O(a,b). Но |
||||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||||
|
|
OM |
=OO |
+ OM , |
или OM |
= −OO + OM |
, что в |
||||||
координатной записи имеет вид |
x = −a + x , |
y = −b + y . Здесь x и y |
– коор- |
||||||||||
динаты точки M в новом базисе. |
Обобщение на пространственный случай |
||||||||||||
очевидно. Итак, если система, полученная из первоначальной параллельным
переносом, |
имеет начало в точке O(a,b,c), |
|
|
|
|
|
|
|
|
||||||
то связь между старыми (x, y, z) |
и новыми |
|
|
|
|
|
|
|
|
||||||
(x, y, z) координатами |
точки |
M |
дается |
|
|
|
|
|
|
|
|
||||
формулами |
x = x + a , y = y + b , |
z = z + c . |
|
|
|
|
|
|
|
|
|||||
|
Далее, пусть дана система координат |
|
|
|
|
|
|
|
|
||||||
Oxy и полученная из нее поворотом на угол |
|
|
|
|
|
|
|
|
|||||||
α |
относительно точки |
O |
|
|
′ ′ |
|
|
|
|
|
|
|
|
||
система Ox y |
|
|
|
|
|
|
|
|
|||||||
(рис. 7.5). Разложим базисные векторы по- |
|
|
|
|
|
|
|
|
|||||||
вернутой |
системы |
по |
старому |
базису: |
|
|
|
|
′ ′ |
|
′ ′ |
|
|||
′ |
|
|
′ |
|
|
|
|
|
|
|
|
+ y |
. |
||
i |
= cosα i +sinα j , |
j |
= −sinα i |
+cosα j . |
Но OM |
= xi |
+ y j |
= x i |
j |
||||||
Подставив |
выражения |
i′, |
j′ |
через i , |
j , |
получим: |
|
|
|
|
|
||||
|
xi + y j = x′ (cosα i +sinα j) + y′ (−sinα i +cosα j) . |
|
|
|
|
||||||||||
Приравнивая коэффициенты при i и j в правой и левой частях последнего равенства, получим выражения старых координат через новые:
35

x = x′cosα − y′sinα , y = x′sinα + y′cosα . Выражение новых координат
через старые получается, очевидно, из последних |
формул заменой |
α → (−α) : x′ = x cosα + y sinα , y′ = −xsinα + y cosα . |
Поворот системы в |
пространственном случае выходит за рамки нашего курса. |
|
Лекция 8
Определение. |
Скалярным произведением векторов a и b называется |
|
число (a,b) , равное произведению модулей этих векторов |
||
на косинус угла |
между ними: (a,b) =| a | | b | cosϕ , |
где |
ϕ = (a,b) – угол между векторами a и b (рис. 8.1). |
|
|
Величину | b | cosϕ назовем проекцией вектора b |
на |
|
направление вектора a и обозначим прa b. Таким образом можно записать:
(a,b) =| a| прa b =|b| прb a . Скалярное произведение |
обладает следующими |
свойствами: 1) (a,b) = (b,a) (коммутативность); 2) |
(a,b +c) = (a,b) +(a,c) |
(дистрибутивность); 3) (λa,b) = λ(a,b), λ (однородность).
Свойства 1) и 3) очевидны из определения, а дистрибутивность доказывается следующим образом:
(a,b +c) =| a| прa (b +c) =|a| (прa b +прa c) =|a| прa b+ |a| прa c = (a,b)+(a,c).
Здесь мы воспользовались тем, что проекция суммы векторов равна сумме их проекций.
Пусть векторы a и b заданы в декартовой прямоугольной системе коор-
динат: a = (α1,α2 ,α3 ) ,b = (β1,β2 ,β3 ). Тогда (a,b) = (α1i +α2 j +α3k, β1i +β2 j +β3k) =
= α1β1(i,i) +α2β2 ( j, j) +α3β3 (k,k) = α1β1 +α2β2 +α3β3 , поскольку
(i, j) = (i,k) = ( j,k) = 0 в силу взаимной перпендикулярности базисных векто-
|
|
|
|
|
|
|
|
ров i, j,k . Ясно также, что (a,a) =| a |2 =α |
2 +α |
2 +α 2 |
| a |= |
α |
2 +α |
2 +α 2 . |
|
1 |
2 |
3 |
|
1 |
2 |
3 |
|
Сопоставляя определение скалярного произведения и его выражение в декар-
товой системе, получим формулу для угла между векторами:
36
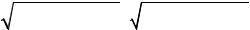
ϕ = arccos |
|
|
α1β1 +α2β2 +α3β3 |
|
|
. |
(8.1) |
||||
|
|
|
|
|
|
|
|
|
|||
α 2 |
+α |
2 +α 2 |
|
β |
2 + β 2 |
+ β 2 |
|||||
1 |
2 |
3 |
|
1 |
2 |
3 |
|
|
|
||
Заметим, что формула (8.1) дает ϕ [0,π], что соответствует интервалу изменения угла между геометрическими векторами.
Утверждение. Для того чтобы два вектора были ортогональны (т.е. перпендикулярны), необходимо и достаточно, чтобы их скалярное произведение равнялось нулю. Этот критерий ортогональности векторов очевиден из оп-
ределения скалярного произведения.
Определение. Упорядоченная тройка некомпланарных векторов называется правой, если составляющие ее векторы, будучи приведены к общему началу, располагаются в порядке нумерации аналогично тому, как расположены большой, указательный и средний пальцы правой руки.
Например, так расположены базисные векторы i, j,k определенной в лекции 7 декартовой прямоугольной системы координат, поэтому ее называ-
ют правой системой.
Определение. Упорядоченная тройка некомпланарных векторов называется левой, если составляющие ее векторы, будучи приведены к общему началу, располагаются в порядке нумерации аналогично тому, как расположены большой, указательный и средний пальцы левой руки.
Левую тройку можно получить из правой, если переставить два соседних вектора тройки или поменять направление любого вектора тройки на противоположное. Напротив, при циклической перестановке, т.е. при переходе от тройки a,b,c к тройкам b,c,a и c,a,b ориентация тройки (ее свойство быть правой или левой) не меняется. Тройки компланарных векторов не относятся ни к правым, ни к левым.
Определение. Векторным произведением векторов a и |
b называется |
||
вектор c , обозначаемый |
c =[a,b] (или |
a ×b), который |
определяется |
следующими тремя условиями:
37
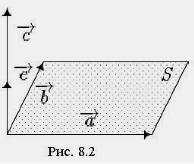
1) длина |
вектора c равна | c |=| a | | b | sinϕ , |
|
|
|
– угол между векторами a и b; |
где ϕ = (a,b) |
2)c a , c b ;
3)тройка a,b,c является правой (рис. 8.2).
Перечислим свойства векторного произведения: |
|
1) [a,b] = −[b,a] (антикоммутативность); 2) [a,b +c] =[a,b]+[a,c] |
(ди- |
стрибутивность); 3) [λa,b] = λ[a,b], λ (однородность). Свойства 1) и 3) |
|
очевидны; доказательство дистрибутивности остается за рамками курса. |
Из |
антикоммутативности, в частности, следует, что [a,a] = 0 , а также т.н. |
кри- |
терий коллинеарности векторов:
Утверждение. Для того чтобы два вектора были коллинеарны, необходимо и достаточно, чтобы их векторное произведение было равно нулю.
Теорема (геометрический смысл векторного произведения). Длина векторного произведения численно равна площади параллелограмма, построенного на векторах-сомножителях как на сторонах.
Доказательство. Из рисунка 8.2 и пункта 1) определения видно, что c =[a,b] = S e , где S — площадь параллелограмма со сторонами a и b, а
e – единичный вектор, перпендикулярный a и b и образующий с ними правую тройку. Тогда |[a,b]|= S .
Пусть i, j,k — базис правой декартовой прямоугольной системы координат. Пользуясь только определением векторного произведения, легко установить, что [i,i] =[ j, j] =[k,k] = 0, [i, j] = k , [ j,k] = i , [k,i] = j . Учитывая это,
вычислим векторное произведение [a,b] через координаты сомножителей a = (α1,α2 ,α3 ) и b = (β1, β2 , β3 ) в правой декартовой системе. Получим:
[α1i +α2 j +α3 k, β1i + β2 j + β3 k] = (α2β3 −α3β2 )i −(α1β3 −α3β1) j +(α1β2 −α2β1)k ,
или в символической записи
38
|
i |
j |
k |
|
|
[a,b] = |
α1 |
α2 |
α3 |
. |
(8.2) |
|
β1 |
β2 |
β3 |
|
|
Определение. Смешанным произведением трех векторов a,b,c назы-
вается скалярное произведение векторного произведения [a,b] и вектора c ,
т.е. число ([a,b],c).
Теорема (геометрический смысл смешанного произведения). Сме-
шанное произведение ([a,b],c)равно объему параллелепипеда, построенного на векторах-сомножителях как на ребрах, взятому со знаком «+», если тройка a,b,c правая и со знаком «−», если эта тройка левая.
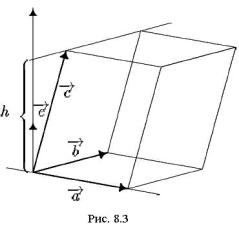
Доказательство. Пусть векторы a , b, c
некомпланарны и пусть S – площадь параллелограмма, построенного на векторах a , b. Если e – орт векторного произведения, то
([a,b],c) = S(e,c) = S пр c (рис. 8.3). Оче- |
|
|
e |
видно, пр c = ±h , где |
h – высота параллеле- |
e |
|
пипеда, построенного на приведенных к общему началу векторах a , b, c , причем знак
выбирается в зависимости от ориентации тройки. Значит, ([a,b],c)= ±V , где V – объем параллелепипеда.
Следствием теоремы является т. н. критерий компланарности векторов: Утверждение. Для того чтобы три вектора были компланарны, необходимо и достаточно, чтобы их смешанное произведение было равно нулю.
(Тогда V = 0 ). |
|
Пусть в |
правой декартовой системе координат заданы векторы |
a = (α1,α2 ,α3 ) , |
b = (β1, β2 , β3 ) , c = (γ1,γ2 ,γ3 ) . Тогда их смешанное произведе- |
ние вычисляется по формуле
39
