
линейная алгебра и агалитич геом
.pdfОпределение. Ранг матрицы A (обозначается rang A) – это число, равное наибольшему порядку отличного от нуля минора этой матрицы, т.е. rang A = r , если все миноры порядка большего, чем r (если они существуют),
равны нулю, а среди миноров порядка r есть хотя бы один отличный от нуля. Данное определение дает способ вычисления rang A.
Теорема. При элементарных преобразованиях ранг матрицы не меняется. Чтобы вычислить ранг матрицы A, можно поступить следующим образом.
Приведем матрицу к ступенчатому виду элементарными преобразованиями над строками (см. пример на метод Гаусса в лекции 3). Число ненулевых строк ступенчатой матрицы будет равно рангу матрицы A.
|
0 |
2 |
−4 |
|
Пример. Вычислим ранг матрицы A = −1 |
−4 |
5 |
. |
|
|
3 |
1 |
7 |
|
|
0 |
5 |
−10 |
|
Вначале приведем матрицу к ступенчатому виду. Покажем последова-
−1 −4 |
5 |
|
−1 −4 |
5 |
|
−1 |
−4 5 |
|||||||
|
0 |
−11 |
22 |
|
|
0 |
2 |
−4 |
|
|
0 |
2 |
4 |
|
тельность выкладок: A |
|
|
|
|
. |
|||||||||
|
0 |
2 |
−4 |
|
|
0 |
−11 |
22 |
|
|
0 |
0 |
0 |
|
|
0 |
5 |
−10 |
|
|
0 |
5 |
−10 |
|
|
0 |
0 |
0 |
|
|
|
|
|
|
|
|||||||||
Очевидно, что ранг последней матрицы равен 2, так как все миноры третьего порядка равны нулю (или число ненулевых строк равно 2). Следовательно, rang A = 2.
Пусть в некотором множестве W = {а, b, с,...} определена операция
сложения: |
αa + βb W , |
где a,b W ,α, β R . |
Определение. Элемент a множества W является линейной комбинацией |
||
элементов |
a1,...,am W , |
если существует m чисел α1,...,αm таких, что |
a =α1a1 +αmam. При этом говорят, что элемент a линейно выражается через элементы a1,...am .
20

Теорема Кронекера – Капелли. Пусть имеется система линейных уравнений (3.1). Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу ее расширенной матрицы: rang A = rang A.
Следствие. Пусть система (3.1) совместна. Решение системы единственное тогда и только тогда, когда rang А равен числу неизвестных (порядку) системы.
Укажем способ нахождения решения системы линейных уравнений. Пусть rang A = rang A = r < n и пусть, для определенности, базисный минор расположен в левом верхнем углу матрицы системы. Переменные x1, x2 ,...xr будем называть базисными переменными, xr+1, xr+2 ,..., xn – свободными. Далее, свободные переменные обозначим через c1,...,cn−r соответственно. Оставим только первые r уравнений системы (т. н. укороченная система). Из нее найдем x1, x2 ,...xr по формулам Крамера. В итоге получаем, что общее решение
системы будет иметь вид X = (x , x |
,..., x |
,c ,...,c |
|
)t . |
|
|||||||
|
|
|
|
1 |
2 |
r |
1 |
n−r |
|
|
|
|
Пример. Пусть расширенная матрица системы имеет вид |
||||||||||||
|
|
|
1 |
−2 |
0 |
1 |
| |
−3 |
|
|
||
|
|
= 3 |
−1 |
−2 |
0 |
| 1 |
|
. |
||||
|
A |
|||||||||||
|
|
|
2 |
1 |
|
−2 |
−1 |
| |
4 |
|
|
|
|
|
|
1 |
3 |
−2 |
−2 | 7 |
|
|||||
Приведем ее с помощью элементарных преобразований к ступенчатому виду:
|
1 |
−2 |
0 |
1 | −3 |
1 |
−2 |
0 |
1 |
| −3 |
|||||
|
|
0 |
5 |
−2 |
−3 |
| 10 |
|
|
0 |
5 |
−2 |
−3 |
| 10 |
|
|
|
|
|
. |
||||||||||
A |
||||||||||||||
|
|
0 |
5 |
−2 |
−3 |
| 10 |
|
|
0 |
0 |
0 |
0 |
| 0 |
|
|
|
0 |
5 |
−2 |
−3 |
| 10 |
|
|
0 |
0 |
0 |
0 |
| 0 |
|
|
|
|
|
|
||||||||||
Итак, что rang А = 2. Базисными будут переменные {x1, x2}, свободными
– {x3 |
, x4 |
}. Решаем укороченную систему: x1 − 2x2 = −3 − x4 , . В результате |
|
|
5x2 =10 + 2x3 + 3x4 |
|
|
21 |
|
|
x =1+ 4c / 5 +с / 5, |
||
|
|
1 |
1 |
2 |
получим |
x2 = 2 + 2c1 / 5 +3c2 / 5, |
|||
|
|
x3 = c1, |
|
|
|
|
|
|
|
|
|
|
x4 = c2 |
|
|
|
|
|
|
(общее решение системы, где c1 и c2 – произвольные числа.)
Однородные системы линейных уравнений.
Однородной называется система (3.1), в которой все bi = 0:
a |
x |
+a |
x |
2 |
+... +a |
|
x |
n |
|
= 0, |
|
|||||
|
11 |
1 |
|
12 |
|
|
1n |
|
|
|
|
|
||||
a21x1 |
+a22 x2 |
+... +a2n xn |
= 0, |
(4.1) |
||||||||||||
|
|
|
............................. |
|
|
|||||||||||
|
|
|
|
|
|
|||||||||||
a |
x |
+a |
m2 |
x |
2 |
+... +a |
mn |
x |
n |
= 0. |
|
|||||
|
m1 |
1 |
|
|
|
|
|
|
|
|
||||||
Более короткая |
запись |
|
|
|
системы |
|
|
(4.1) имеет вид AX = Θ, или |
||||||||
n
∑aij xj = 0,i =1,...,m .
j=1
Свойства решений однородной системы. 1) Пусть X и Y – решения системы, тогда Z =αX + βY – тоже решение системы, где α, β R .
Доказательство.
n |
n |
n |
|
n |
n |
|
∑aij (αxj + β y j ) = ∑aijαxj + |
∑aij β y j =α∑aij xj + β∑aij y j . |
|||||
j=1 |
j=1 |
j=1 |
|
j=1 |
j=1 |
|
2) По теореме Кронекера-Капелли однородная система всегда совместна. |
||||||
Доказательство. |
|
= (A | 0) rang |
|
= rang A, или, что более очевидно: |
||
A |
A |
|||||
тривиальное решение X = (0,...,0)t |
удовлетворяет |
нашей однородной систе- |
||||
ме линейных уравнений (4.1).
3) Если rang А = n, тогда тривиальное решение единственно. Доказательство. По условию rang A = n, следовательно, det A ≠ 0 . Поэтому мы можем найти решение Г = (γ1,...,γn )t системы по форму-
лам Крамера (3.3), (3.4), т.е. di = 0,i =1,...,n . Следовательно, все γi = 0 .
4) Если rang A < n, то однородная система (4.1) имеет нетривиальное решение (при m = n это значит, что det A = 0).
22
Определение. Система элементов x1,..., xn называется линейно независимой, если из равенства α1x1 +... +αn xn =θ (здесь θ – нулевой элемент сис-
темы) следует, |
что все числа αi = 0 . Линейная комбинация с нулевыми ко- |
|||||||||||||
эффициентами называется тривиальной. |
|
|
|
|
|
|
|
|||||||
Определение. Система элементов называется линейно зависимой, если |
||||||||||||||
существуют числа αi , не все равные нулю, |
такие, что α1x1 +... +αn xn =θ . |
|||||||||||||
Пример. Выясним, являются ли данные три элемента (вектора) линейно |
||||||||||||||
|
|
|
|
0 |
|
|
|
|
3 |
|
|
|
3 |
|
независимыми. |
Пусть |
x |
= |
2 |
, x |
2 |
= |
|
0 |
, x |
3 |
= |
2 |
. Составим линейную |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
3 |
|
|
|
|
1 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
0 |
|
|
3 |
|
|
3 |
0 |
|
||||||||
комбинацию этих элементов α |
|
2 |
|
+α |
2 |
|
0 |
|
+α |
3 |
|
2 |
|
= |
0 |
|
. Последнее выра- |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
3 |
|
|
|
|
1 |
|
|
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
жение запишем в виде системы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3α2 +3α3 = 0, |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
0, |
|
|
|
|
|
|
|
|
|
(4.2) |
|
2α1 + 2α3 = |
|
|
|
|
|
|
|
|
|
||||||||
|
|
+α2 = 0. |
|
|
|
|
|
|
|
|
|
|
|
||||
3α1 |
|
|
|
|
|
|
|
|
|
|
|
||||||
Определитель этой однородной системы равен
|
|
0 |
3 |
3 |
|
2 |
2 |
|
2 |
0 |
|
= +18 +6 ≠ 0 . Следовательно, система (4.2) имеет |
|||||||||||
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||
|
|
2 |
0 |
2 |
= −3 |
+3 |
|
||||||||||||||||
|
|
3 |
1 |
0 |
|
3 |
0 |
|
3 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
только тривиальное решениеα1 =α2 =α3 = 0 , и, |
следовательно, система эле- |
||||||||||||||||||||||
ментов x1, x2 , x3 – линейно независима. |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
Пример. Выясним, являются ли данные три элемента (вектора) линейно |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
независимыми. |
Пусть |
|
|
|
|
0 |
|
X2 = |
|
0 |
|
X3 |
|
2 |
|
Составляем соотно- |
|||||||
|
X1 = |
, |
|
, |
= |
. |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
23
|
α |
+2α |
2 |
+3α |
3 |
= 0, |
|||
шение: α1 X1 +α2 X2 +α3 X3 |
|
1 |
|
|
|
|
|||
=θ , что приводит к системе |
|
2α3 = 0, |
|
||||||
|
|
α |
+2α |
2 |
+α |
3 |
= 0. |
||
|
|
1 |
|
|
|
|
|||
Определитель полученной однородной системы
|
1 |
2 |
3 |
|
1 |
2 |
|
= 0 . Значит, система элементов |
X1, X2 , X3 линейно за- |
|
|
|
|||||||
|
|
|
|||||||
|
0 |
0 |
2 |
= (−1)2 |
|
||||
|
1 |
2 |
1 |
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
висима. Укажем коэффициенты линейной комбинации αi ≠ 0 . Для этого приведем матрицу однородной системы к ступенчатому виду:
1 2 |
3 |
1 2 3 |
|
|
1 2 |
3 |
|
|||||||||
|
0 |
0 |
2 |
|
|
0 |
0 |
−2 |
|
|
|
0 |
0 |
−2 |
|
Последняя матрица определяет сис- |
|
|
|
|
|
. |
|||||||||||
|
1 |
2 |
1 |
|
|
0 |
0 |
2 |
|
|
|
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|||||||||
тему |
α1 +2α2 +3α3 = 0, |
Решая последнюю систему, получаем, что |
||||||||||||||
|
|
|
|
|
−2α3 = 0. |
|
|
|
|
|
|
|
|
|||
α1 = −2α2 ,α3 = 0 , где α2 можно задавать произвольно.
Лекция 5
Пусть имеется однородная система уравнений (4.1) и пусть rang A = r <n.
Определение. Фундаментальная система решений E1,..., En−r системы
(4.1) – это система линейно независимых решений, через которую можно выразить любое решение системы в виде их линейной комбинации.
Алгоритм нахождения E j :
(1) Находим rang A=r. Пусть r < n (в случае r = n решение тривиально), тогда будем иметь
a11x1 +... +a1r xr = −a1,r+1xr+1 +... |
||||||||||
a |
x +... +a |
2r |
x |
r |
= −a |
2,r+1 |
x |
r+1 |
+... |
|
|
21 1 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
....................................... |
|
|||||||||
|
|
+ +arr xr |
= −ar,r+1xr+1 + |
|||||||
ar1x1 |
||||||||||
|
|
|
|
24 |
|
|
|
|
||
Неизвестные x1, x2 ,...xr будем называть базисными, xr+1, xr+2 ,..., xn - свободными. (Здесь мы для удобства рассуждений считаем, что минор матрицы А стоящий на пересечении первых r строк и первых r столбцов, отличен от нуля.) Тогда решение однородной системы АХ = 0 имеет вид:
|
|
|
|
x1(c1,...,cn−r ) |
|
|
|||||
|
|
|
|
x |
(c ,...,c |
) |
|
|
|||
|
|
|
|
|
2 |
1 |
n−r |
|
|
|
|
|
|
|
|
|
|
........ |
|
|
|
|
|
|
|
X |
= |
x |
(c ,...,c |
) |
. |
|
(5.1) |
||
|
|
|
|
|
r |
1 |
n−r |
|
|
|
|
|
|
|
|
|
|
c1 |
|
|
|
|
|
|
|
|
|
|
|
....... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cn−r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Положим в (5.1) c1 =1, остальные ci |
= 0, получим E1 ; положим c2 =1, |
||||||||||
остальные ci = 0, получим Е2, |
и т.д. |
|
|
|
|
|
|||||
Пример. Пусть однородная система (4.1) задается матрицей: |
|
||||||||||
|
|
3 |
|
1 |
|
−8 |
2 |
|
1 |
|
|
|
|
2 |
−2 |
|
−3 |
−7 |
2 |
|
|
||
A = |
|
|
|
(5.2) |
|||||||
|
1 |
11 |
|
−12 |
34 |
|
−5 |
. |
|||
|
|
1 |
−5 |
|
2 |
−16 |
3 |
|
|
||
|
|
|
|
|
|||||||
Найдем фундаментальную систему решений данной однородной системы. Проверьте, что все миноры третьего порядка равны нулю, т. е. rang A = 2 .
Теперь рассмотрим укороченную систему
3x + x |
|
=8x −2x |
|
− x , |
(5.3) |
|
|
1 |
2 |
3 |
4 |
5 |
|
2x1 −2x2 = 3x3 +7x4 −2x5. |
|
|||||
Переменные {x1, x2} – |
базисные, |
|
{x3, x4 , x5} |
– свободные. Положим |
||
x3 = c1, x4 = c2 , x5 = c3 .
Решаем укороченную систему (5.3) по формулам Крамера:
d = |
|
3 |
1 |
|
= −8,d1 = |
|
8c1 −2c2 −c3 |
1 |
|
,d2 = |
|
3 |
8c1 −2c2 −c3 |
|
. |
|
|
|
|
|
|
||||||||||
|
|
2 |
−2 |
|
|
|
3c1 +7c2 −2c3 |
−2 |
|
|
|
2 |
3c1 +7c2 −2c3 |
|
|
Отсюда решение укороченной системы имеет вид:
x1 = d1 / d = −(1/ 8)(−19c1 −3c2 +4c3 ) , x2 = d2 / d = −(1/ 8)(−7c1 +25c2 −4c3 ) .
25
|
Построим фундаментальную систему решений нашей однородной сис- |
||||||
темы. Для этого положим |
c1 =1,c2 |
= c3 = 0 и найдем E1 . |
Далее, положим |
||||
c2 |
= c3 = 0,c2 =1 и получим E2 ; положим c1 = c2 = 0, c3 =1, |
чтобы найти E3 . |
|||||
В итоге имеем: |
|
|
|
|
|
|
|
E |
= (19 / 8;7 / 8;1;0;0)t , E |
2 |
= (3 / 8; |
−25 / 8;0;1;0)t , E |
3 |
= (−1 / 2;1 / 2;0;0;1)t . |
|
1 |
|
|
|
|
|
||
Тогда общее решение однородной системы имеет вид
Xодн. =α1E1 +α2 E2 +α3E3,αi R .
Нахождение общего решения системы АХ = В.
Пример. Пусть система линейных уравнений определяется расширен-
|
|
|
|
2 |
1 |
−1 |
−3 |
| |
2 |
|
|
ной матрицей |
|
|
= 4 |
0 |
1 |
|
−7 |
| |
3 |
. |
|
|
A |
||||||||||
|
|
|
|
0 |
2 |
−3 |
1 |
| |
1 |
|
|
|
|
|
|
2 |
2 |
−4 |
−2 |
| 3 |
|||
Убеждаемся, что |
rang A = rang |
|
и, |
следовательно, исходная система |
|||||||
A |
|||||||||||
совместна. Так как rang А = 2, то число базисных неизвестных равно 2; n −r = 2 – число свободных неизвестных. Разыскиваем минор второго поряд-
ка, отличный от нуля. Берем M2(1) |
= |
|
2 1 |
|
, (в качестве базисного можно так- |
||||||||
|
|
||||||||||||
|
|
|
|
|
|
|
|
4 |
0 |
|
|
|
|
же выбрать минор M2(2) = |
|
2 |
−3 |
|
|
или другой минор второго порядка, отлич- |
|||||||
|
|
||||||||||||
|
|
2 |
−2 |
|
|
|
|
|
|
|
|
|
|
ный от нуля.) Базисный минор M2(1) |
|
мы выбираем из соображений удобства. |
|||||||||||
Тогда x1, x2 – базисные переменные, |
|
x3, x4 – свободные переменные. В итоге |
|||||||||||
имеем укороченную систему |
2x1 + x2 |
= 2 + x3 +3x4 , 4x1 = 3− x3 +7x4 . |
|||||||||||
Решая укороченную систему, получаем общее решение: |
|||||||||||||
|
|
|
3/ 4 −1/ 4c1 +7 / 4c2 |
|
|||||||||
X |
|
|
1/ 2 +3/ 2c −1/ 2c |
|
|||||||||
общ. |
= |
|
|
|
1 |
2 |
. |
||||||
|
|
|
|
|
c |
|
|
||||||
|
|
|
|
|
|
|
1 |
|
|
||||
|
|
|
|
|
|
c2 |
|
||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
26 |
|
|
|
|
||
В данном примере нетрудно выписать общее решение однородной системы
|
|
−1/ 4c |
+7 / 4c |
|
|||
соответствующей данной неоднородной: X |
|
|
3 / 2c 1− |
1/ 2c |
2 |
|
|
одн. |
= |
1 |
c |
2 |
|
. |
|
|
|
|
|
|
|
||
|
|
|
|
1 |
|
|
|
|
|
|
c2 |
|
|
||
|
|
|
|
|
|
|
|
Из последней формулы легко находим систему фундаментальных решений однородной системы:
E = (−1 / 4,3 / 2,1,0)t , E |
2 |
= (7 / 4, −1 / 2,0,1)t . |
|
1 |
|
|
|
Тогда Xодн. =α1E1 +α2 E2 ,α1,α2 R . Частное решение неоднородной |
|||
системы получим из |
общего, положив здесь c1 =1,c2 =1, исходя из сооб- |
||
ражений удобства. Xч.неодн. = (9 / 4,3 / 2,1,1)t . Тогда общее решение исходной системы можно записать в виде: Xобщ. = Xодн. + Xч.неодн.
Вывод: Если задана неоднородная система АХ = В, то общее решение
Xобщ. = Xодн. + Xч.неодн. , так как A(Xодн. + Xч.неодн. ) = AXч.неодн. = B .
Раздел III. Векторная алгебра
Лекция 6
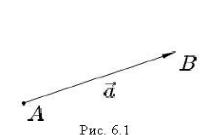
Векторы – это такие величины, которые имеют не только численное значение, но и определенное направление. Многие физические величины являются векторами: например, сила, перемещение, скорость, ускорение.
Определение. |
Геометрическим |
вектором, |
или просто вектором, называется направленный |
||
отрезок (рис. 6.1). |
|
|
Будем обозначать вектор символом |
AB или a , а его длину | AB | или |
|
| a |, где A и B обозначают начало и конец данного направленного отрезка. Начало вектора называют точкой приложения этого вектора. Точка приложения геометрического вектора может быть выбрана произвольно, т.е. два
27
вектора, полученные один из другого параллельным переносом, считаются равными. Вектор θ называется нулевым, если его начало и конец совпадают. Нулевой вектор не имеет направления. Векторы a и b называются коллинеарными (обозначается a b ), если они лежат либо на одной, либо на параллельных прямых. Нулевой вектор коллинеарен любому вектору.
Теперь можно сформулировать понятие равенства двух векторов: два вектора называются равными, если они коллинеарны, имеют одинаковую длину и одинаковое направление.
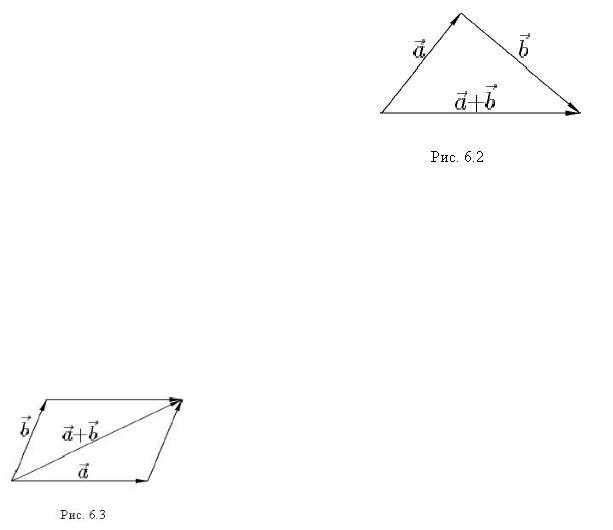
Определение. Суммой a +b двух векторов a и b называется вектор, исходящий из начала вектора a в конец
вектора b при условии, что вектор b приложен к концу вектора a (рис. 6.2).
Это так называемое правило треугольника сложения векторов. Операция сложения двух векторов подчиняется закону коммутативности a +b = b +a и ас-
социативности (a +b) +c = a +(b +c) . Для каждого вектора a справедливо равенство a +θ = a . Кроме того, нетрудно проверить, что для a (−a) та-
кой, что a +(−a) =θ . Вектор (−a) называется вектором, противоположным
вектору a .
Коммутативный закон сложения векторов имеет геометрическую интерпретацию, извест-
ную как правило параллелограмма: если a и b
приложены к общему началу и на них как на сторонах построен параллелограмм, то сумма этих векторов представляет собой диагональ паралле-
лограмма, исходящую из общего начала векторов a и b (рис. 6.3).
28
Свойства операции сложения позволяют распространить правило сложения на сумму любого конечного числа векторов.
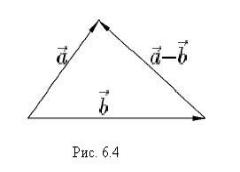
Определение. Разностью векторов a −b называется такой вектор, который в сумме с вектором b дает вектор a . (Обратите внимание на то, что операция вычитания векторов определяется через уже введенную операцию сложения.)
С |
помощью |
свойств |
операции сложения |
нетрудно |
показать, что |
c = a +(−b), где |
(−b) – |
вектор, противоположный b. |
Действительно, |
||
c +b = (a +(−b))+b = a +((−b) +b)= a +θ = a , т.е., |
согласно определению, |
||||
вектор |
c представляет собой разность a −b. |
|
|
||
Из определения разности и правила треуголь- |
|
|
|||
ника сложения векторов вытекает правило по- |
|
|
|||
строения разности: разность двух приведенных к |
|
|
|||
общему началу векторов представляет собой век- |
|
|
|||
тор, идущий из конца вычитаемого вектора в к о- |
|
|
|||
нец уменьшаемого (рис. 6.4). |
|
|
|||
Определение. |
Произведением αa вектора a на действительное число |
||||
α называется вектор b такой, что 1) a b ; 2) | b | =|α | | a |; |
3) b направлен |
||||
так же, как вектор a , в случае α > 0 и противоположно направлен в случае
α < 0.
Основные свойства введенной операции таковы: 1) α(a +b) =αa +αb ;
2) (α + β)a =αa + βb (дистрибутивность); 3) (αβ)a =α(βa) (ассоциатиность). Эти свойства очевидны из наглядных геометрических соображений.
Определение. Линейной комбинацией векторов a1,a2 ,...,an называется
выражение вида α1a1 +α2 a2 +... +αn an , αi i =1,...,n . Числа αi называются коэффициентами линейной комбинации. Линейная комбинация называ-
29
