лекции вышмат

Добавил:

VadoZ хачю сдать сессию Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский технический университет связи и информатики

Предмет:

Высшая математика

Файл:

Теперь, дифференцируя

= S ( x) =

.pdf

Скачиваний:

Добавлен:

01.06.2024

Размер:

5.41 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 1920 / 2520 21 22 23 24 25 > Следующая >>>

Теорема 3. Сумма степенного ряда непрерывна на интервале (−R, R) .

Теорема 4. Степенной ряд с радиусом сходимости R можно почленно дифференцировать и интегрировать от 0 до x сколько угодно раз внутри интеграла сходимости. При этом радиусы сходимости всех получаемых степенных рядов будут равны радиусу сходимости исходного ряда R .

Доказательство теорем 3 и 4 требует рассмотрения достаточно сложного понятия равномерной сходимости функциональных и степенных рядов, и для экономии места и времени мы его здесь приводить не будем.

Примеры. Найти сумму степенного ряда при помощи почленного интегрирования и дифференцирования.

1. nxn −1 = S ( x) .

n =1

Решение. По формуле (4), в которой

–

коэффициент при

– равен

n +1 , имеем:

R = lim

n + 1

= 1

; при

| x | 1

n →

n + 2

проинтегрируем почленно:

S ( x)dx = n x

n −1

= n

= x

(в последнем переходе использовалась формула суммы бесконечно

1 − x

n =1

убывающей геометрической прогрессии с первым членом

и знаменателем

x ).

обе части полученного равенства по

x	)	/	1 − x + x			1
		=			=			, т.е.	S (
1 − x			(1 − x)	2		(1 − x)	2

x x)

, имеем

=	1
		2
	(1 − x)

(−1,1)

			(−1)
2.			n(n −
	n =	2	n(n −

Решение. R

S ( x) =

n =2

n
x	n	= S ( x) .
x		= S ( x) .
1)
= lim			(n + 1)n	=
= lim			n(n − 1)	=
n →			n(n − 1)
(−1)		n	n xn −1 =


n(n −1)				n =2

; при

(−1)n

(n −1)

| x |

xn −1 ,

1	дифференцируем два раза почленно:
		(−1)n (n −1)		1
S ''(x) =			xn − 2 = (−1)n xn − 2 =		.
S ''(x) =			xn − 2 = (−1)n xn − 2 =		.
	n =2	(n −1)	n =2	1 + x

(в последнем переходе использовалась формула суммы бесконечно убывающей геометрической прогрессии с первым членом 1 и знаменателем −x ).

Теперь два раза интегрируем обе части полученного равенства от 0 до x

( | x | 1 ):

= S '(x)

= ln(1 + x) (из формулы выше видно, что

S '(0) = 0 );

S ''( x)dx = S '(x)

1 + x

= ln(1 + x)

1 − 1

dx =

S '( x)dx = S ( x)|0

= S (x) = ln(1 + x)dx = x ln(1 + x)|0

−

x dx = x ln(1 + x) −

(

)

x + 1

1 + x

= x ln(1 + x) − x + ln(1 + x)|

= x ln(1 + x) − x + ln(1 + x)

(из формулы выше видно, что S(0) = 0 ), т.е.

S(x) = x ln(1 + x) − x + ln(1 + x) ,

x (−1,1) .

Пусть теперь дан ряд

an (x − x0 )n . Как уже отмечалось,

после замены

n=0

x − x	0	= t
	0

он

превращается в обычный степенной ряд an t n , для которого справедливы все полученные

n=0

190

выше результаты. Значит, ряд

R −	радиус сходимости ряда


an (x −
n=0

an t	n	),
an t		),
n=0

x		)	n
	0

т.е.

сходится абсолютно при |

при

− R x −x0 R , или

t |=| x − x0

− R x

(где

R , и

расходится при

\| t \|=\| x − x	0

, т.е. при

x x	0	− R
	0

. Этот ряд можно почленно

дифференцировать и интегрировать от

x	0

до

(при

x = x	0	+t
	0

t ...

	x	+t		x
	0			x
dt =			... dx = ...
	x	0		x	0
		0			0

)

сколько угодно раз с сохранением области сходимости.

Разложение функций в степенные ряды.

В этом параграфе будет изучаться возможность разложения функции в степенной ряд, т.е. представления ее в виде суммы степенного ряда. Пусть такое представление возможно:

f (x) = an (x − x0 )n ,

n=0

\| x − x	0	\| R
	0

(6)

Используя возможность почленного продифференцируем обе части равенства (6)

дифференцирования	степенного	ряда,
k раз, k =1,2,...Учитывая, что производная

постоянной равна 0, получим:


f '(x) = an n(x − x0 )n−1					,	f ''(x) = an n(n −1)(x − x0 )n−2 , …,
		n=1				n=2

f	(k )	(x) =	an n(n −1)	... (n − k +1)(x − x0 )			n−k	, \| x − x0	\| R .
f		(x) =	an n(n −1)	... (n − k +1)(x − x0 )				, \| x − x0	\| R .
			n=k

(7)

Положим в формуле (7)

x =

x	0

Тогда все слагаемые в правой части, кроме первого (

n = k

обратятся в 0, и мы получим	f	(k )	(x0

Таким образом, если разложение определяются по формулам

)

= a	k
	k
(6)

		f	(
k!; ak	=

возможно,

k )
(x	0
	0
k!

то

)	.

его коэффициенты обязательно

		f	(n)	(x		)
an	=	f		(x	0	)	, n = 1,2,…
					0
			n!
			n!

Т.е. разложение функции в степенной ряд единственно и имеет вид

(8)

f(x) =

n=0

f	(n)	(x		)
f		(x	0	)	(x −
					(x −

	n!

x		)	n
	0

(9)

Ряд в правой части этой формулы называется рядом Тейлора для функции					f (x) . В
частности, при x0 = 0
		(n)
f (x) =	f		(0)	xn .	(10)

n=0		n!

Однако примеры показывают, что наличие у функции всех производных и сходимость ее ряда Тейлора еще не являются достаточными условиями справедливости разложения (9).

Теорема 5. Пусть функция y = f (x) имеет в некоторой окрестности U (x0 ) производные любого порядка. Тогда для справедливости разложения (9) в этой окрестности необходимо

и достаточно, чтобы для x U (x )	lim r (x) = 0	, где	r (x) =	f (n+1) (c)	(x − x		)n+1	−

0	n→ n		n	(n +1)!		0

191

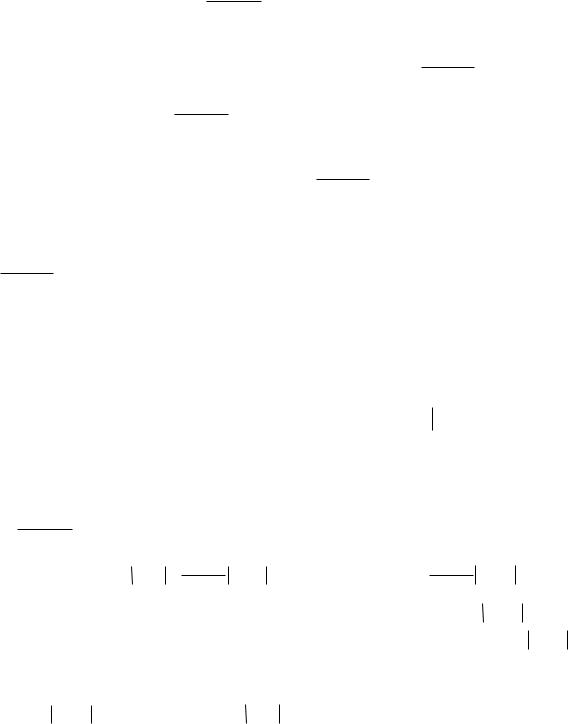
остаточный член формулы Тейлора в форме Лагранжа ( c −

промежуточная точка между

и x ).

▲ Разложим функцию y = f (x)

по формуле Тейлора в окрестности

U (x0 ) :

(k )

)

f (x) =

− x0 )

+ rn

(x)

(11)

k =0

и перейдем в этой формуле к пределу при

n → .

(k )

(x )

(x) −

Пусть справедлива формула (9). Тогда из (11) rn (x) = f

(x − x0 )

k !

k =0

f (k ) (x

)

f (k ) (x )

(x − x )k

(9)

lim r

(x) = lim f

(x) − lim

(x − x

)

= f (x) −

= 0 .

n→

k !

k =0

(k )

(x )

Пусть, наоборот,

lim rn (x) = 0 . Тогда из (11)

(x − x0 )

= f (x)

− rn (x)

k !

n→

k =0

(k )

(x0 )

lim

(x − x0 )k = lim f (x) − lim rn (x) = f (x) −0 = f (x) , значит,

n→ k =0

n→

(k )

)

(x − x0 )

= f (x) , т.е. справедлива формула (9). ■

k !

k =0

Проверка выполнения условия lim rn (x) = 0

на практике затруднительна, поэтому приведем

n→

следующее достаточное условие возможности разложения функции в ряд Тейлора.

Теорема 6. Пусть функция y = f (x) имеет любого порядка. Пусть M 0 : x U (x0x U (x0 ) справедливо разложение (9).

в некоторой окрестности

) , n = 0, 1, 2,… ( f (n)

U (x	0

(x)

)

производные ). Тогда для

▲ Согласно теореме

	f	(n+1)	(c)
= lim	f		(c)	(x − x	)	n+1
						n+1

n→	(n +1)!			0
n→	(n +1)!

5,	нам достаточно доказать, что для x U (x0 )
= 0	, c между x0 и x .

lim r		(x) =
n→	n
n→

n+1

По условию теоремы rn (x)

x − x0

. Рассмотрим ряд

x − x0

. Этот ряд

(n +1)!

n=0

(n +1)!

сходится

по

признаку

Даламбера,

так

как

lim

M x − x0 n+2 (n +1)!

n+1

n→ (n + 2)!M x − x

= lim

| x − x0 |

= 0 1.

Отсюда, в

силу

необходимого

признака

сходимости ряда,

n + 2

n→

lim

x − x

n+1 = 0 . Но тогда и lim r (x) = 0

. ■

n→ (n +1)!

n→ n

Примеры разложений функций в ряд Тейлора при x0 = 0 .

1. f (x) = e x .

f (n) (x) = e x , f (n) (0) =1, n = 0, 1,

2,...

192

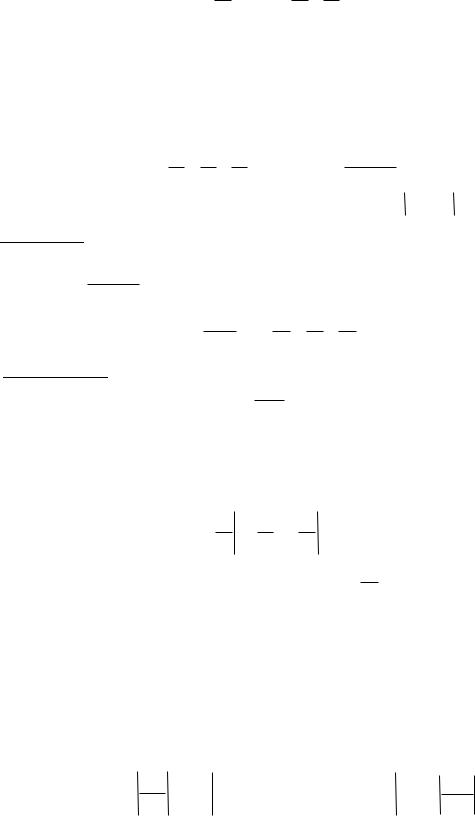
+ x +

+... .

(12)

n=0

Из теоремы 6 следует, что разложение справедливо на любом отрезке − H , H , так как на

этом отрезке

f (n) (x)

eH ,

n = 0

,1, 2,... , значит,

это разложение справедливо на всей

прямой.

2. f (x) = sin x

. f (0) = 0, f '(x) = cos x ,

'(0) =1,

f "(x) = −sin x ,

f "(0) = 0 ,

f '''(x) = −cos x ,

f '''(0) = −1, f

(x) = sin x,

…

2n+1

sin x = x −

−

+... = (−1)

(13)

(2n +

1)!

n=0

Разложение справедливо на всей прямой, так как для всех

(n)

(x) 1,

n = 0, 1, 2,...

3.	f (x) = cos x . Продифференцируем обе части полученного разложения (13) (степенной

ряд

cos

правой его части

можно

дифференцировать почленно

по всей

прямой):

2n +1

(−1)

(2n

+1)!

n=0

cos x = (−1)

=1−

−

+...

(14)

n=0

(2n)!

) = ln(1+ x) .

Проверка

выполнения

условий теоремы 6 здесь

довольно

сложна,

поэтому поступим по-другому:	f '(x) =	1	.

	1	+ x

Правая часть этой формулы является суммой бесконечно убывающей геометрической


прогрессии с первым членом	b1		=1		и знаменателем q = −x , следовательно, при \| q \| 1, т.е.
при x (−1, 1) f '(x) =1− x + x		2	− x	3	+... (пишем саму прогрессию). Интегрируем обе части
при x (−1, 1) f '(x) =1− x + x			− x		+... (пишем саму прогрессию). Интегрируем обе части

этого равенства от 0 до

(степенной ряд в правой части интегрируем почленно):

f '(x)dx = f (x)|

= ln(1+ x) = x|

−

+... , т.е.

ln(1+ x) = x −

−

+... =

(−1)n−1

x (−1,1)

n=1

f (x) = (1+ x)

(биномиальный ряд).

α−1

α−2

f (0) =1, f '(x) =

α(1+ x)

, f '(0) = α ,

f "(x) = α(α −1)(1+ x)

, f "(0)

= α(α −1) , …,

(n)

(0) = α(α −1) ... (α − n +1) .

Следовательно, ряд Тейлора для функции

f (x) = (1+ x)

имеет вид

α(α −1)

... (α − n +1)

xn .

n=1

(15)

(16)

Ряд (16) называется биноминальным рядом. Радиус его сходимости

R = lim	a	n	= lim	α(α −1) ... (α − n +1)(n +1)!	= lim	n +1	=1.

	an+1			n!α(α −1) ... (α − n)		α − n
n→			n→		n→

Поскольку здесь трудно проверить выполнение условия теоремы 6, будем доказывать возможность разложения совершенно другим способом. Рассмотрим задачу Коши

(1+ x) y ' = αy

(17)

y(0) =1

193

Решаем данное уравнение (с разделяющимися переменными).

	(1+ x)	dy
	(1+ x)	dx
		dx

αy

;

dy y

= α	dx
	1	+ x

;

		dy
		y
		y

dx
= α	+ x
1

;

ln |

y |= α ln |1+ x | +ln | c2

;

ln |

y(x) \|= ln \| c (1 + x)	α
y(x) \|= ln \| c (1 + x)
2

;

y(x) = c	(1+ x)	α
y(x) = c	(1+ x)
2

;

y(x) = c y(0) = c

Теперь


(1+ x)	α	. Для нахождения постоянной c используем начальное условие
(1+ x)		. Для нахождения постоянной c используем начальное условие
=1 y(x) = (1+ x)			α	.
=1 y(x) = (1+ x)				.
докажем, что при				x (−1, 1)	сумма биноминального ряда (16) также

y(0) =1

является

решением этой задачи Коши. Для этого сначала подставим функцию (16) в уравнение (1+ x) y ' = αy (при этом ряд мы будем дифференцировать почленно, что, как и для всякого степенного ряда, возможно внутри интервала сходимости):

y =1+

α(α −1) ... (α − n +1)

y' =

α(α −1) ... (α − n +1)

xn−1 .

n=1

(n −1)!

Нам надо проверить выполнение равенства

(1+ x)

α(α −1)

... (α − n +1)

xn−1 = α + α

α(α −1) ... (α − n +1)

, или

n=1

(n −1)!

n=1

α(α −1)

... (α − n +1)

α(α −1) ... (α − n +1)

α(α −1) ... (α

− n

+1)

n−1

= = α + α

n=1

(n −1)!

n=1

(n −1)!

n=1

В первой сумме левой части этой формулы обозначим

n −1 = k ,

а затем (т.к.

индекс

суммирования можно обозначать любой буквой) вместо k

снова напишем

n :

α(α −1) ... (α − n)

α(α −1) ... (α − n +1)xn

= α + α α(α −1) ... (α − n

+1)xn .

n=0

n=1

(n −1)!

n=1

Чтобы доказать справедливость последнего равенства, достаточно проверить, что в нем совпадают коэффициенты при одинаковых степенях x слева и справа.

Коэффициент при

x	0

Коэффициент при x

, n = 1, 2,

...

α(α −1) ... (α − n)

α(α −1) ... (α − n +1)

;

(n −1)!

(α

−1) ... (α − n +1) .

α(α −1) ... (α − n) + α(α −1) ... (α − n +1)n = α

Вынося в левой части за скобку

α(α −1) ... (α − n +1) , имеем:

α(α −1) ... (α − n +1)(α − n + n) = α

(α

−1) ... (α − n +1)

что действительно верно.

Теперь подставим функцию (16) в начальное условие:

α(α −1)

... (α − n +1)

n=1

x=0

Но задача Коши (17) имеет единственное решение, поэтому функция (1+ x)α и сумма

биноминального ряда (16) должны совпадать, следовательно
	α(α −1) ... (α − n +1)		α(α −1)		x2		α(α −1)(α − 2)		x3 +... , (18)
(1+ x)α = 1+		xn = 1+ αx +				+
	n!		2!				3!
n=1
x (−1, 1) .
Замечание. При натуральных α		f (n) (x) = 0 при		n = α +1, α + 2,...,				следовательно,
биноминальный ряд превращается в конечную сумму,				содержащую α +1					слагаемых, а

равенство (18) превращается в формулу бинома Ньютона (естественно, при этом x R ).

Из полученных разложений (12) – (15) и (18) можно получать и другие разложения.

194

ЛЕКЦИЯ 3

РЯДЫ ФУРЬЕ

Ортогональные и ортонормированные системы функций

Определение 1. Функции

b f (x)g(x)dx = 0 .

f (x)

g(x)

называются ортогональными на отрезке

, если

Определение 2. Система функций					f1 (
	b
a,b , если		fm	(x) fn	(x)dx = 0, m n , т.е.

x), f2 (x),... называется ортогональной на отрезке

все функции системы ортогональны друг другу.

Определение 3.

отрезке a,b , если

Система функций

b fm (x) fn (x)dx = mn a

f (x), f		2	(x),...
1
0,	m n			.
=	m = n
1,

называется

ортонормированной на

Данные определения аналогичны определениям ортогональных и ортонормированных систем элементов евклидова пространства, в частности векторов двух или трехмерного пространства; роль скалярного произведения двух функций при этом выполняет интеграл от их произведения. Естественно, предполагается, что все такие интегралы существуют.

Далее докажем, что система функций 1, cos x ,

cos2x ,

cos3x ,…,

ортогональна на отрезке

−π, π

. Пусть m, n = 0,

1, ,2 ,

... , тогда

cos mx cos nxdx =

cos(m + n)x + cos(m − n)x dx =

sin(m +

2(m + n)

−π

sin(m − n) x

= 0, m n (так как sin πk = 0, k Z );

2(m − n)

−

cos(m − n)x − cos(m + n)x dx =

sin mx sin nxdx =

sin(m −

2(m − n)

−π

−

sin(m + n) x

= 0, m n (по той же причине);

2(m + n)

−π

sin mx cos nxdx =

sin(m + n)x + sin(m − n)x dx =

−

cos(m

−π

2(m + n)

sin x ,		sin
n) x	π	+
	−π

n) x −π π −

+ n) x	π	−
	−π

sin 3x

,…

−	1	cos(m − n) x π	= 0, m n (так как функция

	2(m − n)	−π

cos x

– четная); если же

	π		1	π		1
m = n, то		sin nx cos nxdx =	1		sin 2nxdx = −	1	π	= 0	(по той же причине);
m = n, то		sin nx cos nxdx =	2		sin 2nxdx = −	4n	cos 2nx \|−π	= 0	(по той же причине);
	−π		2	−π		4n
	−π			−π

функция 1 тоже входит в наши вычисления, так как 1 = cos m x m=0 .

Теперь посмотрим, не является ли наша система функций ортонормированной, т.е. в первых двух интегралах рассмотрим случай m = n :

195

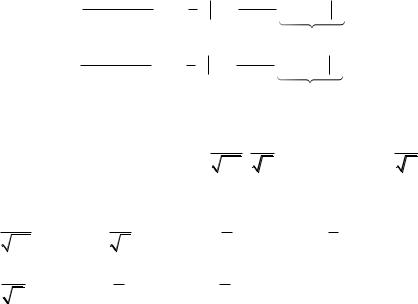
π		π	1	+ cos 2mx		1		1
	2	mxdx =	1	+ cos 2mx	dx =	1	π	1		π
cos	2						x −π +		sin 2m x
cos				2		2	x −π +	2 2m	sin 2m x	−π
−π		−π		2		2		2 2m
−π		−π							=0
									=0

,m = 1,2,…; m = 0 : π 1dx = 2π ;

−π

π		π	1	− cos 2mx		1		1
	2		1	− cos 2mx		1	π	1		π
sin	2	mxdx =			dx =		x −π −		sin 2m x
sin		mxdx =		2	dx =	2	x −π −	2 2m	sin 2m x	−π
−π		−π		2		2		2 2m
−π		−π							=0
									=0

= 1, 2, …

Отсюда следует, что наша система ортонормированной не является.

Проверим теперь, что система	1	,	1	cos mx, m =1, 2,...,	1	sin mx, m =1, 2,...
	2

ортонормированной на отрезке

−π, π

. Для этого рассмотрим интегралы:

dx =1,

cos mx dx =

cos

mxdx =

π =1

−π

2π

−π

sin mx

dx =

sin

mxdx =

=1 .

−

является

Ряд Фурье по произвольной ортонормированной системе функций. Тригонометрический ряд Фурье для функций с периодом 2π

Пусть	φn			ортонормированная на отрезке	a,b
		(x)
		n=1
возможность			представления заданной функции

система функций. Будет изучаться

f (x)

в виде разложения по

ортонормированной системе φn (x) , т.е. в виде суммы ряда

	n
n	n
c φ		(x)
n=1

. Пусть такое

представление возможно:

(x)

	n
n	n
c φ		(x)
n=1

(1)

Умножим равенство (1) на

φ	m	(x)
	m

и проинтегрируем от

до

. При этом предполагается,

что все приведенные ниже интегралы существуют и ряд возможно интегрировать почленно. Имеем:

	b			b
		f (x)φm (x)dx = cn			φn (x)φm (x)dx .
		f (x)φm (x)dx = cn			φn (x)φm (x)dx .
	a		n=1	a
	a			a
Так как система функций		φ	(x)
Так как система функций		n	ортонормированная, то все интегралы в правой части
этого равенства, в которых	n m , будут равны 0; тот же интеграл, в котором					n = m , будет
равен 1. Тогда из всей суммы в правой части останется только одно слагаемое							cm и

cm = b f (x)φm (x)dx . Заменяя в этом равенстве

на

, получаем, что если функция f (x)

представлена в виде разложения (1), то коэффициенты этого разложения обязательно ищутся по формулам

	b
cn =		f (x)φn	(x)dx, n =1, 2,...	(2)

Определение 4. Ряд cnφn (x) с коэффициентами (2) называется рядом Фурье функции

n=1

f (x) . Числа cn называются коэффициентами Фурье этой функции.

196

Теперь обратимся к так называемому тригонометрическому ряду

ортонормированной на отрезке							−π, π	системе функций
ортонормированной на отрезке								системе функций
			1	,	1	cos mx, m =1, 2,...,			1	sin mx, m =1, 2,....
			2π	,	π	cos mx, m =1, 2,...,			π	sin mx, m =1, 2,....
			2π		π				π
Функция		f (x)	будет предполагаться абсолютно интегрируемой на
π	f (x) dx	существует.
−π

Фурье, т.е. ряду по

−π, π , т.е. такой, что

Если обозначить в представлении (1) коэффициенты при косинусах и синусах как cn и cn соответственно, то это представление приобретает вид:

				1
			0
	f (x) = c			2π	+
				2π		n=1
Положим
c	1	=	a	; c	1		=
c		=	0	; c			=
			0
0	2π		2	n		π
	2π		2			π

Тогда последняя формула примет вид:

c	1
c
n	π
	π
a	, c
n	n

cos nx + c
		n
1	= b	, n

π	n

1 π

=1,

sinnx

2,... .

	a
	a	+ (an	cos nx + bn sin nx) .
f (x) =	0
f (x) =	2
	2	n=1
		n=1

Из (2) следует, что коэффициенты этого разложения ищутся по формулам

+π

f (x)

f (x)dx;

dx =

2π

−π

2π

−π

f (x)

cos nxdx =

f (x) cos nxdx, n =1, 2,...;

−π

f (x)

sin nxdx =

f (x) sin nxdx, n =1, 2,...

−π

(3)

(4)

f (x) cos nxdx, n = 0,1, 2..., b =

f (x)sin nxdx, n =1, 2,....

(5)

−π

(смысл обозначения первого коэффициента как

состоит в том, что a0 ищется по той же

формуле,

что

an ,

n = 1,2,

…;

интегралы

существуют, так

как

f (x) cos nx

f (x) ,

f (x)sin nx f (x) ,

а f (x) на − , абсолютно интегрируема).

Определение 5. Ряд в правой части формулы (4) с коэффициентами (5) (независимо от того, сходится ли он и чему равна его сумма) называется тригонометрическим рядом Фурье функции f (x) . Числа an и bn при этом называются коэффициентами Фурье этой функции.

Теперь обратимся к возможности разложения функции в ряд Фурье. Отметим, что если представление (4) возможно, то f (x) является периодической функцией с периодом 2π : f (x + 2π) = f (x), x R (так как этот период имеют все функции cos nx и sin nx ).

Для того чтобы сформулировать теоремy о достаточных условиях возможности разложения функции в ряд Фурье, дадим сначала следующее определение.

197

Определение 6. Функция

f (x)

называется кусочно-монотонной на отрезке a,

отрезок	можно разбить конечным числом точек	x1 , x2 ,..., xn−1	на
(a, x1), (x1	, x2 ),..., (xn−1,b) так, что на каждом из этих интервалов функция будет
т.е. либо невозрастающей, либо неубывающей.

Такая функция будет абсолютно интегрируемой на отрезке a,b .

b , если этот интервалы монотонной,

Теорема 1. (признак Дирихле – достаточные условия разложения функции в ряд Фурье). Пусть y = f (x) – периодическая (с периодом 2π ), кусочно-монотонная на отрезке

	−π, π		и имеющая на нем лишь конечное число точек разрыва (причем, первого рода)

функция. Сопоставим ей ряд Фурье (~ это знак сопоставления):

где

					a
				f (x)~	0	+
				f (x)~	2	+
					2
		1	π
n	=	1				n
n						n
a		π		f (x) cos nxdx, n = 0,1, 2,..., b
		π	−π
			−π

(an

n=1

1 π

=π −π

cos nx + f (x) sin

bn sin nxdx,

nx) n =

1, 2,...

(как уже отмечено выше, эти интегралы существуют).

Тогда наш ряд Фурье сходится во всех точках, причем сумма этого ряда равна

f (x) в точках непрерывности функции			f ,

f (x − 0)	+ f (x + 0)	в точках разрыва функции		f .
		в точках разрыва функции		f .
	2

Последний случай изображен на рис. 1.

•

Рисунок 1

Отметим, что выражение

так как в этих точках	f (

f (x − 0) + f (x + 0)

2
x − 0) + f (x + 0)	=	f
2	=
2

дает и сумму ряда в точках непрерывности f ,

	(x) + f (x)	= f (x) .
	2	= f (x) .
	2

Доказательство этой теоремы, в силу его сложности и отсутствия достаточного для такого доказательства времени в курсе высшей математики технических вузов, мы оставим за пределами данных лекций.

Коэффициенты Фурье четных и нечетных функций

1) Пусть функция				y = f (x) четная, тогда (функция sin nx
	π
b =	1	π	f (x) sin nxdx = 0 ,		n =1, 2,3,... , так как интеграл

n

−π нечётная

нечетная)

от нечетной функции в

симметричных пределах равен нулю;
a =	1 π		f (x) cos nxdx =	2	π	f (x) cos nxdx ,	n = 0, 1, 2, … по свойству интеграла от четной
	π			π

n
		−π	чётная		0
			чётная

функции в симметричных пределах.

198

2) Пусть

		1	π
an	=
		π
			−π

функция	y = f (x) нечетная, тогда (функция
f (x) cos nxdx = 0 , n = 0,1, 2,... ;
нечётная

cos nx

четная)

b =

f (x) sin nxdx =

f (x) sin nxdx , n =1, 2,3,... по тем же причинам, что выше.

−π

чётная

+ (an

Таким образом, в формуле f (x)~

cos nx + bn sin nx) для четной функции bn

= 0

, т.е.

n=1

четная функция раскладывается только по четным функциям cos nx ; для нечетной функции an = 0 , т.е. нечетная функция раскладывается только по нечетным функциям sin nx .

Примеры.

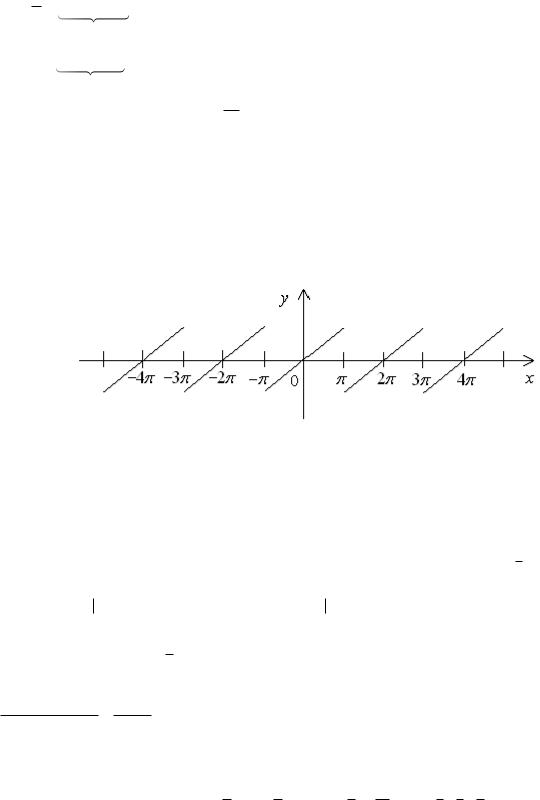
1. Разложить в ряд Фурье на отрезке −π, π функцию y = x .

Решение. Эта функция вообще не является периодической, поэтому рассмотрим новую периодическую (с периодом 2π ) функцию f (x) , которая на −π, π совпадает с данной (рис. 2).

Рисунок 2

Значения функции в точках разрыва первого рода

π, 3π, 5π, ... можно взять любыми.

Эта функция удовлетворяет всем условиям нашей теоремы ( T = 2π

, возрастает на

−π, π

, разрывы первого рода в

точках π ), следовательно, ее можно разложить в ряд Фурье. Но при

x (−π, π) она совпадает с данной функцией y = x,

тогда для x (−π, π)

получим разложение функции

y = x .

Наша функция нечетная, значит,

an = 0 , n = 0, 1, 2, …; bn =

x sin nxdx ;

sin nxdx = dv v = −

cos nx

n +1 2

bn = −

x cos n x 0

cos nxdx = −

π cos πn +

sin n x 0

= (−1)

, n = 1, 2, ...

πn

( −1)

πn

Следовательно,

f ( x)~ (−1)

n +1

sin nx .

n =1

При этом,

по

теореме

1, сумма ряда

равна

f (x)

в точках

непрерывности

, т.е.

при

x π, 3π, 5π, ... и

f ( x − 0) +

f ( x + 0)

1 + (−1)

= 0

в точках разрыва

π, 3π, 5π... (что, впрочем, видно и из самого ряда), тогда для

2 sin nx .

x (−π, π)

f ( x) = x = (−1)n +1

n =1

n +1

πn

Замечание. Положим в этом равенстве

x =

, тогда

= (−1)

sin

= 2 1 −

−

+ ...

; отсюда имеем один

n =1

=0 , 1

из способов приближенного нахождения числа π :

π = 4(1 −

−

+ ...) .

199

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 1920 / 2520 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете Высшая математика

#
01.06.20245.04 Mб1L_D_Kudryavtsev_Kurs_matimaticheskogo_analiza_Tom_1.pdf
#
01.06.20246.08 Mб0L_D_Kudryavtsev_Kurs_matimaticheskogo_analiza_Tom_2.pdf
#
01.06.20242.46 Mб0L_D_Kudryavtsev_Kurs_matimaticheskogo_analiza_Tom_3.pdf
#
01.06.20241.39 Mб5вышмат полезно.pdf
#
01.06.2024482.88 Кб2кр по алегебре.pdf
#
01.06.20245.41 Mб59лекции вышмат.pdf
#
01.06.20241.34 Mб1линейная алгебра и агалитич геом.pdf