6.2. Распределение Пуассона

Как было уже отмечено, биномиальное распределение приближается к нормальному при n. Однако это не имеет места, если наряду с увеличением n одна из величин p или q стремится к нулю. В этом случае имеет место асимптотическая формула Пуассона, т.е. при n, p0

, (6.7)

где =np. Эта формула определяет закон распределения Пуассона, который имеет самостоятельное значение, а не только как частный случай биномиального распределения. В отличие от биномиального распределения здесь случайная величина k может принимать бесконечное множество значений: k=0,1,2,…

Закон Пуассона описывает число событий k, происходящих за одинаковые промежутки времени при условии, что события происходят независимо друг от друга с постоянной средней интенсивностью, которая характеризуется параметром . Многоугольник распределения Пуассона показан на рис. 6.2. Отметим, что при больших  расп

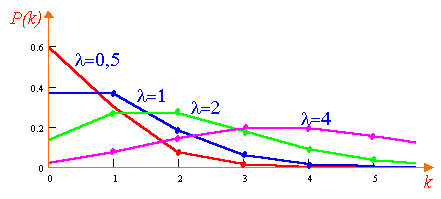Рис. 6.2

ределение Пуассона приближается к нормальному. Поэтому распределение Пуассона применяется, как правило, в тех случаях, когда имеет порядок единицы, при этом число испытаний n должно быть велико, а вероятность появления события p в каждом испытании мала. В связи с этим закон Пуассона часто называют еще законом распределения редких явлений.

Примерами ситуаций, в которых возникает распределение Пуассона, могут служить распределения: 1) числа определенных микробов в единице объема; 2) числа вылетевших электронов с накаленного катода за единицу времени; 3) числа -частиц, испускаемых радиоактивным источником за определенных промежуток времени; 4) числа вызовов, поступающих на телефонную станцию за определенное время суток и т.д.

Запишем закон Пуассона в виде таблицы

X	0	1	2	3	…	k	…
P					…		…

Проверим, что сумма всех вероятностей равна единице:

Найдем числовые характеристики этого распределения. По определению математического ожидания для ДСВ имеем

.

Отметим, что в последней сумме суммирование начинается с k=1, т.к. первый член суммы, соответствующий k=0, равен нулю.

Для нахождения дисперсии найдем предварительно математического ожидание квадрата случайной:

Тогда

Таким образом, математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона, совпадают и равны параметру этого распределения

. (6.8)

В этом состоит отличительная особенность распределения Пуассона. Так, если на основании опытных данных было получено, что математическое ожидание и дисперсия некоторой величины близки между собой, то есть основания предполагать, что данная случайная величина распределена в соответствии с законом Пуассона.

Воспользовавшись понятием начальных и центральных моментов, можно показать, что для распределения Пуассона коэффициент асимметрии и эксцесс равны:

. (6.9)

Поскольку параметр  всегда положителен, то у распределения Пуассона всегда положительная асимметрия и эксцесс.

Покажем теперь, что формулу Пуассона можно рассматривать как математическую модель простейшего потока событий.

Потоком событийназывают последовательность событий, которые наступают в случайные моменты времени. Поток называетсяпростейшим, если он обладает свойствамистационарности,отсутствия последействияиординарности.

Интенсивностью потока  называют среднее число событий, которые появляются в единицу времени.

Если постоянная интенсивности потока  известна, то вероятность появления k событий простейшего потока за время t определяется формулой Пуассона:

. (6.10)

Эта формула отражает все свойства простейшего потока. Более того, любой простейший поток описывается формулой Пуассона, поэтому простейшие потоки часто называют пуассоновскими.

Свойство стационарности состоит в том, что вероятность появления k событий в любом промежутке времени зависит только от числа k и от длительности t промежутка времени и не зависит от начала его отсчета. Другими словами, если поток обладает свойством стационарности, то вероятность появления k событий за промежуток времени t есть функция, зависящая только от k и от t.

В случае простейшего потока из формулы Пуассона (6.10) следует, что вероятность k событий за время t, при заданной интенсивности является функцией только двух аргументов: k и t, что характеризует свойство стационарности.

Свойство отсутствия последействия состоит в том, что вероятность появления k событий в любом промежутке времени зависит от того, появлялись или не появлялись события в моменты времени, предшествующие началу рассматриваемого промежутка. Другими словами, предыстория потока не влияет на вероятности появления событий в ближайшем будущем.

В случае простейшего потока в формуле Пуассона (6.10) не используется информация о появлении событий до начала рассматриваемого промежутка времени, что характеризует свойство отсутствия последействия.

Свойство ординарности состоит в том, что появление двух или более событий за малый промежуток времени практически невозможно. Другими словами, вероятность появление более одного события за малый промежуток времени пренебрежимо мала по сравнению с вероятностью появления только одного события.

Покажем, что формула Пуассона (6.10) отражает свойство ординарности. Положив k=0 и k=1, найдем соответственно вероятности не появления событий и появления одного события:

Следовательно, вероятность появления более одного события равна

.

Используя разложение функции в ряд Маклорена, после элементарных преобразований получим

.

Сравнивая P_t(1) и P_t(k>1), заключаем, что при малых значениях t вероятность появления более одного события пренебрежимо мала по сравнению с вероятностью наступления одного события, что характеризует свойство ординарности.

Пример 6.2. В наблюдениях Резерфорда и Гейгера радиоактивное вещество за промежуток времени 7,5 сек испускало в среднем 3,87 -частицы. Найти вероятность того, что за 1 сек это вещество испустит хотя бы одну частицу.

Решение. Как мы уже отмечали, распределение числа -частиц, испускаемых радиоактивным источником за определенных промежуток времени описывается формулой Пуассона, т.е. образует простейший поток событий. Поскольку интенсивность испускания -частиц за 1 сек равно

,

то формула Пуассона (6.10) примет вид

Таким образом, вероятность того, что за t=1 сек вещество испустит хотя бы одну частицу будет равно

.