ТЕМА 3.3. Суперпозиционные методы анализа передачи и |
|
преобразования сигналов линейными цепями. |
|
Содержание |
|
Переходная и импульсная характеристики линейной цепи..................................... |
1 |
Операторные уравнения для временных характеристик.......................................... |
3 |
Связь между характеристиками линейной цепи........................................................ |
3 |
Временные характеристики типовых радиотехнических звеньев. |
|
Дифференцирующее звено. ......................................................................................... |
6 |
Общие положения суперпозиционных методов анализа........................................ |
13 |
Спектральный метод анализа.................................................................................... |
14 |
Условия неискажающей передачи сигнала через линейную цепь. ....................... |
16 |
Временной суперпозиционный метод анализа с использованием характеристики |
|
цепи. Метод интеграла свертки................................................................................. |
19 |
Временной суперпозиционный метод анализа с использованием переходной |
|
характеристики цепи. Метод интеграла Дюамеля. ................................................. |
21 |
Отклик линейной цепи x(t) на воздействие s(t) зависит от вида воздействия, начальных условий и свойств цепи. Свойства цепи определяются схемой и параметрами элементов. Если необходимо произвести сравнение свойств нескольких электрических цепей, то, очевидно, воздействие и начальные условия должны быть типовыми.
Чтобы можно было сравнивать свойства различных цепей и определять отклик цеп на воздействие, изменяющееся по произвольному закону, вводят так называемые временные характеристики цепей. Их получают как отклики цепей на воздействия вида: l(t) и б(t) при нулевых начальных условиях.
Это единичная функция (функция включения):
1( t) = {0 |
при |
t <0: |
1 |
при t ≥0 |
|
и дельта функция: |
|
|
s( t) ={0 |
при |
t≠0: |
∞ |
при |
t=0 |
и∞∫δ (t) dt = 1
−∞
Таким образом, временные характеристики линейной цепи - это реакция данной цепи на типовое внешнее воздействие, ее отклик.
Переходная и импульсная характеристики линейной цепи.
В зависимости от вида типового воздействия различают две временные характеристики: переходную и импульсную (весовую функцию цепи).
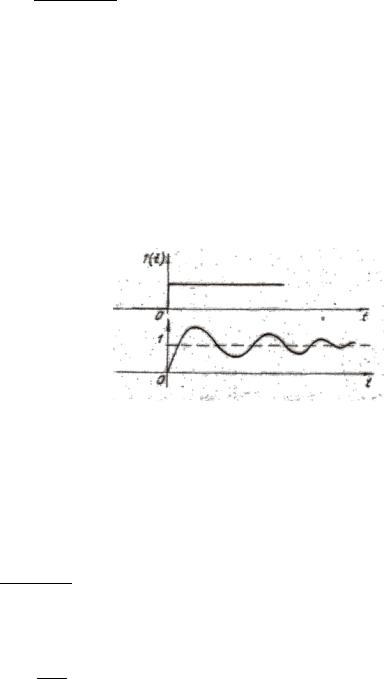
Переходной характеристикой (ПХ) линейной системы называют функцию, численно равную реакции пустой линейной цепи на единичный сигнал включения.
Внешнее воздействие s(t)=A*l(t),
где A-величина скачка напряжения или тока.
Реакция цепи x(t)=x A*l(t)
Переходная характеристика определяется:
h(t) = x A1(t) (8.15)
A
Допустим A=l, тогда h(t)=x1(t).
Но это численное равенство, а размерность равна отношению размерностей выходной и входной величин.
Если, например, [A*l(t)]=B, а [x a*l(t)]=B, то [h(t)]-безразмерная; |
||||
[A1(t)]= B, а[x |
A1(t) |
]= A, тт[h(t)]= |
1 |
=OM |
|
||||
|
OM |
|||
[A1(t)]=, A а [xA1(t ) ] |
= A, тт [h(t)]= OM |
|||
Физический смысл переходной характеристики (рис.8.16) заключен в том, что она описывает становление процесса в цепи при подключении ее к источнику постоянного напряжения в IB или к источнику постоянного тока в IA.
Рис.8.16.
Импульсной характеристикой (ИХ) линейной цепи называют функцию, численно равную реакции пустой линейной цепи на входное воздействие в виде б-функции.
Определяют ИХ так. Берут внешнее воздействие в виде s(t)=Aб(t) и подают на вход исследуемой цепи.
Тогда xAδ (t ) = g(t)- импульсная характеристика цепи.
A
при A=1ИХ g(t)=xA*б(l) .
Можно определить ИХ g(t) и другим путем:
g(t) = dtd h(t).
На практике так чаще всего и делается. Размерность g(t) равна размерности h(t), деленной на секунду,
[g (t )]= [h(t )]
C
Операторные уравнения для временных характеристик.
По определению переходная характеристика цепи h(t) = xA1(t ) ,
A
импульсная переходная характеристика цепи g(t) = xAδ (t )
A
XA*l(t) и XA*б(t) – реакции цепи на сигналы s(t), равные соответственно A*l(t) и A*б(t). Еще их можно записать:
~
xA1(t ) = K ( jω) A1(t) и
~Aδ (t ) = ( ω) δ ( ) x K j A t
Тогда,
~
h (t) = K ( jω)1(t) (8.16)
~( ) = ( ω)δ ( ) (8.17) g t K j t
Применив к выражениям (8.16) и (8.17) преобразование Лапласа, получим:
H ( p) = |
K ( p) |
; |
(8.18) |
|
p |
|
|
G( p) = K ( p). |
|
(8.19) |
|
Таким образом, изображение переходной характеристики цепи равно передаточной функции цепи K(p), деленной на p/
Изображение импульсной характеристики равно самой передаточной функции цепи.
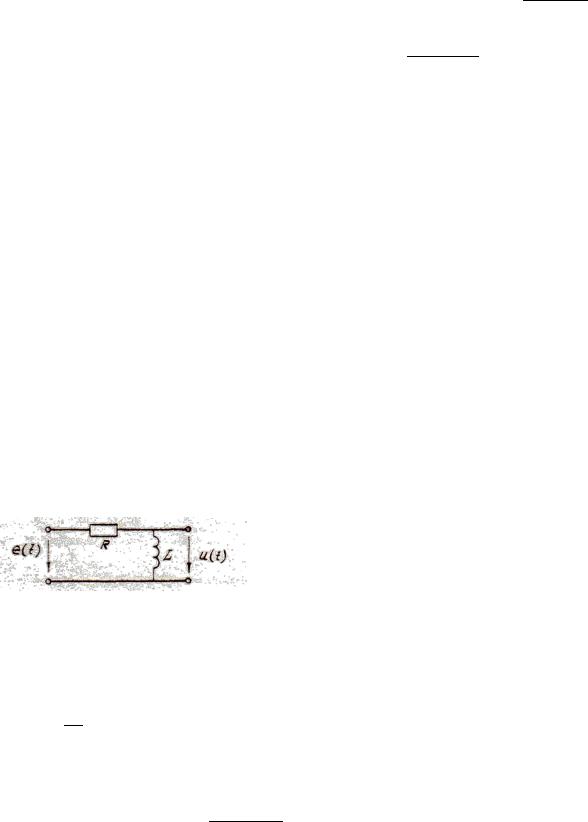
Например, имеется цепь (рис.8.17). Необходимо определить H(p) и G(p).
Рис.8.17.
Решение:
K ( jω) =
гдеτ = RL ;
jωL |
|
; K ( p) = |
pL |
|
|
|
|
||||
R + jωL |
R + pL |
|
|
||||||||
|
|
|
|
|
|||||||
H ( p) = |
K ( p) |
|
pL 1 |
|
|
1 |
|
||||
|
= |
|
|
|
|
= |
|
|
|||
p |
|
|
|
|
1 |
||||||
|
|
R + pL p |
|
|
p + |
||||||
|
|
|
|
|
|
|
|
|
|
τ |
|
G( p) = K ( p) = p p 1 .
+ τ
Связь между характеристиками линейной цепи.
Характеристики линейной цепи (передаточная, переходная и импульсная) численно выражают реакции пустой цепи на стандартные сигналы. Связь между любым из этих сигналов и реакций цепи на него устанавливается линейным дифференциальнымуравнением.Дифференциальноеуравнение,неразрушающее
линейной связи между сигналами на входе и выходе цепи, будет одно и то же для любого из этих сигналов. Если внешнее воздействие может быть представлено линейной формой некоторых величин (суммой, интегралом, производной и т.д.), то реакция цепи может быть той же линейной формой ее реакций на воздействия, выражаемые этими величинами.
Все стандартные сигналы линейно связаны между собой. Так дельта - функции и сигнал включения связаны соотношениями:
δ (t) = |
d |
1(t); |
(8.20) |
||||
|
|
||||||
|
|
dt |
|
|
|||
t |
δ (t) = |
d |
1(t); |
(8.21) |
|||
∫ |
|||||||
dt |
|||||||
0 |
|
|
|
|
|||
Связьмеждудельтафункциейигармоническимсигналомустанавливается обратным преобразованием Фурье для функции б(t). Спектральная плотность дельта - импульса: Sб(ω )=1
Гармонический сигнал представляется как e j ω t Для сигнала б(t)
|
|
1 |
|
|
∞ |
|
|
|
||
δ (t) = |
|
|
∫e jωt dω (8.22) |
|||||||
2π |
||||||||||
|
|
−∞ |
||||||||
Подобным образом,учитывая спектральную плотность единичного сигнала |
||||||||||
l(t) |
|
1 |
|
|
||||||
S (t)(ω) = |
, |
|
||||||||
|
||||||||||
1 |
|
|
|
|
|
jω |
||||
можем записать: |
|
|||||||||
|
|
e jωt |
||||||||
|
|
1 ∞ |
||||||||
1(t) = |
|
−∞∫ |
|
dω. (8.23) |
||||||
2π |
jω |
|||||||||
если все стандартные сигналы линейно связаны между собой, то и реакции на них так же взаимосвязаны. Будем исходить из передаточной характеристики K(j), которая позволяет записать реакцию цепи на стандартное воздействие e jω t
в виде K(jω )* e jω t.
Учитывая выражения (8.22) и (8.23), записываем:
|
1 |
|
∞ |
K ( jω) |
jωt |
|
|
h(t) = |
|
|
|
−∞∫ |
jω e |
|
dω; (8.24) |
2π |
|
||||||
|
1 |
|
∞ |
|
|
|
|
g(t) = |
|
∫ K ( jω)e jωt dω; (8.25) |
|||||
|
|
|
|||||
|
|
2π −∞ |
|
|
|
||
Полученные соотношения рассматриваем как обратные преобразования Фурье для сигналов h(t) и g(t), которые имеют соответственно спектральные плотности:
K( jω) ÷h(t); jω
K( jω) ÷ g(t). jω
Тогда:
Искомые |
|
|
|
|
|
|
Известные характеристики цепи |
||||
характеристики |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
K( jω) |
|
h(t) |
g(t) |
||||
цепи |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||
K( jω) |
|
|
|
|
|
K( jω) |
|
∞ |
∞ |
||
|
|
|
|
|
|
|
|
|
|
jω∫h(t)e− jωt dt |
∫g(t)e− jωt dt |
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
h(t) |
|
1 |
|
∞ |
|
|
h(t) |
t |
||
|
|
|
|
∫ K |
( jω) e jωt dω |
|
∫g(t)dt |
||||
|
|
|
|
2π |
|
||||||
|
|
|
|
−∞ |
jω |
|
|
0− |
|||
|
|
|
|
|
|
|
|
|
|||
|
g(t) |
|
|
|
|
|
|
|
|
′ |
g(t) |
|
|
1 |
|
∞ |
|
|
h (t) |
||||
|
|
|
|
∫K( jω)e jωt dω |
|
|
|||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
2π −∞ |
|
|
|
|
||
|
K( jω) |
= ∞∫h(t)e− jωt dt |
|
|
|
|
|||||
|
jω |
0 |
|
|
|
|
|
|
|
|
|
или |
K( jω) |
|
∞ |
|
|
|
(8.26) |
|
|
||
|
= jω∫h(t)e− jωt dt |
|
|
||||||||
|
jω |
0 |
|
|
|
|
|
|
|
|
|
K ( jω) = ∞∫g(t)e− jωt dt |
(8.27) |
|
|
||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
Соотношения (8.26) и (8.27) выражают связь между передаточной характеристикой цепи K(jω ), переходной h(t) и импульcной g(t) характеристиками этой же цепи.
Выражение (8.27) имеет простое физическое толкование, указывающее , что спектр дельта -импульса преобразуется линейной цепью в спектр, тождественный ее передаточной характеристике. Это и понятно, так как спектр дельта - импульса равномерный [Sб(w)=1] и не имеет начальных фазовых сдвигов гармонических составляющих (рис.8.18). после прохождения через цепь сигнал приобретает неравномерность амплитудно-частотного спектра и фазовые сдвиги, определяемые передаточной характеристикой цепи.
Рис.8.18.
Связь между h(t) и g(t) устанавливается из выражений (8.20) и (8.21). Так как цепь линейна, то реакция ее на эти сигналы:
g(t) = |
dh(t) |
, |
(8.28) |
|
|
||||
|
|
dt |
|
|
h(t) = ∫t |
g(t)dt |
(8.29) |
||
0 |
|
|
|
|
Полученные соотношения показывают, что достаточно определить любую из трех характеристик цепи, а по ней уже можно получить остальные (табл.8.2).