
- •Об авторе
- •Предисловие
- •Для кого эта книга
- •О чем эта книга
- •Что вам потребуется при чтении этой книги
- •Условные обозначения
- •От издательства
- •Глава 1. Обзор алгоритмов
- •Что такое алгоритм
- •Этапы алгоритма
- •Определение логики алгоритма
- •Псевдокод
- •Использование сниппетов
- •Создание плана выполнения
- •Введение в библиотеки Python
- •Библиотеки Python
- •Реализация Python с помощью Jupyter Notebook
- •Методы разработки алгоритмов
- •Параметры данных
- •Параметры вычислений
- •Анализ производительности
- •Анализ пространственной сложности
- •Анализ временной сложности
- •Оценка эффективности
- •Выбор алгоритма
- •«О-большое»
- •Проверка алгоритма
- •Точные, приближенные и рандомизированные алгоритмы
- •Объяснимость алгоритма
- •Резюме
- •Глава 2. Структуры данных, используемые в алгоритмах
- •Структуры данных в Python
- •Список
- •Кортеж
- •Словарь
- •Множество
- •DataFrame
- •Матрица
- •Абстрактные типы данных
- •Вектор
- •Стек
- •Очередь
- •Базовый принцип использования стеков и очередей
- •Дерево
- •Резюме
- •Глава 3. Алгоритмы сортировки и поиска
- •Алгоритмы сортировки
- •Обмен значений переменных в Python
- •Сортировка пузырьком
- •Сортировка вставками
- •Сортировка слиянием
- •Сортировка Шелла
- •Сортировка выбором
- •Алгоритмы поиска
- •Линейный поиск
- •Бинарный поиск
- •Интерполяционный поиск
- •Практическое применение
- •Резюме
- •Глава 4. Разработка алгоритмов
- •Знакомство с основными концепциями разработки алгоритма
- •Вопрос 1. Даст ли разработанный алгоритм ожидаемый результат?
- •Вопрос 2. Является ли данный алгоритм оптимальным способом получения результата?
- •Вопрос 3. Как алгоритм будет работать с большими наборами данных?
- •Понимание алгоритмических стратегий
- •Стратегия «разделяй и властвуй»
- •Стратегия динамического программирования
- •Жадные алгоритмы
- •Практическое применение — решение задачи коммивояжера
- •Использование стратегии полного перебора
- •Использование жадного алгоритма
- •Алгоритм PageRank
- •Постановка задачи
- •Реализация алгоритма PageRank
- •Знакомство с линейным программированием
- •Практическое применение — планирование производства с помощью линейного программирования
- •Резюме
- •Глава 5. Графовые алгоритмы
- •Представление графов
- •Типы графов
- •Особые типы ребер
- •Эгоцентрические сети
- •Анализ социальных сетей
- •Введение в теорию сетевого анализа
- •Кратчайший путь
- •Создание окрестностей
- •Показатели центральности
- •Вычисление показателей центральности с помощью Python
- •Понятие обхода графа
- •BFS — поиск в ширину
- •DFS — поиск в глубину
- •Практический пример — выявление мошенничества
- •Простой анализ мошенничества
- •Анализ мошенничества методом сторожевой башни
- •Резюме
- •Глава 6. Алгоритмы машинного обучения без учителя
- •Обучение без учителя
- •Обучение без учителя в жизненном цикле майнинга данных
- •Современные тенденции исследований в области обучения без учителя
- •Практические примеры
- •Алгоритмы кластеризации
- •Количественная оценка сходства
- •Иерархическая кластеризация
- •Оценка кластеров
- •Применение кластеризации
- •Снижение размерности
- •Метод главных компонент (PCA)
- •Ограничения PCA
- •Поиск ассоциативных правил
- •Примеры использования
- •Анализ рыночной корзины
- •Ассоциативные правила
- •Оценка качества правила
- •Алгоритмы анализа ассоциаций
- •Практический пример — объединение похожих твитов в кластеры
- •Тематическое моделирование
- •Кластеризация
- •Алгоритмы обнаружения выбросов (аномалий)
- •Использование кластеризации
- •Обнаружение аномалий на основе плотности
- •Метод опорных векторов
- •Резюме
- •Глава 7. Традиционные алгоритмы обучения с учителем
- •Машинное обучение с учителем
- •Терминология машинного обучения с учителем
- •Благоприятные условия
- •Различие между классификаторами и регрессорами
- •Алгоритмы классификации
- •Задача классификации
- •Оценка классификаторов
- •Этапы классификации
- •Алгоритм дерева решений
- •Ансамблевые методы
- •Логистическая регрессия
- •Метод опорных векторов (SVM)
- •Наивный байесовский алгоритм
- •Алгоритмы регрессии
- •Задача регрессии
- •Линейная регрессия
- •Алгоритм дерева регрессии
- •Алгоритм градиентного бустинга для регрессии
- •Среди алгоритмов регрессии победителем становится...
- •Практический пример — как предсказать погоду
- •Резюме
- •Глава 8. Алгоритмы нейронных сетей
- •Введение в ИНС
- •Эволюция ИНС
- •Обучение нейронной сети
- •Анатомия нейронной сети
- •Градиентный спуск
- •Функции активации
- •Инструменты и фреймворки
- •Keras
- •Знакомство с TensorFlow
- •Типы нейронных сетей
- •Перенос обучения
- •Практический пример — использование глубокого обучения для выявления мошенничества
- •Методология
- •Резюме
- •Глава 9. Алгоритмы обработки естественного языка
- •Знакомство с NLP
- •Терминология NLP
- •Библиотека NLTK
- •Мешок слов (BoW)
- •Эмбеддинги слов
- •Окружение слова
- •Свойства эмбеддингов слов
- •Рекуррентные нейросети в NLP
- •Использование NLP для анализа эмоциональной окраски текста
- •Практический пример — анализ тональности в отзывах на фильмы
- •Резюме
- •Глава 10. Рекомендательные системы
- •Введение в рекомендательные системы
- •Типы рекомендательных систем
- •Рекомендательные системы на основе контента
- •Рекомендательные системы на основе коллаборативной фильтрации
- •Гибридные рекомендательные системы
- •Ограничения рекомендательных систем
- •Проблема холодного старта
- •Требования к метаданным
- •Проблема разреженности данных
- •Предвзятость из-за социального влияния
- •Ограниченные данные
- •Области практического применения
- •Практический пример — создание рекомендательной системы
- •Резюме
- •Глава 11. Алгоритмы обработки данных
- •Знакомство с алгоритмами обработки данных
- •Классификация данных
- •Алгоритмы хранения данных
- •Стратегии хранения данных
- •Алгоритмы потоковой передачи данных
- •Применение потоковой передачи
- •Алгоритмы сжатия данных
- •Алгоритмы сжатия без потерь
- •Практический пример — анализ тональности твитов в режиме реального времени
- •Резюме
- •Глава 12. Криптография
- •Введение в криптографию
- •Понимание важности самого слабого звена
- •Основная терминология
- •Требования безопасности
- •Базовое устройство шифров
- •Типы криптографических методов
- •Криптографические хеш-функции
- •Симметричное шифрование
- •Асимметричное шифрование
- •Практический пример — проблемы безопасности при развертывании модели МО
- •Атака посредника (MITM)
- •Избежание маскарадинга
- •Шифрование данных и моделей
- •Резюме
- •Глава 13. Крупномасштабные алгоритмы
- •Введение в крупномасштабные алгоритмы
- •Определение эффективного крупномасштабного алгоритма
- •Терминология
- •Разработка параллельных алгоритмов
- •Закон Амдала
- •Гранулярность задачи
- •Балансировка нагрузки
- •Проблема расположения
- •Запуск параллельной обработки на Python
- •Разработка стратегии мультипроцессорной обработки
- •Введение в CUDA
- •Кластерные вычисления
- •Гибридная стратегия
- •Резюме
- •Глава 14. Практические рекомендации
- •Введение в практические рекомендации
- •Печальная история ИИ-бота в Твиттере
- •Объяснимость алгоритма
- •Алгоритмы машинного обучения и объяснимость
- •Этика и алгоритмы
- •Проблемы обучающихся алгоритмов
- •Понимание этических аспектов
- •Снижение предвзятости в моделях
- •Решение NP-трудных задач
- •Упрощение задачи
- •Адаптация известного решения аналогичной задачи
- •Вероятностный метод
- •Когда следует использовать алгоритмы
- •Практический пример — события типа «черный лебедь»
- •Резюме
164 |
Глава 6. Алгоритмы машинного обучения без учителя |
|
|
|
|
|
|
|
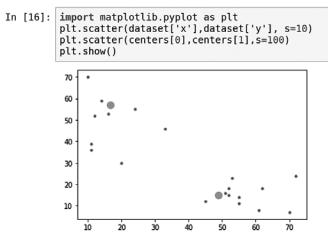
Рис. 6.10
Обратите внимание, что большие точки на графике являются центроидами, которые определил алгоритм k-средних.
Ограничения кластеризации методом k-средних
Алгоритм k-средних разработан как простой и быстрый алгоритм. Но из-за преднамеренной простоты в архитектуре он имеет ряд ограничений:
zz Самое большое ограничение: количество кластеров должно быть заранее определено.
zz Первоначальное назначение центров кластеров является случайным. Таким образом, при каждом запуске алгоритм может давать несколько разные кла стеры.
zz Каждая точка данных привязывается только к одному кластеру. zz Кластеризация методом k-средних чувствительна к выбросам.
Иерархическая кластеризация
Кластеризация методом k-средних реализует подход «сверху вниз», так как мы начинаем алгоритм с наиболее важных точек данных, которые служат центрами кластеров. Существует альтернативный подход к кластеризации, при котором вместо того, чтобы начинать сверху, мы запускаем алгоритм снизу. «Внизу» в этом контексте находится каждая отдельная точка данных в пространстве задачи.
Алгоритмы кластеризации |
165 |
Метод заключается в том, чтобы группировать похожие точки данных вместе по мере продвижения к центрам кластера. Подход «снизу вверх» используется ал горитмами иерархической кластеризации. Давайте рассмотрим его подробнее.
Этапы иерархической кластеризации
Иерархическая кластеризация состоит из следующих шагов:
1.Создаем отдельный кластер для каждой точки данных. Если наше простран ство задачи состоит из 100 точек данных, то алгоритм начнет со 100 класте ров.
2.Группируем только ближайшие друг к другу точки.
3.Проверяем условие остановки; если оно еще не выполнено, то повторяем шаг 2.
Полученная кластерная структура называется дендрограммой.
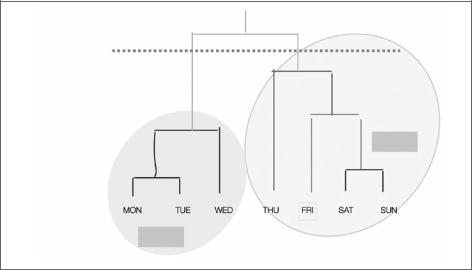
В дендрограмме высота вертикальных линий показывает, насколько близко расположены элементы (рис. 6.11).
2
1
Рис. 6.11
Обратите внимание, что условие остановки показано пунктирной линией на рисунке выше.

166 |
Глава 6. Алгоритмы машинного обучения без учителя |
Кодирование алгоритма иерархической кластеризации
Теперь давайте реализуем иерархический алгоритм на Python:
1.Сначала импортируем AgglomerativeClustering из библиотеки sklearn. cluster, а также пакеты pandas и numpy:
from sklearn.cluster import AgglomerativeClustering import pandas as pd
import numpy as np
2. Создадим 20 точек данных в двумерном пространстве задачи:
dataset = pd.DataFrame({ |
|
|
|
|||||
|
'x': [11, 21, |
28, 17, |
29, 33, 24, |
45, 45, 52, 51, 52, 55, |
53, |
|||
55, |
61, |
62, |
70, |
72, 10], |
|
|
|
|
|
'y': [39, 36, |
30, 52, |
53, 46, 55, |
59, 63, 70, 66, 63, 58, |
23, |
|||
14, |
8, |
18, 7, 24, |
10] |
|
|
|
||
}) |
|
|
|
|
|
|
|
|
3.Создадим иерархический кластер, указав гиперпараметры. Используем функцию fit_predict для фактической работы алгоритма:
cluster = AgglomerativeClustering(n_clusters=2, affinity='euclidean', linkage='ward') cluster.fit_predict(dataset)
4.Теперь рассмотрим связь каждой точки данных с двумя созданными класте рами (рис. 6.12).
Рис. 6.12
Вы можете увидеть, что кластеры используются похожим образом как в ие рархических алгоритмах, так и в алгоритмах k-средних.
Оценка кластеров
Цель качественной кластеризации состоит в том, чтобы точки данных, принад лежащие отдельным кластерам, были дифференцируемыми. Это подразумева ет следующее:
zz Точки данных, принадлежащие к одному и тому же кластеру, должны быть как можно более похожими.
Алгоритмы кластеризации |
167 |
zzТочки данных, принадлежащие к отдельным кластерам, должны быть как можно более отличающимися.
Иногда пользователь может самостоятельно оценить результаты кластеризации благодаря визуализации кластеров. Однако для количественной оценки качества кластеров существуют математические методы, например анализ силуэта. С его помощью сравниваются плотность и разделение в кластерах, созданных с по мощью алгоритма k-средних. График силуэта отображает близость каждой точки в определенном кластере по отношению к другим точкам в соседних кластерах. Каждому кластеру присваивается коэффициент в диапазоне [–0, 1]. В табл. 6.2 показано, что означают числа в этом диапазоне.
Таблица 6.2
Диапазон |
Значение |
Описание |
|
|
|
0.71–1.0 |
Отлично |
Кластеризация методом k-средних привела к созда |
|
|
нию групп, которые достаточно отличимы друг от |
|
|
друга |
|
|
|
0.51–0.70 |
Приемлемо |
Кластеризация методом k-средних привела к созда |
|
|
нию групп, которые более или менее отличимы друг |
|
|
от друга |
|
|
|
0.26–0.50 |
Слабо |
Кластеризация методом k-средних привела к группи |
|
|
ровке, но на качество результата полагаться не стоит |
|
|
|
< 0.25 |
Кластериза |
С имеющимися данными и при выбранных параме |
|
ции не |
трах не удалось провести кластеризацию методом |
|
обнаружено |
k-средних |
|
|
|
Обратите внимание, что каждый кластер в пространстве задачи получает от дельную оценку.
Применение кластеризации
Кластеризация используется везде, где нужно обнаружить базовые закономер ности в наборах данных.
Кластеризация может использоваться, например, в следующих областях госу дарственного управления:
zz Анализ очагов преступности. zzСоциально-демографический анализ.
