Кортеж

Еще одна структура данных, которую можно использовать для хранения кол­ лекции, — кортеж. В отличие от списков, кортежи являются неизменяемыми (доступными только для чтения) структурами данных. Кортежи состоят из нескольких элементов, заключенных в круглые скобки ( ).

Кортежи, как и списки, могут включать в себя элементы разных типов, в том числе сложные типы данных — внутри кортежа может быть еще один кортеж. Таким образом, мы можем создавать вложенные структуры. Это особенно по­ лезно для работы с итеративными и рекурсивными алгоритмами.

В данном коде показано, как создавать кортежи:

>>>bin_colors=('Red','Green','Blue','Yellow')

>>>bin_colors[1]

'Green'

>>>bin_colors[2:]

('Blue', 'Yellow')

>>>bin_colors[:-1]

('Red', 'Green', 'Blue')

# Nested Tuple Data structure (вложенный кортеж)

>>>a = (1,2,(100,200,300),6)

>>>max(a[2])

300

>>> a[2][1]

200

Обратите внимание, что в представленном выше коде а[2] относится к третье­ му элементу, который является кортежем: (100,200,300); a[2][1] относится ко второму элементу внутри этого кортежа, который является числом 200.

По возможности старайтесь использовать неизменяемые структуры данных вместо изменяемых (например, кортежи вместо списков), так как это улучшит производительность. В особенности это касается обработки больших данных: неизменяемые структуры работают зна­ чительно быстрее, чем изменяемые. Мы платим определенную цену за возможность изменять элементы данных в списке. Нужно понять, действительно ли это необходимо или же можно использовать кортеж, что будет намного быстрее.

Временная сложность кортежей

Временную сложность различных функций кортежей можно обобщить с по­ мощью «O-большого» (табл. 2.2).

Таблица 2.2

Append() — это функция, которая добавляет элемент в конец уже существую­ щего кортежа. Ее сложность равна O(1).

Словарь

Хранение данных в виде пар «ключ — значение» особенно полезно при работе с распределенными алгоритмами. В Python коллекция пар «ключ — значение» хранится в виде структуры данных, называемой словарем. Чтобы создать сло­ варь, в качестве атрибута следует выбрать ключ, лучше всего подходящий для идентификации данных во время обработки. Значением ключа может быть элемент любого типа, например число или строка. В Python в качестве значе­ ний также используются сложные типы данных, например списки. Если ис­ пользовать в качестве значения ключа словарь, можно создавать вложенные словари.

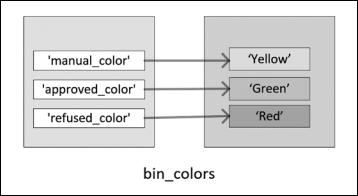
Чтобы создать простой словарь, который присваивает цвета различным пере­ менным, пары «ключ — значение» должны быть заключены в фигурные скобки { }. Например, следующий код создает простой словарь, состоящий из трех пар «ключ — значение»:

>>> bin_colors ={ "manual_color": "Yellow",

58 Глава 2. Структуры данных, используемые в алгоритмах

"approved_color": "Green", "refused_color": "Red"

}

>>> print(bin_colors)

{'manual_color': 'Yellow', 'approved_color': 'Green', 'refused_color': 'Red'}

Три пары «ключ — значение», созданные предыдущим фрагментом кода, также проиллюстрированы на рис. 2.2.

Рис. 2.2

Теперь давайте посмотрим, как получить и обновить значение, связанное с ключом.

1.Чтобы получить значение, связанное с ключом, можно использовать либо функцию get(), либо ключ в качестве индекса:

>>>bin_colors.get('approved_color')

'Green'

>>>bin_colors['approved_color']

'Green'

2.Чтобы обновить значение, связанное с ключом, используйте следующий код:

>>>bin_colors['approved_color']="Purple"

>>>print(bin_colors)

{'manual_color': 'Yellow', 'approved_color': 'Purple', 'refused_color': 'Red'}

Данный код показывает, как обновить значение, связанное с определенным ключом в словаре.

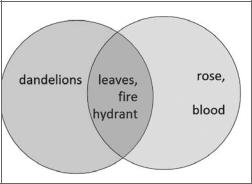
Обратите внимание, что некоторые вещи содержатся в обоих множествах. Эти два множества и их взаимосвязь можно представить с помощью диаграммы Венна (рис. 2.3).

Рис. 2.3 (dandelions — одуванчики, leaves — листья, fire hydrant — пожарный кран, rose — роза, blood — кровь)

Реализация этих множеств в Python выглядит следующим образом:

>>>yellow = {'dandelions', 'fire hydrant', 'leaves'}

>>>red = {'fire hydrant', 'blood', 'rose', 'leaves'}

Теперь рассмотрим код, который демонстрирует операции на множествах с ис­ пользованием Python:

>>> yellow|red

{'dandelions', 'fire hydrant', 'blood', 'rose', 'leaves'}

>>> yellow&red

{'fire hydrant'}

В данном примере продемонстрированы две операции: объединение и пересе­ чение. Объединение совмещает все элементы обоих множеств, а пересечение дает набор общих элементов для двух множеств. Обратите внимание:

zz yellow|red используется для объединения двух множеств;

zz yellow&red используется для получения пересечения yellow и red.

Анализ временной сложности множеств

В табл. 2.4 приведен анализ временной сложности для множеств.