сортировку списка за пару секунд. Таким образом, в случае большого объема входных данных имеет смысл приложить усилия: выполнить анализ произво­ дительности и выбрать алгоритм, который будет эффективно решать требуе­ мую задачу.

«О-большое»

«О-большое» используется для количественной оценки производительности алгоритмов по мере увеличения размера входных данных. Это одна из самых популярных методик, используемых для проведения анализа наихудшего сце­ нария. В этом разделе мы обсудим различные типы «О-большого».

Константная временная сложность (O(1))

Если выполнение алгоритма занимает одинаковое количество времени не­ зависимо от размера входных данных, то про него говорят, что он выполня­ ется постоянное время. Такая сложность обозначается как O(1). В качестве примера рассмотрим доступ к n-му элементу массива. Независимо от раз­ мера массива для получения результата потребуется одно и то же время. Например, следующая функция вернет первый элемент массива (ее сложность O(1)):

def getFirst(myList): return myList[0]

Выходные данные показаны ниже (рис. 1.7):

Рис. 1.7

zz Добавление нового элемента в стек с помощью push или удаление элемента из стека с помощью pop. Независимо от размера стека добавление или уда­ ление элемента займет одно и то же время.

zz Доступ к элементу хеш-таблицы.

zzБлочная (иначе называемая корзинная или карманная) сортировка (Bucket sort).

Линейная временная сложность (O(n))

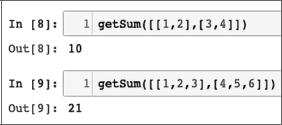
Считается, что алгоритм имеет линейную временную сложность, обознача­ емую O(n), если время выполнения прямо пропорционально размеру входных данных. Простой пример — добавление элементов в одномерную структуру данных:

def getSum(myList): sum = 0

for item in myList: sum = sum + item

return sum

Взгляните на основной цикл алгоритма. Число итераций в основном цикле линейно увеличивается с увеличением значения n, что приводит к сложности O(n) на рис. 1.8.

Рис. 1.8

Ниже приведены некоторые другие примеры операций с массивами:

zz Поиск элемента.

zz Нахождение минимального значения среди всех элементов массива.

Квадратичная временная сложность (O(n2))

Считается, что алгоритм выполняется за квадратичное время, если время вы­ полнения алгоритма пропорционально квадрату размера входных данных. На­ пример, простая функция, которая суммирует двумерный массив, выглядит следующим образом:

sum += item return sum

Обратите внимание на вложенный цикл внутри основного цикла. Этот вложен­ ный цикл и придает коду сложность O(n2) (рис. 1.9).

Рис. 1.9

Другим примером квадратичной временной сложности является алгоритм сор­ тировки пузырьком (представленный в главе 3).

Логарифмическая временная сложность (O(logn))

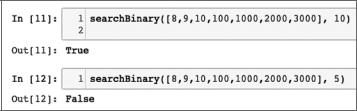
Считается, что алгоритм выполняется за логарифмическое время, если время выполнения алгоритма пропорционально логарифму размера входных данных. С каждой итерацией размер входных данных уменьшается в несколько раз. Примером логарифмической временной сложности является бинарный поиск. Алгоритм бинарного поиска используется для поиска определенного элемента в одномерной структуре данных, такой как список в Python. Элементы в струк­ туре данных должны быть отсортированы в порядке убывания. Алгоритм би­ нарного поиска реализован в функции с именем searchBinary следующим об­ разом:

def searchBinary(myList,item): first = 0

last = len(myList)-1 foundFlag = False

while( first<=last and not foundFlag): mid = (first + last)//2

if myList[mid] == item : foundFlag = True

else:

if item < myList[mid]: last = mid - 1

else:

first = mid + 1 return foundFlag

Работа основного цикла подразумевает тот факт, что список упорядочен. На каждой итерации список делится пополам, пока не будет получен результат (рис. 1.10):

Рис. 1.10

Определив функцию, мы переходим к поиску определенного элемента в стро­ ках 11 и 12. Алгоритм бинарного поиска более подробно обсуждается в гла­ ве 3.

Обратите внимание, что среди четырех последних представленных типов вре­ менной сложности O(n2) имеет худшую производительность, а O(logn) — луч­ шую. Фактически производительность O(logn) можно рассматривать как золо­ той стандарт производительности любого алгоритма (что, однако, не всегда достижимо). С другой стороны, O(n2) не так плох, как O(n3), но все же алгорит­ мы этого типа нельзя использовать для больших данных, поскольку временная сложность ограничивает объем данных, которые они способны обработать за разумное количество времени.

Чтобы понизить сложность алгоритма, мы можем пожертвовать точностью и использовать приближенный алгоритм.

Весь процесс оценки производительности алгоритмов носит итерационный характер, как показано на рис. 1.11.