Потенциальная энергия

Согласно формуле (1), при движении под действием консервативных сил совершаемая работа определяется разностью значений определенной величины, зависящей только от положения тела в пространстве. Назовем потенциальной энергией тела в однородном поле сил тяжести величину

W_п = mgh (2)

Тогда работа по перемещению тела из одной точки к другой будет равна:

A= –ΔW = – (W₂ – W₁) (3)

Во всех случаях по определению изменение потенциальной энергии, т.е. разность между конечным и начальным значением потенциальной энергии, равна взятой со знаком минус работе консервативных сил: ΔW = – A .

Потенциальная энергия может быть всегда изменена добавлением произвольной постоянной, так как физический смысл имеет только разность значений потенциальной энергии в двух точках. Это позволяет выбирать произвольным образом начало отсчета потенциальной энергии.

Кинетическая энергия

Функция, изменение которой равно работе всех сил, действующих на тело, называется кинетической энергией. В случае поступательного движения твердого тела

E_к = m·v²/2 (4)

Аналогичное утверждение справедливо также для системы тел.

Работа – мера изменения энергии. Обладая кинетической энергией, тело может совершить работу.

Свойства кинетической энергии:

• кинетическая энергия системы материальных точек равна сумме их кинетических энергий;

• кинетическая энергия – скалярная величина, являющаяся мерой механического движения системы.

Закон сохранения механической энергии

Работа, совершаемая консервативными силами, действующими на тело, равна, с одной стороны, изменению кинетической энергии тела, а с другой – взятому со знаком минус изменению потенциальной энергии E_п. Поэтому

E_2к – E_1к = – (E_2п – E_1п) (5)

или

E_1к + E_1п = E_2к + E_2п (6)

Таким образом, для отдельно взятого тела сумма кинетической и потенциальной энергии этого тела сохраняется в процессе движения.

Для консервативной системы справедлив закон сохранения механической энергии. Это означает, что при эволюции системы во времени энергия может переходить из одной формы в другую (кинетическая энергия – в потенциальную, и наоборот), но сумма этих двух величин не зависит от времени.

Если в замкнутой системе действуют силы трения, то энергия механического движения уменьшается, переходя в энергию теплового движения. В этом проявляется один из наиболее общих фундаментальных законов природы: энергия при всех изменениях форм движения материи остается постоянной.

Переход потенциальной энергии в кинетическую и наоборот можно проследить с помощью маятника Максвелла, в котором, кроме поступательного движения, происходит вращение диска относительно оси, проходящей через его центр. Поэтому в расчетах используется второй закон Ньютона для вращательного движения:

М = dL/dt = Jε (7)

где М – момент силы; L – кинетический момент (момент импульса) вращающегося тела; J – его момент инерции; ε – угловое ускорение.

Описание установки:

Данная установка, реализующая принцип маятника Максвелла,

предназначена для определения момента инерции тел вращения. Общий вид установки приведён на рис. 1.

На основании 1 закреплена стойка 2, к которой прикреплены неподвижный верхний кронштейн 3

и подвижный кронштейн 4. На верхнем кронштейне находится электромагнит 5, фотодатчик 6 и вороток с фиксатором 7 для закрепления и регулировки длины бифилярного маятника.

Нижний кронштейн 4 с фотодатчиком 8 можно перемещать вдоль стойки и фиксировать в выбранном положении. Маятник 9 – это диск, закрепленный на оси и подвешенный на бифилярном подвесе. На диск накладываются сменные металлические кольца 10, изменяющие момент инерции системы. Маятник с наложенным кольцом удерживается в верхнем положении электромагнитом 5. Длина маятника определяется по миллиметровой шкале стойки прибора. Сигналы с фотодатчиков служат для автоматического пуска и остановки миллисекундомера 11.Жестко соединенный с осью диск 9, подвешенный на двух нитях, предварительно намотанных на его ось, опускается под действием силы тяжести и приобретает вращательное движение за счет разматывающихся нитей. Нити в процессе движения разматываются до полной длины, а раскрутившийся диск продолжает вращательное движение в том же направлении, вследствие чего нити наматываются на ось, и диск поднимается вверх, замедляя при этом вращение и подъем. Дойдя до верхней точки, диск опять опускается вниз и т.д. При этом он будет совершать колебания вверх и вниз, почему устройство и называют маятником. На рисунке 2 показаны векторные величины, маятником. рисунке 2 показаны векторные величины, характеризующие движение маятника. Здесь: mg – сила тяготения;

T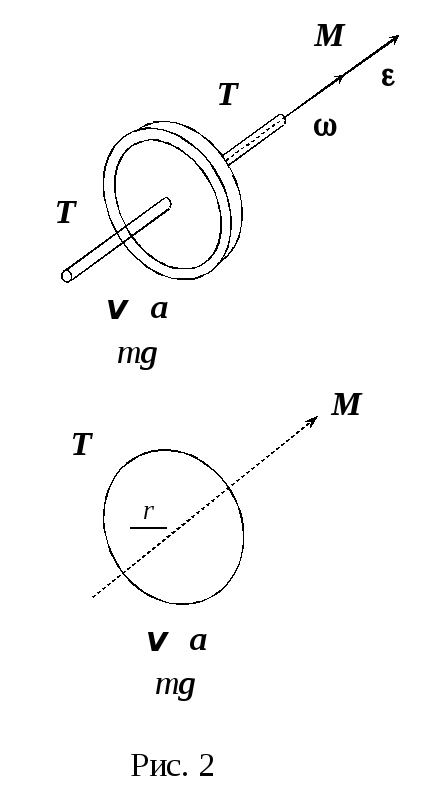 – сила натяжения одной нити;

v и a – линейные скорость и ускорение;

M – момент силы;

 и  – угловые скорость и ускорение;

r – скалярная величина, радиус валика. Величины M,  и  являются

псевдовекторами и направлены вдоль

оси вращения. При дальнейшем

рассмотрении, как и во введении,

вместо векторов

используются соответствующие

скаляры: g = | g |, v = |v |, ω = |  |

и т.д.,

что в данном случае оправдано.

Когда маятник поднят на высоту

h и неподвижен, его полная энергия равна

характеризующие движение маятника. Здесь: mg – сила тяготения;

T – сила натяжения одной нити; v и a – линейные скорость и ускорение;

M – момент силы;  и  – угловые скорость и ускорение;r – скалярная величина, радиус валика. Величины M,  и  являются псевдовекторами и направлены вдоль оси вращения. При дальнейшем рассмотрении, как и во введении, вместо векторов используются соответствующие скаляры:

g = | g |, v = |v |, ω = |  | и т.д., что в данном случае оправдано.

Когда маятник поднят на высоту h и неподвижен, его полная энергия равна потенциальной энергии, которая составляет E_п = mgh. В самом низком положении

(при h = 0): E_п = 0, и полная энергия маятника равна сумме кинетических энергий поступательного и вращательного движений:

E = E_k^пост + E_k^вр = mv²/2 + Jω²/2 (8)

По закону сохранения энергии полная энергия маятника в верхнем и нижнем положениях должна быть одинакова:

mgh = mv²/2 + Jω²/2 (9)