
математика
.pdf
Разложение функции f(x) в ряд Фурье принимает вид:
|
|
|
|
|
X |
ckei k¼l x: |
|
|
|
|
|
f(x) = |
1 |
(24) |
|
|
|
|
|
|
k=¡1 |
|
|
|
k¼ |
|
|
|
|
||
Функции |
ei |
|
x |
являются |
комплексными |
гармоническими |
|
l |
|||||||
функциями (см. формулу Эйлера). Коэффициенты ck образуют комплексный спектр функции f(x) (амплитуды комплексных гармонических
составляющих, |
образующих |
функцию |
f(x)). |
|
|
ИНТЕГРАЛ ФУРЬЕ
Интеграл Фурье получается предельным переходом из ряда Фурье при стремлении интервала разложения функции f(x) на всю числовую ось.
Для строгого вывода надо проверить допустимость предельного перехода, при этом накладываются определ¸нные ограничения на функцию f(x).
Чтобы оттенить практическую сущность интеграла Фурье, провед¸м вывод нестрого. Нужно помнить, что необходимым условием является существование присутствующих в формулах несобственных интегралов.
Подставляя (23) в (24), получим: члены ряда Фурье можно представить в виде,
X |
l |
k¼ |
|
k¼ |
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|||
f(x) = k=¡1 |
2l |
Z¡l f(»)ei |
l |
» d» ¢ ei |
l |
x = |
1 |
l |
k¼ |
k¼ ¼ |
||
|
|
|
|
|
|
1 |
||||||
|
|
|
|
|
|
X |
|
Z¡l f(»)ei l » d» ¢ ei l x ¢ |
|
|
||
|
|
|
|
|
= k=¡1 |
2¼ |
l |
: |
||||
Вводя переменную !, дискретные значения которой !k, а приращения d!k = ¼ , выражение в правой части этой формулы можно трактовать как интегральнуюl сумму для интеграла
l |
1 |
l |
|
Z¡l · |
Z¡l f(»)e¡i!» d»¸ei!x dx: |
||
|
|||
2¼ |
21

Переходя к пределу при l ! 1, получаем представление функции f(x) интегралом Фурье:
|
|
|
1 |
1 |
|
|
f(x) = |
1 |
Z |
Z |
f(»)e¡i!(x¡») d»dx |
(26) |
|
|
|
|||||
2¼ |
||||||
|
|
|
¡1 ¡1 |
|
|
|
Е¸ часто представляют в виду двух соотношений: преобразования
Фурье и обратного преобразования Фурье: |
|
||||
1 |
1 |
|
|||
F (!) = |
p |
|
|
Z¡1 f(x)e¡i!x dx; |
|
2¼ |
(27) |
||||
1 |
|
|
1 |
|
|
f(x) = p |
|
Z¡1 F (!)ei!x d!: |
|
||
2¼ |
|
||||
В отличие от ряда Фурье, имеющего дискретный спектр ck, спектр сигнала, выраженного с помощью интеграла Фурье является непрерывной функцией F (!).
22
Дифференциальные уравнения
Дифференциальным называется уравнение, в которое входит неизвестная функция и е¸ производные. Общий вид дифференциального уравнения порядка n:
F (x; y(x); y0(x); : : : ; y(n)(x)) = 0: |
(1) |
Здесь x– независимая переменная, y(x)– неизвестная |
функция, |
y(k)(x)– производная порядка k функции y(x). |
|
Удифференциального уравнения есть две особенности:
²Решениями дифференциального уравнения являются не числа, а функции,
²В уравнение, помимо неизвестной функции входят е¸ производные.
Порядком уравнения называется порядок старшей производной, входящей в уравнение. Уравнение (1) имеет порядок n.
В большинстве практических приложений дифференциальное уравнение имеет вид разрешенного относительно старшей производной:
y(n) = f(x; y; y0; : : : ; y(n¡1)): |
(2) |
В принципе, разрешая уравнение (1) относительно переменной y(n), его можно преобразовать в уравнение (2), хотя практически это не всегда удается выполнить в алгебраической форме.
Поскольку в практических задачах в подавляющем большинстве случаев встречаются уравнения, разрешенные относительно старшей производной, математиками разрабатывалась теория именно таких уравнений. Если в конкретной задаче получается дифференциальное уравнение не разрешенное относительно старшей производной, то его надо разрешить, а если это не удается сделать, придется разрабатывать специальные методы его исследования.
Дифференциальные уравнения, как правило имеют много решений. Для выбора из множества решений одного, кроме решаемого уравнения, удовлетворяются некоторые дополнительные условия: граничные, краевые и т.д.
Используются термины – частное и общее решение.
Частное решение – это какая-то конкретная функция y(x), обращающая дифференциальное уравнение в тождество.
23

Например, для уравнения y0 = y частным решением будет y = ex, а общим y = Cex. Если в общем решении положить C = 1, получим указанное частное решение. Общее решение – это функция y(x; C1; : : : Cn), зависящая не только от x, но и от других величин C1; : : : Cn, называемых произвольными постоянными, задавая значения которых можно получить любое частное решение.
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ПЕРВОГО ПОРЯДКА, ЗАДАЧА КОШИ, ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ РЕШЕНИЯ
Дифференциальное уравнение 1-го порядка, разрешенное относительно производной, имеет вид
y0 = f(x; y): |
(3) |
Дадим геометрическую интерпретацию решений уравнения (Рис.2). Пусть y = y(x) – частное решение уравнения (3). В любой точке плоскости Oxy, через которую проходит это решение, соотношение y0 = f(x; y) означает, что производная y0, то есть тангенс угла наклона кривой y(x), численно равен правой части системы – f(x; y(x)). Тангенс угла наклона, или вычисленный по нему угол наклона определяет направление, по которому будет двигаться решение из заданной точки при изменении
независимой переменной x.
Таким образом, уравнение (3) для каждой точки плоскости Oxy определяет направление, по которому движется изображающая точка (x; y(x)) решения y = y(x). Если это направление в каждой точке плоскости отметить отрезком прямой, исходящей из точки, решение будет представлять кривую, в каждой точке касающуюся исходящей из точки прямой.
На рисунке проведены построения для дифференциального уравне-
ния
y0 = ¡xy ;
решениями этого уравнения являются окружности с центром, находящимся в начале координат. В качестве примера, на рисунке также построено решение, соответствующее начальному условию y(3; 5)=0.
24

6 
















4 
















2 
















0 











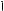




−2
−4
−6
−8 |
−6 |
−4 |
−2 |
0 |
2 |
4 |
6 |
8 |
Рис.2
Из такой геометрической интерпретации становится очевидным, что существует много решений дифференциального уравнения, поскольку можно указать много кривых, удовлетворяющих указанному условию. Через фиксированную точку плоскости (x0; y0), как правило, проходит только одно решение. Задача определения решения уравнения (3), проходящего через фиксированную точку, называется задачей с начальным условием или задачей Коши.
ТЕОРЕМА СУЩЕСТВОВАНИЯ И ЕДИНСТВЕННОСТИ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
В математике доказано целое семейство теорем, устанавливающих достаточные условия существования и единственности решения задачи Коши, в зависимости от свойств правой части дифференциального уравнения. Одна из таких теорем формулируется следующим образом:
Теорема.Если в уравнении y0 = f(x; y) функция f(x; y) и е¸ частная производная @f@y непрерывны в некоторой области D на плоскости Oxy,
содержащей некоторую точку (x0; y0), то существует единственное решение этого уравнения y = '(x), удовлетворяющее условию y = y0 при
x= x0.
Вбольшинстве практических приложений условия теоремы выпол-
няются. В тех случаях, когда условия теоремы не выполняются, может не существовать решения, проходящего через заданную точку, или через не¸ проходит несколько решений. Такие ситуации должны исследоваться специальными методами.
25
Выбирая различные точки (x0; y0), можно получить различные частные решения.
Если для фиксированного x0 обозначить y0 = C, где C – произвольная постоянная, то получится формула для общего решения y = '(x; C).
Очень часто в практических приложениях аргумент x представляет время. Исходя из таких ситуаций условие прохождения решения через данную точку называется начальным.
Иногда при получении общего решения его удается получить в виде неявной функции ©(x; y; C) = 0. Такая функция называется первым интегралом уравнения (3). Для дифференциального уравнения первого порядка такой интеграл один, у уравнений высокого порядка первых интегралов, в принципе, столько, каков порядок уравнения.
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ПОРЯДКА n
Для дифференциального уравнения порядка n
y(n) = f(x; y(1); y(2); : : : ; y(n¡1)) |
(4) |
также доказаны теоремы существования и единственности в разных предположениях относительно функции f. Из них вытекает, что при определ¸нных условиях существует и, притом, только одно решение, удовлетворяющее уравнению (4) и n начальным условиям: y(i)(x0)=yi0 i = 0; 1; : : : ; (n¡1).
С практической точки зрения это означает, что существует только одно решение уравнения(4), удовлетворяющее начальным условиям. Но если в отдельных точках условия теоремы существования и единственности нарушаются, необходимо дополнительно исследовать свойства решений и уравнение в целом в окрестности точек нарушения условий теоремы существования и единственности.
СИСТЕМА ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ 1-го ПОРЯДКА
В практических приложениях возникает необходимость одновременного исследования нескольких дифференциальных уравнений, образующих систему.
Набор n дифференциальных уравнений
y10 |
= f1(x; y1 : : : ; yn); |
y20 |
= f2(x; y1 : : : ; yn); |
. |
(5) |
. |
|
. |
|
yn0 |
= fn(x; y1 : : : ; yn); |
26
где yi – неизвестные функции независимой переменной x, представляет систему n дифференциальных уравнений 1-го порядка с n неизвестными.
Для такой системы доказана теорема существования и единственности, например, в таком варианте.
Теорема. Если функции fi; (i=1; : : : ; n) непрерывны по всем аргументам в замкнутой области D и имеют непрерывные и ограниченные частные производные по переменным y1; : : : ; yn, то существует одно, единственное решение системы (5)
y1(x) : : : yn(x);
определ¸нное в некоторой точке окрестности точки x0 и удовлетворяющее начальным условиям yi(x0) = yi0; (i = 1; : : : ; n).
Следствие. Переходя от точки x0 к другому значению x, находящемуся в найденной окрестности точки x0 и применяя теорему снова, можно продолжить найденное решение за пределы этой окрестности. Такое продолжение можно повторять многократно, распространяя, таким образом, найденное решение на всю или почти всю область D.
Существование и/или единственность решения может нарушиться в точках (n+1)-мерного пространства fx; y1; : : : ; yng, где условия теоремы существования и единственности нарушаются.
Таким образом, за исключением точек, в которых условия существования и единственности нарушаются, решения системы однозначно определяются начальными значениями неизвестных системы при x=x0. Обозначая эти значения постоянными величинами Ci, можно записать общее решение системы (5) в виде функций от независимой переменной x и n произвольных постоянных Ci:
yi = yi(x; C1; : : : ; Cn) i = 1; : : : ; n:
Общее решение системы (5) представляет набор n функций, каждая из которых зависит от независимой переменной x и n произвольных постоянных.
Частное решение, это единственное решение, которое получается из общего заданием конкретных значений произвольных постоянных.
На практике, когда уда¸тся решить систему (5) аналитически, вначале находится общее решение, а потом требуемое частное решение определяется из удовлетворения дополнительных, обычно начальных, условий.
Задача нахождения решения, удовлетворяющего начальным условиям, называется задачей Коши.
Аналитически уда¸тся найти решение дифференциальных уравнений только для отдельных классов систем. Разработаны численные методы
27
решения системы дифференциальных уравнений 1-го порядка. Они позволяют рассчитывать частные решения: для нахождения решений, удовлетворяющих другим начальным условиям нужно повторять расч¸ты заново.
СВЯЗЬ МЕЖДУ ДИФФЕРЕНЦИАЛЬНЫМИ УРАВНЕНИЯМИ И СИСТЕМАМИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Часто, для упрощения расч¸тов делается замена переменных в дифференциальных уравнениях.
Вчастности, дифференциальное уравнение порядка n можно преобразовать в систему дифференциальных уравнений, вводя новые переменные, равные производным исходной переменной.
Вдифференциальном уравнении (2)
y(n) = f(x; y; : : : ; y(n¡1))
введ¸м новые переменные:
y1 = y0; y2 = y00;
...
yn¡1 = y(n¡1):
Тогда, по определению новых переменных:
y0 = y1; |
|
y10 = y2 |
; |
. |
(6) |
. |
|
. |
|
y0n¡1 = f(x; y; y1; : : : ; yn¡1):
Система (6) есть система n дифференциальных уравнений первого порядка относительно переменных y; y1; : : : ; yn¡1, эквивалентных одному уравнению (2) порядка n.
Разобранная замена переменных представляет одну из возможных замен дифференциального уравнения высокого порядка системой дифференциальных уравнений. Можно придумать и другие.
Теоретически, систему дифференциальных уравнений можно эквивалентно заменить одним дифференциальным уравнением порядка n.
Для этого надо систему (4) трактовать как n алгебраических соотношений относительно неизвестных y1; y2; : : : ; yn и их производных.Процесс
28

сведения системы к одному уравнению заключается в получении явных выражений для переменных и производных из n ¡ 1 уравнений системы
(4) и подстановки их в оставшееся уравнение.
На практике, такой процесс часто затрудн¸н невозможностью получить явное алгебраическое выражение для отдельных переменных из уравнений системы, хотя теоретически эти переменные являются функциями остальных переменных.
Из изложенного следует важный вывод: одно дифференциальное уравнение порядка n теоретически эквивалентно системе n дифференциальных уравнений 1-го порядка или, например n=2 дифференциальных уравнений 2-го порядка (если n делится на 2) и так далее.
Общие решения дифференциального уравнения порядка n и системы n дифференциальных уравнений 1-го порядка зависят от n произвольных постоянных.
Рассмотрим классы и способы решения дифференциальных уравнений, которые можно решить аналитически. Начн¸м с дифференциальных уравнений 1-го порядка.
УРАВНЕНИЯ С РАЗДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ
Дифференциальное уравнение первого порядка y0 = f(x; y) называется уравнением с разделяющимися переменными, если функция f(x; y) представляет произведение функций, зависящих только от одной пере-
менной x и y: f(x; y) = f1(x) ¢ f2(y). Дифференциальное уравнение
dy |
= f1(x) ¢ f2(y) |
(7) |
dx |
решается следующим образом. Слева в равенстве стоит отношение дифференциалов, а справа – произведение функций, каждая из которых зависит от одной переменной. Очевидными алгебраическими преобразованиями это выражение приводится к виду, в котором слева будут члены, зависящие только от y, а справа – от x:
dy
f2(y) = f1(x) dx:
Полученное соотношение представляет условие равенства двух дифференциалов.
Если дифференциалы равны, то интегралы от дифференциалов отличаются на произвольную постоянную:
Z |
f2(y) = Z |
f1(x) dx + C: |
|
dy |
|
29

Это соотношение, при вычисленных интегралах, представляет первый интеграл уравнения (7).
Пример 11.Решим уравнение:
dxdy = xy :
Преобразуя его, получаем:
dyy = dxx :
Интегрируя это соотношение, получаем:
ln jyj = ln jxj + ln C:
Здесь для удобства последующих преобразований произвольная постоянная представлена в виде логарифма от произвольной постоянной.
Потенцируя полученное соотношение, получаем, что общее решение уравнения представляет множество прямых, проходящих через начало координат:
y = Cx:
Обратите внимание: решение, проходящее через начало координат не единственно. Объясняется это тем, что при x=0 условия теоремы существования и единственности (непрерывность и дифференцируемость правой части уравнения) не выполняются.
Замечание При выполнении алгебраических операций с дифференциальными уравнениями надо учитывать особенности операций с уравнениями. В частности, при делении уравнения на выражение, зависящее от переменных x и y можно потерять отдельные решения, соответствующие ситуации, когда делитель обращается в нуль.
Пример 12.Решим уравнение
|
|
|
|
|
y0 = |
y ¡ 1 |
: |
|
|
|||||||
|
|
|
xy |
|
|
|||||||||||
Разделяя переменные, получим: |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
y |
|
dy = |
1 |
dx; |
|||||||
|
|
|
|
|
y ¡ 1 |
|
|
|||||||||
а после интегрирования |
|
|
|
|
|
x |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
y |
|
|
|
1 |
|
|
|
|||||
|
|
Z |
|
|
dy = Z |
|
|
dx + C; |
||||||||
или |
|
y ¡ 1 |
x |
|||||||||||||
Z |
µ1 + y ¡ 1 |
¶dy = Z |
xdx + C; |
|||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
30
