Понятие о рекуррентных формулах
Иногда интегрирование по частям позволяет
получить соотношение между неопределенным
интегралом, содержащим степень некоторой
функции, и аналогичным интегралом, но
с меньшим показателем степени той же
функции. Подобные соотношения называются
рекуррентными формулами.
Выведем рекуррентную
формулу для интеграла
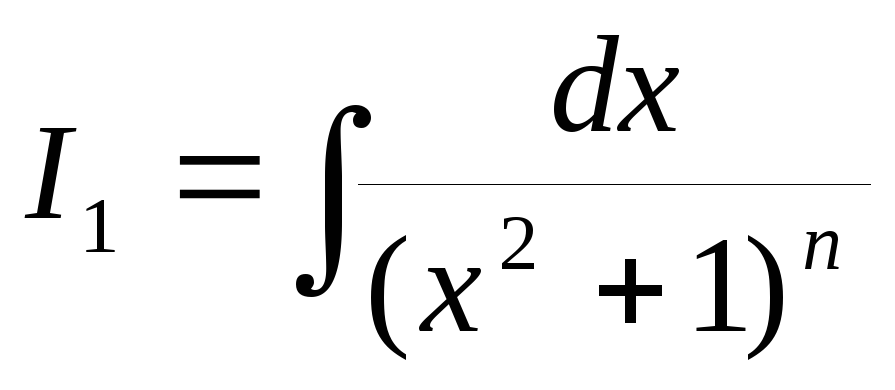 ,
гдеn
– целое положительное число.
,
гдеn
– целое положительное число.
При n=1
имеем табличный интеграл
 .
.
Пусть n1.
Представив единицу в числителе как
разность
 ,
получим
,
получим
 .
.
Во втором интеграле применим метод
интегрирования по частям:
 ,
, ,
, ,
, .
.
Тогда
 .
Следовательно,
.
Следовательно,
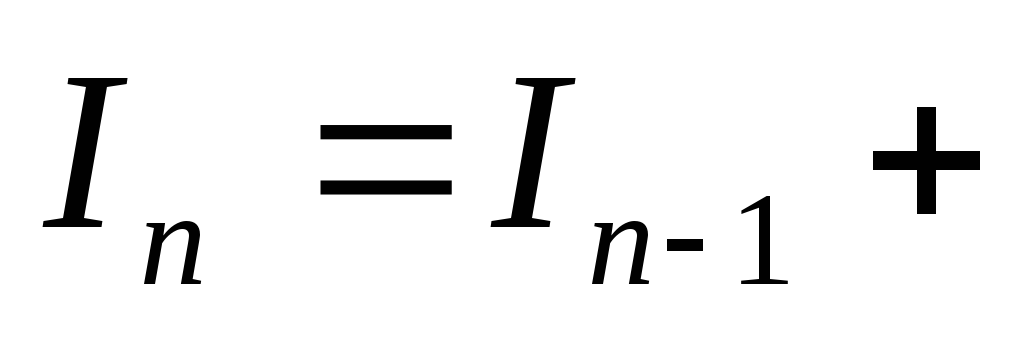
 ,
откуда
,
откуда
 .
.
Таким образом,
интеграл
 выражен через
выражен через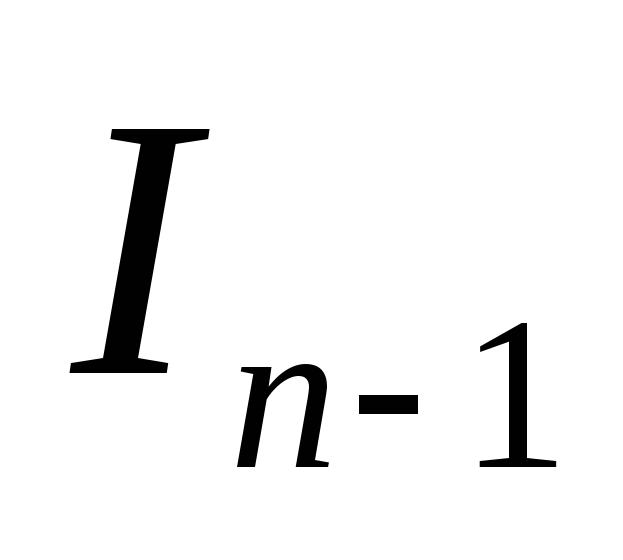 :
:
 (n1)
.
(n1)
.
Проверим нашу
готовность приступить к интегрированию
основных классов элементарных функций,
вычислив интеграл
 ,
последовательно применяя методы
непосредственного интегрирования,
подведения функции под знак дифференциала
и интегрирование по частям.
,
последовательно применяя методы
непосредственного интегрирования,
подведения функции под знак дифференциала
и интегрирование по частям.
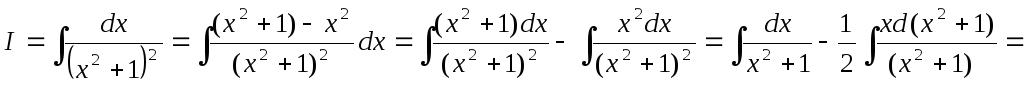

 .
.
Вычислим также интеграл
I=
Далее
полагаем u=eax
, dv=cosbxdx,
du=aeaxdx,
v= sinbx.
Следовательно
sinbx.
Следовательно
Получаем уравнение
относительно неизвестного интеграла
I. Решая его, находим
 или
или =
= .
.
Дифференциал функции сохраняет
одно и то же выражение независимо от
того, является ли ее аргументuнезависимой переменной или функцией
от независимой переменной. Это свойство
называется инвариантностью, т.е.
неизменностью формы дифференциала.
сохраняет
одно и то же выражение независимо от
того, является ли ее аргументuнезависимой переменной или функцией
от независимой переменной. Это свойство
называется инвариантностью, т.е.
неизменностью формы дифференциала.




 .
.