
- •Лекции по основам интегрального исчисления функций одной переменной и обыкновенным дифференциальным уравнениям
- •Неопределенный интеграл и его свойства
- •2. Основные свойства неопределенного интеграла
- •Свойство д) распространяется на случай алгебраической суммы любого конечного числа функций.
- •3. Таблица основных интегралов
- •В частности,
- •Основные методы интегрирования
- •1. Непосредственное интегрирование
- •2. Интегрирование методом замены переменной
- •3. Метод интегрирования по частям
- •Понятие о рекуррентных формулах
Основные методы интегрирования
1. Непосредственное интегрирование
Под непосредственным интегрированием понимают такой способ интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции и применения свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам.
Пример 1. Найти![]() .
.
Разделив числитель на знаменатель, получим:
![]() =
=![]() .
.
Отметим, что нет надобности после каждого слагаемого ставить произвольную постоянную, потому что их сумма есть также произвольная постоянная, которую мы пишем в конце.
Пример 2.Найти![]() .
.
Преобразуем подынтегральную функцию следующим образом:
 .
.
Применив табличный интеграл 1, получим:
 .
.
Пример 3.
![]() .
.
Пример 4.
![]() .
.
Пример 5.
![]()
=![]()
=![]() .
.
В некоторых случаях нахождение интегралов упрощается применением искусственных приемов.
Пример 6.Найти![]() .
.
Умножив подынтегральное выражение
на
![]() находим
находим
![]()
=![]() .
.
Пример 7.
![]() .
.
Пример 8.
![]() .
.
2. Интегрирование методом замены переменной
Вычислить заданный интеграл непосредственным интегрированием удается далеко не всегда, а иногда это связано с большими трудностями. В этих случаях применяют другие приемы. Одним из наиболее эффективных является метод замены переменной. Сущность его заключается в том, что путем введения новой переменной интегрирования удается свести заданный интеграл к новому, который сравнительно легко берется непосредственно. Существуют два варианта этого метода.
а) Метод подведения функции под знак дифференциала
По определению дифференциала функции
![]() .
.
Переход в этом равенстве слева направо
называют "подведением множителя
![]() под
знак дифференциала".
под
знак дифференциала".
Теорема об инвариантности формул интегрирования
Всякая формула интегрирования сохраняет свой вид при подстановке вместо независимой переменной любой дифференцируемой функции от нее, т.е., если
![]() , то и
, то и![]() ,
,
где
![]() - любая дифференцируемая функция отx.
Ее значения должны принадлежать
интервалу, в котором функция
- любая дифференцируемая функция отx.
Ее значения должны принадлежать
интервалу, в котором функция![]() определена и непрерывна.
определена и непрерывна.
Доказательство:
Из того, что
![]() ,
следует
,
следует![]() .
Возьмем теперь функцию
.
Возьмем теперь функцию![]() .
Для ее дифференциала в силу свойства
инвариантности формы первого дифференциала
функцииимеем
.
Для ее дифференциала в силу свойства
инвариантности формы первого дифференциала
функцииимеем
![]() .
.
Отсюда
![]() .
.
Пусть требуется вычислить интеграл
![]() .
Предположим, что существуют дифференцируемая
функция
.
Предположим, что существуют дифференцируемая
функция![]() и функция
и функция![]() такие, что подынтегральное выражение
такие, что подынтегральное выражение
![]() может быть записано в виде
может быть записано в виде
|
|
(1) |
Тогда
|
|
(2) |
т.е.
вычисление интеграла
![]() сводится к вычислению интеграла
сводится к вычислению интеграла![]() и последующей подстановке
и последующей подстановке![]() .
.
Пример
1. ![]() .
.
Пример
2.![]() .
.
Пример
3.![]() .
.
Пример
4.![]() .
.
Пример
5.![]() .
.
Пример
6.![]() .
.
Пример
7.![]() .
.
Пример
8.![]() .
.
Пример
9.![]() .
.
Пример
10.![]() .
.
Пример 11.
![]() .
.
Приведем далее примеры вычисления интегралов, которые нам понадобятся в теории интегрирования рациональных дробей.
Пример
12.НайтиI=![]() (0).
(0).
Представим подынтегральную функцию в виде:
![]() .
.
Следовательно,
I=![]()
=![]() .
.
Таким образом,
![]() .
.
Пример
12а. НайтиI=![]() ,
,
![]() .
.
Так как
![]() ,
,
следовательно
I=![]() .
.
Пример 13.Найти![]() (0).
(0).
Для
того, чтобы свести этот интеграл к
табличному, разделим числитель и
знаменатель подынтегрального выражения
на
![]() :
:
 .
.
Мы подвели постоянный множитель
![]() под знак дифференциала. Рассматривая
под знак дифференциала. Рассматривая![]() как новую переменную, получим:
как новую переменную, получим:
![]() .
.
Вычислим также интеграл, который имеет важное значение при интегрировании иррациональных функций.
Пример
14.НайтиI=![]() (ха,а0).
(ха,а0).
Имеем
 .
.
Итак,
![]()
![]() (ха,а0).
(ха,а0).
Представленные примеры иллюстрируют важность умения приводить данное
дифференциальное
выражение
![]() к виду
к виду![]() ,
где
,
где![]() есть некоторая функция отxиg– функция более простая для интегрирования,
чемf.
есть некоторая функция отxиg– функция более простая для интегрирования,
чемf.
В этих примерах были проведены преобразования дифференциала, такие как
![]()
![]()
![]() гдеb– постоянная
величина
гдеb– постоянная
величина
![]()
![]()
![]() ,
,
![]() ,
,
![]() ,
,
часто используемые при нахождении интегралов.
В таблице основных интегралов предполагалось, что xесть независимая переменная. Однако, эта таблица, как следует из изложенного выше, полностью сохраняет свое значение, если подxпонимать любую непрерывно дифференцируемую функцию от независимой переменной. Обобщим ряд формул таблицы основных интегралов.
3а.![]() .
.
4.![]() .
.
5.![]() =
=![]() .
.
6.![]()
![]() =
=
![]() .
.
7.![]() =
=
![]() .
.
8.
![]() (ха,а0).
(ха,а0).
9.
![]() (а0).
(а0).
Операция подведения функции
![]() под знак дифференциала эквивалентна
замене переменнойхна новую переменную
под знак дифференциала эквивалентна
замене переменнойхна новую переменную![]() .
Нижеследующие примеры иллюстрируют
это положение.
.
Нижеследующие примеры иллюстрируют
это положение.
Пример
15.НайтиI=![]() .
.
Произведем замену переменной по формуле
![]() ,
тогда
,
тогда![]() ,
т.е.
,
т.е.![]() иI=
иI= .
.
Заменив uего выражением![]() ,
окончательно получим
,
окончательно получим
I=![]() .
.
Выполненное преобразование эквивалентно
подведению под знак дифференциала
функции
![]() .
.
Пример 16.Найти![]() .
.
Положим
![]() ,
тогда
,
тогда![]() ,
откуда
,
откуда![]() .
Следовательно,
.
Следовательно,
![]() .
.
Пример 17.Найти![]() .
.
Пусть
![]() ,
тогда
,
тогда![]() ,
или
,
или![]() .
Следовательно,
.
Следовательно,
![]() .
.
В заключение отметим, что разные способы интегрирования одной и той же функции иногда приводят к функциям, различным по своему виду. Это кажущееся противоречие можно устранить, если показать, что разность между полученными функциями есть постоянная величина (см. теорему, доказанную на лекции 1).
Примеры:
а)
![]() .
.
![]() .
.
Результаты отличаются на постоянную величину, и, значит, оба ответа верны.
б) I=![]() .
.
![]() .
.

Легко убедиться, что любые из ответов отличаются друг от друга только на постоянную величину.
б) Метод подстановки (метод введения новой переменной)
Пусть интеграл
![]() (
(![]() - непрерывна) не может быть непосредственно
преобразован к виду табличного. Сделаем
подстановку
- непрерывна) не может быть непосредственно
преобразован к виду табличного. Сделаем
подстановку![]() ,
где
,
где![]() - функция, имеющая непрерывную производную.
Тогда
- функция, имеющая непрерывную производную.
Тогда![]() ,
,![]() и
и
![]() .
(3)
.
(3)
Формула (3) называется формулой замены переменной в неопределенном интеграле.
Как правильно выбрать подстановку? Это достигается практикой в интегрировании. Но можно установить ряд общих правил и некоторых приемов для частных случаев интегрирования.
Правило интегрирования способом подстановки состоит в следующем.
Определяют, к какому табличному интегралу приводится данный интеграл (предварительно преобразовав подынтегральное выражение, если нужно).
Определяют, какую часть подынтегральной функции заменить новой переменной, и записывают эту замену.
Находят дифференциалы обеих частей записи и выражают дифференциал старой переменной (или выражение, содержащее этот дифференциал) через дифференциал новой переменной.
Производят замену под интегралом.
Находят полученный интеграл.
Производят обратную замену, т.е. переходят к старой переменной.
Проиллюстрируем правило примерами.
Пример
18.Найти![]() .
.
Положим
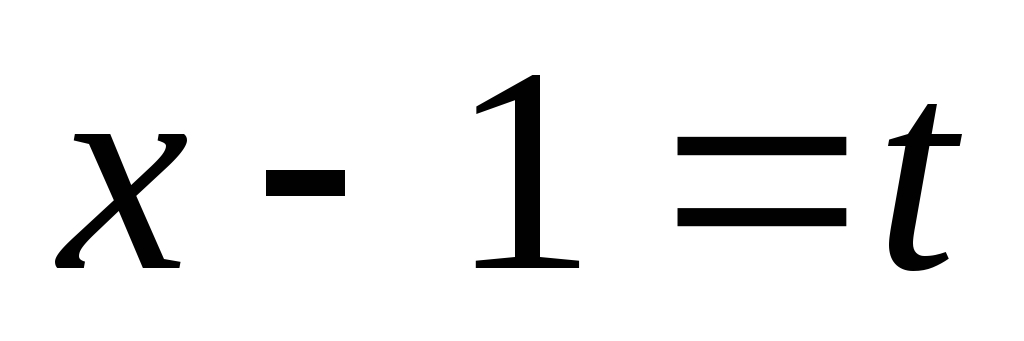 ,
тогда
,
тогда ,
,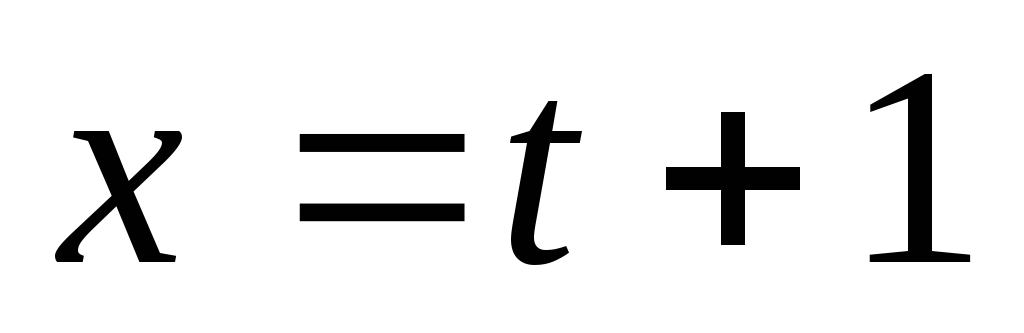 и
и
![]()
=
![]() .
.
Пример
19.Найти![]() .
.
Вычислим интеграл
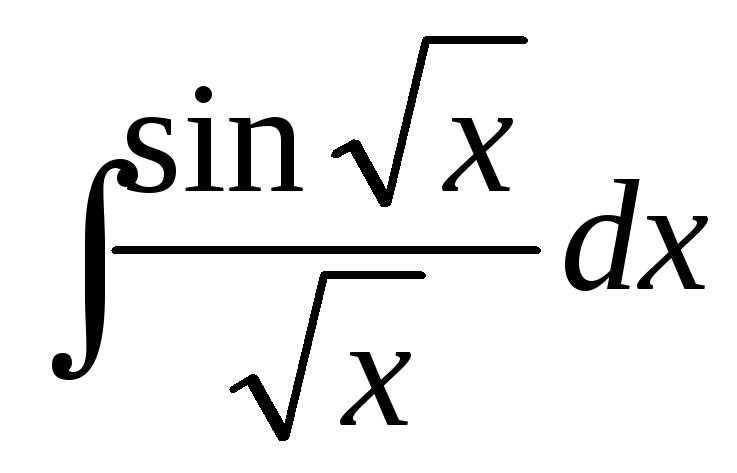 , придерживаясь следующей формы записи:
, придерживаясь следующей формы записи:
![]() =
= .
.
Этот интеграл найдем подведением
![]() под
знак дифференциала.
под
знак дифференциала.
![]() =
=![]() .
.
Пример 20.Найти![]() (
(![]() ).
).
Применим подстановку Эйлера:
 ,
где
,
где -
новая переменная.
-
новая переменная.
![]() ,
т.е.
,
т.е.![]() ,
или
,
или![]() .
Отсюда
.
Отсюда![]() ,
т.е.
,
т.е.![]() .
.
Таким образом, имеем
![]() .
Заменяя
.
Заменяя![]() его выражением черезx, окончательно
находим интеграл, играющий важную роль
в интегрировании иррациональных функций:
его выражением черезx, окончательно
находим интеграл, играющий важную роль
в интегрировании иррациональных функций:![]() (
(![]() ).
).
Студенты прозвали этот интеграл «длинным логарифмом».
Иногда вместо подстановки
![]() лучше выполнять замену переменной вида
лучше выполнять замену переменной вида![]() .
.
Пример 21.Найти![]() .
.
Полагая t=ex , получаем
 ,
, и
и
![]() .
.
Пример 22.Найти![]() .
.
Воспользуемся подстановкой
![]() .
Тогда
.
Тогда![]() ,
,![]() ,
,![]() .
.
Следовательно,
![]() .
.
В ряде случаев нахождение интеграла основывается на использовании методов непосредственного интегрирования и подведения функций под знак дифференциала одновременно (см. пример 12).
Проиллюстрируем этот комбинированный подход к вычислению интеграла, играющего важную роль при интегрировании тригонометрических функций.
Пример 23.Найти![]() .
.
Имеем

= .
.
Итак,
![]() .
.
Другой подход к вычислению этого интеграла:
 .
.
Пример 24.Найти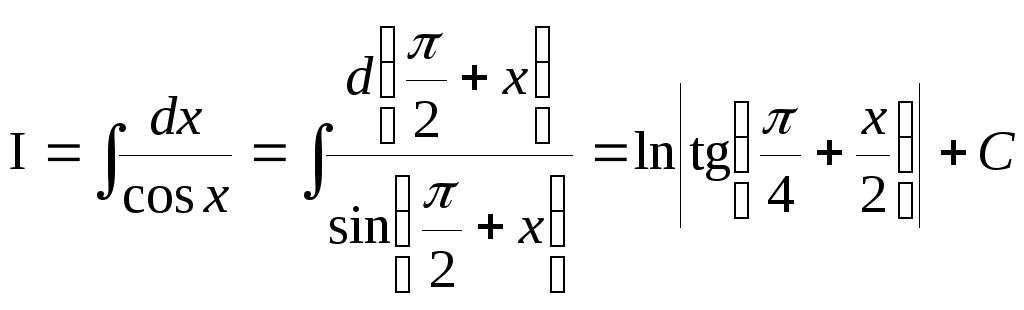 .
.
Заметим, что удачный выбор подстановки обычно представляет трудности. Для их преодоления необходимо овладеть техникой дифференцирования и хорошо знать табличные интегралы.
Лекция 3.
