
4. Интегралы вида .
Данные
интегралы рационализируются подстановкой
![]() .
Действительно, так как
.
Действительно, так как![]() и
и![]() ,
то
,
то![]() ,
гдеR(t)– рациональная функция отt.
,
гдеR(t)– рациональная функция отt.
Пример
31. Найти![]() .
.
Полагаем
![]() ,
,![]() .
Следовательно,
.
Следовательно,
![]()
Пример 21, представленный в лекции 2, также иллюстрирует способ рационализации интегралов рассмотренного вида.
Проанализированные методы и приемы интегрирования не исчерпывают всех классов аналитически интегрируемых элементарных функций.
Понятие об интегралах, не выражающихся через элементарные функции
Как было отмечено в § 1, если функция f(x) непрерывна на промежутке Х, то на этом промежутке существует функция F(x) такая, что F '(x) = f(x), т.е. существует первообразная для функции f(x).
В этом случае
говорят, что
![]() “берется”, выражается через элементарные
функции. Следует, однако, заметить, что
не всякая элементарная функция
“берется”, выражается через элементарные
функции. Следует, однако, заметить, что
не всякая элементарная функция
![]() имеет
в качестве своей первообразной
элементарную же функцию
имеет
в качестве своей первообразной
элементарную же функцию
![]() .
Если интеграл не выражается через
элементарные функции, то говорят, что
интеграл “не берется” или “его нельзя
найти”. Нельзя, например, взять интегралы
.
Если интеграл не выражается через
элементарные функции, то говорят, что
интеграл “не берется” или “его нельзя
найти”. Нельзя, например, взять интегралы
![]() ,
,![]() ,
,![]() ,
,![]() ,
так как не существуют элементарные
функции, производные от которых были
бы равны соответственно
,
так как не существуют элементарные
функции, производные от которых были
бы равны соответственно![]() ,
,![]() ,
,![]() ,
,![]() .
К числу “не берущихся” интегралов
относится интеграл Пуассона
.
К числу “не берущихся” интегралов
относится интеграл Пуассона![]() ,играющий
важную роль в теории вероятностей,
интегралы Френеля
,играющий
важную роль в теории вероятностей,
интегралы Френеля![]() ,
,![]() ,
интегральный логарифм
,
интегральный логарифм![]() ,
интегральные синус и косинус
,
интегральные синус и косинус![]() ,
,![]() ,
а также
,
а также![]() и
и![]() .
.
В заключение напомню известную истину, что никакая лекция, какой бы полной и понятной она Вам ни показалась, не может охватить круг рассматриваемых в ней вопросов в полном объеме. Необходимо работать самостоятельно над литературой, рекомендованной учебным планом. Но и ею не следует ограничиваться. Издается множество пособий, в которых Вы найдете для себя новое и поучительное. Именно так поступают наши отличники – «суперзвезды». Вот только один пример. Алеся Черняева (КШ–042) обратила мое внимание на так называемый «метод стрелок», который можно использовать при интегрировании по частям. Он изложен в книге «Сборник задач по высшей математике», которую написали К. Н. Лунгу, Д. Т. Письменный, С. Н. Федин (ему, как указано, принадлежит авторство этого метода) и Ю. А. Шевченко1
Привожу цитату из этой книги:
«Более наглядно и просто интегрирование по частям записывается с помощью эквивалентного метода стрелок

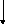

![]()
![]() '
'
![]()
![]()
т о
есть при интегрировании произведения
двух функций под каждой из них рисуется
стрелка, при этом на конце одной стрелки
(интегральной
о
есть при интегрировании произведения
двух функций под каждой из них рисуется
стрелка, при этом на конце одной стрелки
(интегральной![]() )
пишется
)
пишется
п ервообразная
соответствующей функции, а на конце
другой
ервообразная
соответствующей функции, а на конце
другой
( дифференциальной ' ) – производная второй функции; тогда в правой части
равенства получается произведение функции, стоящей на конце интегральной стрелки, на функцию в начале другой стрелки (эти функции соединены пунктиром в формуле) минус интеграл от произведения функций на концах стрелок. Или, более кратко, справа получается: конец интегральной стрелки на начало другой минус интеграл от произведения функций на концах стрелок».*
Ниже Алеся демонстрирует вычисление двух интегралов, основанных на этой методике.
Пример
1.Найти![]() .
.
![]()
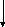


![]() '
'
![]()
![]()
![]()
Пример 2.Найти
![]()
![]()



'
![]()
2
![]()
![]()
Приложение
Из всего изложенного следует, что техника интегрирования сложнее по сравнению с дифференцированием. Необходимы определенные навыки, которые приобретаются на практике в результате решения большого числа примеров.
Ниже представлены образцы вычисления некоторых интегралов.
1.
![]()
![]()
2.
![]() .
.
3.

![]()
4.
![]()
5.
![]() .
.
6.
![]()
![]() .
.
7.
![]()
![]()
![]() .
.
8.

![]() .
.
9.
10.
![]()
![]() .
.
11.
![]()
![]() .
.
12.
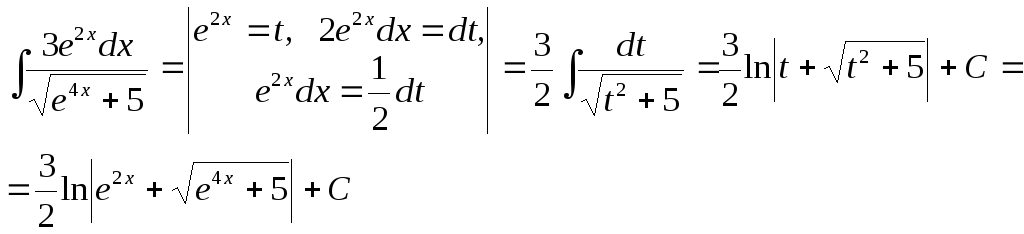 .
.
13.


![]()
![]() .
.
14.

![]() .
.
15.

 .
.
![]()
16.


 .
.
17.
![]() .
.
![]()
![]()
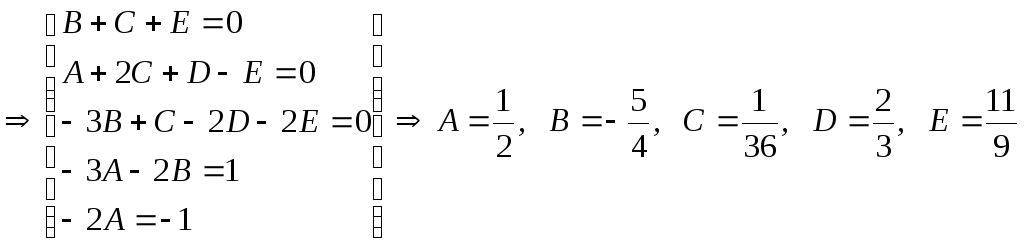 .
.
![]()
![]() .
.
18.
![]()
![]()
19.

![]() .
.
20.

![]() .
.
21.

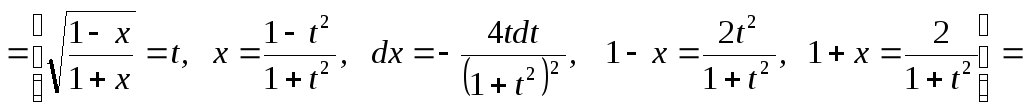
 .
.
22.

 .
.
I=

![]() (смотри
лекция 4, пример 8).
(смотри
лекция 4, пример 8).

24.
![]()

![]() .
.
25.
![]()
 .
.
26.
![]()
![]()
![]() .
.
27.
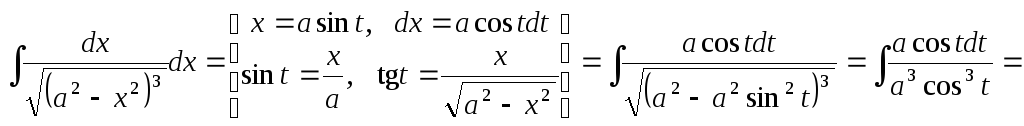
![]() .
.
28.
![]()

![]()
29.

![]()
![]()
![]()
![]() .
.
![]() .
.
1 Лунгу К. Н. и др. Сборник задач по высшей математике. – М: Пресс Рольф, 2001 г.
*Там же. – стр. 335.
