3. Интегрирование некоторых иррациональных функций

Рассмотрим ряд случаев, когда заменой переменной можно свести интегрирование иррациональных функций к интегрированию рациональных функций (т.е., как говорят, рационализировать интеграл).

Прежде всего отметим, что, если подынтегральное выражение содержит только линейную иррациональность то можно использовать подстановку.Так, например, если, то, полагая, имеем.

а) Интегралы вида , гдеn – натуральное число. Символ означает рациональную функцию отх и . Подстановка(n – общее наименьшее кратное показателей всех радикалов, под которыми х входит в подынтегральную функцию) сводит рассматриваемый интеграл к интегралу рациональной дроби.

Пример 23. Найти .

 Положим . Тогда.

Следовательно,

.

б) Интегралы вида , гдеа, b, с и d– постоянные числа,n–

натуральное число, аd – bс  0. Функцию виданазывают дробно-

линейной иррациональностью. Замена рационализирует интеграл. В самом деле,, откуда- рациональная функция отt. Далее,.

Поэтому:

где- рациональная функция отt.

Пример 24. Найти .

 Полагая , получим,.

Таким образом,

.

в) Интегралы вида путем выделения полного квадрата из квадратного трехчлена приводятся к рассмотренным выше интегралам (см. примеры 14 и 20 лекция 2).

Пример 25. .

Пример 26. .

г) При вычислении интегралов вида следует предварительно выделить в числителе производную квадратного трехчлена, стоящего под знаком корня , и разложить искомый интеграл на сумму двух интегралов:

Первый интеграл из полученных легко вычисляется при помощи подстановки и равен, а второй рассмотрен в пункте в).

Пример 27. Найти.

 Выделяя в числителе производную подкоренного выражения, получим:

.

д) Интегралы вида с помощью подстановки приводятся к рассмотренным в пункте в).

Пример 28. Найти.

 Полагаем , тогда. Следовательно,

.

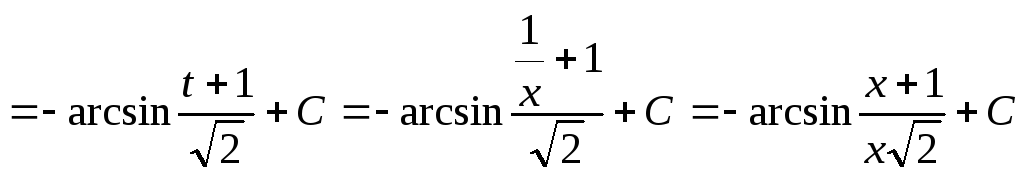е) Интегралы вида, гдеа, b, с– некоторые числа;0;R– рациональная функция отхи от. Функциюназывают квадратичной иррациональностью.

Если трехчлен имеет вещественные корних₁,х₂(х₁х₂) иа0, то

.

Следовательно, ,

т.е получаем интеграл, рассмотренный в пункте б).

Если х₁=х_2, то, т.е. под знаком интеграла находится

рациональная функция от х. Поэтому будем считать, чтоне имеет вещественных корней иа0. Тогда рационализация интеграла может быть достигнута с помощью подстановки Эйлера:

Отсюда, т.е.- рациональная функция отt.

Следовательно, - также рациональная функция отt.

Поэтому .

В качестве примера рассмотрим , вычисление которого представлено выше (см. лекция 3, пример 10) методом интегрирования по частям.

 Бином не имеет вещественных корней. Поэтому полагаем,,и,.

В силу этого

.

Учитывая, что , окончательно получаем:

.Ñ

Если в трехчлене ,а0, ас0, то для рационализации интеграла можно применить другую подстановку Эйлера:

.

Пример 29. Найти.

Трехчлен имеет комплексные корни иа0,с0, поэтому воспользуемся подстановкой. Возводя обе части равенства в квадрат, получаем:

, или.

Отсюда:

Таким образом,

.

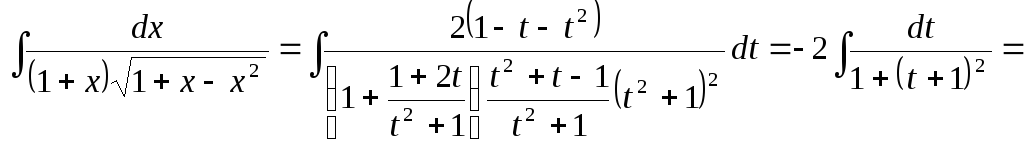
Следует отметить, что вычисление интегралов с помощью подстановки Эйлера обычно приводит к громоздким выражениям и трудоемким выкладкам, поэтому их следует применять, только если данный интеграл не удается вычислить более коротким способом.

Применим эйлерову подстановку к вычислению интеграла .

Имеем

.

Значит,.

Следовательно,

.

При вычислении интегралов рассматриваемого вида применяются также

искусственные приемы. Рассмотрим в качестве примера интеграл . Полагаяполучаем. Проводим следующую цепочку преобразований:

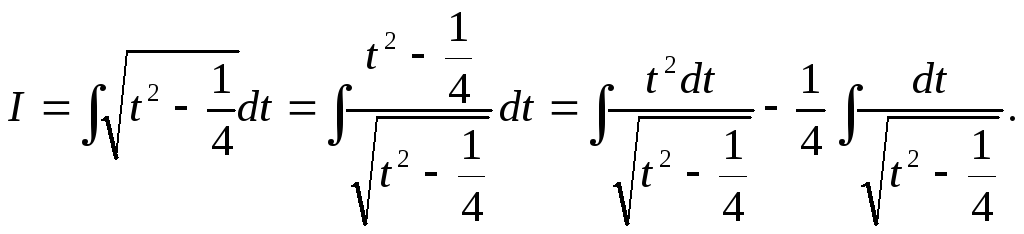
Вычислим интеграл .

Таким образом, имеем:

.

Возвращаясь к исходной переменной x,получаем

ж) Интегралы вида: 1., 2., 3.

приводятся к интегралам от рациональной относительно ифункции с помощью “тригонометрической подстановки”:

для интеграла 1: (или),dx=a costdt,,

для интеграла 2: (или),,

для интеграла 3: (или),.

Пример 30. Найти.

 Так как –2 х2, то, положивнайдем.

Следовательно,

.

Перейдем в полученном результате снова к переменной х. Имеем:

,,.

Так как ,, то

.

Таким образом,

.

Отметим, что рассмотренный интеграл можно вычислить и методом интегрирования по частям (см. лекция 3, пример 11).

“Острота зрения” должна подсказывать рациональный путь вычисления интегралов в тех случаях, когда вид подынтегральной функции “подталкивает” к применению кажущейся очевидной подстановки. Так, например, к интегралуне следует применять подстановку,так как .