Понятие о системах линейных дифференциальных уравнений с постоянными коэффициентами

Пусть мы имеем систему дифференциальных уравнений

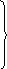
=a₁₁x₁ + a₁₂x₂ +…+a_1nx_n

=a₂₁x₁ + a₂₂x₂+…+a_2nx_n (11.7)

……………………………..…

=a_n1x₁ + a_n2x₂+…+a_nnx_{n. .}

Здесь t– аргумент,x₁(t),x₂(t),…x_n(t)- искомые функции,– постоянные. Система (11.7) называется системой линейных однородных дифференциальных уравнений с постоянными коэффициентами.

Эту систему можно решать путем сведения к одному уравнению n-ого порядка, которое в данном случае будет линейным. Но можно решать систему (11.7) и другим методом, не сводя к уравнениюn-ого порядка. Рассмотрим его на примере решения системы двух уравнений

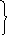
=a₁₁x₁+a₁₂x₂

=a₂₁x_{1 +} a₂₂x₂ (11.7а)

Будем искать частное решение системы в виде:

x1 = 1ekt, x2 = 2ekt.

(11.8)

Требуется определить постоянные ₁,₂иkтак, чтобы функции₁e^kt, ₂e^ktудовлетворяли системе уравнений (11.7а). Подставляя их в систему (11.7а), получаем:

k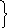₁e^kt = (a₁₁₁+a₁₂₂)e^kt

k₂e^kt= (a₂₁₁+a₂₂₂)e^kt

Сократим на e^kt. Перенося все члены в одну сторону и собирая коэффициенты при₁и₂, получим систему уравнений:

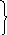(a₁₁- k) ₁ + a₁₂₂ = 0

(11.9)

a₂₁ ₁+ (a₂₂- k) ₂ = 0

Для того чтобы эта система имела нетривиальное (ненулевое) решение, необходимо и достаточно, чтобы её определитель был равен нулю:

a₁₁ –k a₁₂

=0 (11.10)

a₂₁ a₂₂ –k

Уравнение (11.10) называется характеристическим уравнением системы (11.9). Из уравнения (11.10) мы и получаем те значенияk, при которых система (11.9) имеет нетривиальные решения.

Ограничиваясь рассмотрением случая, когда корни характеристического уравнения (k₁иk₂) действительные и различные, на основе системы уравнений (11.9) находим

,

и

,.

Ее общим решением является система функций

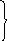
(11.11)

Пример 7.Решить систему уравнений,.

 Частные решения этой системы ищем в виде x₁= e^kt,x₂= e^kt(новые обозначения искомых постоянных ввели для удобства записи). Подставляя эти выражения в данную систему, для определенияи получим линейную однородную систему уравнений

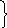(5−k)+2 = 0

(*)

−4+ (−1−k) = 0.

Составляем характеристическое уравнение:

5−k 2

=0

−4 −1−k

и находим его корни: k₁ = 1,k₂ = 3.

При k =k₁ = 1 система уравнений (*) эквивалентна уравнению 4 + 2 = 0, одно из решений которого есть =1, = −2. Поэтомуx₁⁽¹⁾ =e^t,x₂⁽¹⁾ = −2e^t являются решением исходной системы уравнений.

Подставив корень k = 3 в систему (*), получим эквивалентное ей уравнение 2 + 2 = 0. Одно из его решение есть = 1, = −1. Таким образом, найдено ещё одно решение исходной системы уравнений:x₁⁽²⁾ =e^3t,x₂⁽²⁾ = −e^3t.

Поскольку

e^t e^3t

= e^4t 0,

−2e^t −e^3t

найденные два решения являются линейно независимыми, а следовательно, образуют фундаментальную систему решений.

Поэтому общее решение исходной системы будет

x₁ =C₁e^t + C₂e^3t

x₂ = −2C₁e^t – C₂e^3t,

где С₁иС₂– произвольные постоянные.

Раздел «Дифференциальные уравнения» в программе курса математики на технологических факультетах обеспечивается лишь шестью лекциями. Поэтому важно в рамках самостоятельной работы углубит и расширить полученные знания, изучить как учебную литературу, так и специальные монографии, рекомендуемые преподавателями. Очень советую познакомиться, в частности, с замечательными книгами: А.М. Смойленко, С.А. Кривошея, Н.А. Перестюк. «Дифференциальные уравнения: примеры и задачи». «Высшая школа». 1989; В.В. Амелькин. «Дифференциальные уравнения в приложениях». «Наука». ГРФМЛ. 1987.

Важно получить представление о возмодностях использования дифференциальных уравнений при изучении реальных явлений и процессов, осознать широкое использование при их составлении геометрического и физического смысла производной, а также законов естественных наук. В качестве примеров полезно рассмотреть задачи о движении точки под действием постоянной и периодической силы, а также силы, пропорциональной скорости, о колебании точки под действием упругой силы, задачу о колебаниях математического маятника.

Наконец, необходимо с методами приближенных решений, с качественной теорией дифференциальных уравнений, одним из основных вопросов которой является проблема устойчивости решения или устойчивости движения.Этот вопрос исследован в работах выдающегося русского математика А.М. Ляпунрва (1857-1918).

Желаю Вам, мои юные друзья, успехов в учебе и прошу высказать критические замечания по содержанию представленного конспекта лекций. Это очень важно для мен в деле дальнейшего совершенствования учебного процесса.