Пример 4.Найти частное решение уравнения , удовлетворяющее начальным условиями.  Составляем характеристическое уравнение

и находим его корни: ,. Следовательно, общим решением является функция.

Дифференцируя общее решение, найдем

Постоянные инаходим из начальных условий:

Отсюда и. Итак, искомым частным решением является функция

.

Важным частным случаем решения (8.7) является случай, когда корни характеристического уравнения чисто мнимые. Это имеет место, когда в уравнении (7.1 ) , и оно имеет вид

.

(7.1а)

Характеристическое уравнение

,

(8.2а)

имеет корни .

Решение (8.7) принимает вид :

 (8.7а)

Пример 5. Общим решением уравнения, которому соответствует характеристическое уравнение с корнями,,

является функция .

 На основании изложенного получаем алгоритм решения линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами.

1. Записываем дифференциальное уравнение в виде (7.1): .

2. Составляем его характеристическое уравнение (8.2): .

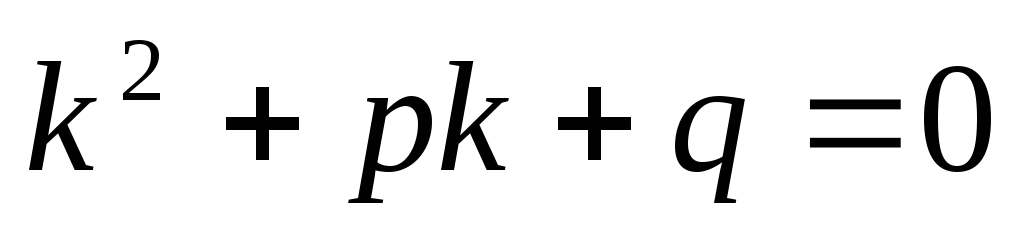3. Вычисляем дискриминант .

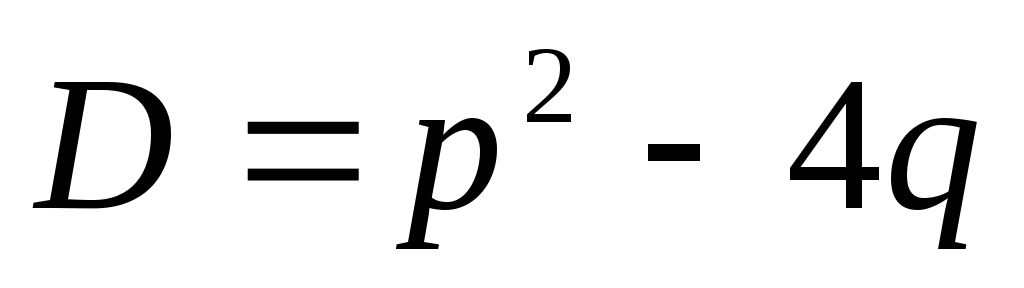а)Если0, то уравнение имеет два разных корняи, а общее решение записывается в виде (8.4):

б)Если=0, то уравнение имеет два равных корня, а общее решение записывается в виде (8.6):

.

в)Если0,то уравнение имеет комплексно сопряженные корни, а общее решение записывается в виде (8.7)

.

Для практического использования указанный алгоритм оформим в виде следующей таблицы :

Дифференциальное уравнение
Характеристическое уравнение
Дискриминант	0	=0	0
Корни характеристического уравнения
Множество Решений

9. Линейные неоднородные уравнения второго порядка с постоянными коэффициентами

Это уравнения вида

,

(9.1)

где и− данные постоянные числа, а(правая часть уравнения) − известная функция от. Структура общего решения такого уравнения определяется следующей теоремой.

Теорема. Общее решение неоднородного уравнения (9.1) равно сумме общего решениясоответствующего однородного уравнения

(9.2)

и частного решения () данного неоднородного уравнения.

Доказательство.Докажем, что сумма

(9.3)

есть общее решение уравнения (9.1). Сначала установим, что функция (9.3) является решением уравнения (9.1). Подставим в (9.1):

Так как есть решение уравнения (9.2), то выражение в первых скобках

тождественно равно нулю. Далее, так как есть решение уравнения (9.1), то выражение во вторых скобках равноТаким образом, в результате подстановки получаем тождество, и функция (9.3)- решение уравнения (9.1)

Докажем теперь, что выражение (9.3) есть общее решение уравнения(9.1), т.е. докажем, что входящие в него произвольные постоянные можно подобрать, чтобы удовлетворялись начальные условия, имеющие, как отмечалось выше, вид:

Учитывая, что

,

где и− линейно независимые решения уравнения (9.2),перепишем равенство (9.3) так:

.

Исходя из начальных условий, имеем

.

Здесь обозначают числовые значения рассматриваемых функций при.

Перепишем систему уравнений в виде

. (9.4)

Ее определителем является определитель Вронского для функций ив точке. Он отличен от нуля, так как эти функции по условию линейно независимы. Следовательно, существуют такие решенияисистемы (9.4), при которых формула (9.3) определяет решение уравнения (9.1), удовлетворяющее данным начальным условиям.

Теорема доказана.

Таким образом, чтобы найти общее решение линейного неоднородного уравнения, нужно найти общее решение соответствующего однородного уравнения (для этого используем результаты изложенного выше пункта 8) и какое-нибудь частное решение неоднородного уравнения. Вид частного решения уравнения (9.1) зависит от вида правой части этого уравнения.

Лекция 11.