Метод нахождения интегрируемых комбинаций

Сущность этого метода состоит в том, что с помощью арифметических операций из уравнений данной системы образуют так называемые интегрируемые комбинации,то есть легко интегрируемые уравнения относительно новой неизвестной функции.

Пример 1.Решить систему уравнений , .

 Складывая почленно эти уравнения, находим одну интегрируемую комбинацию:

, , , .

Почленно вычитая из первого уравнения системы второе, получаем другую:

, , ,

Из найденных уравнений определяем решение системы

, , или ,

где , .

Пример 2. Решить систему уравнений , .

 Замечаем, что при сложении уравнений системы в правой части пропадают неизвестные х и у. То же самое происходит при сложении уравнений с множителямихи у соответственно:

,

Или

dx +dy = -dt , xdx + ydy = −tdt.

Интегрируя эти равенства и перенося влево член с t, получим первые интегралы системы в виде:

x+ y +t =C₁, x²+ y² + t²=C₂.

Отсюда можно выразить х иу черезt,C₁,C₂.т.е. получить общее решение системы.

Геометрическая интерпретация. Эти интегралы в пространствезадают окружность как пересечение сферыx² + y² + t² =C₂ cплоскостьюx+ y +t =C₁ . Проектируя эту окружность на фазовую плоскость, получим на ней эллипс. Его уравнение находится исключениемtиз первых интегралов.

Пример 3. Решить систему уравнений , .

 Умножив обе части первого уравнения на у, а второго – нах и сложив почленно полученные уравнения, имеем

или .

Отсюда xу =C₁t _. (*)

Вводя (*) в первое уравнение системы, получим .

Интегрируя это уравнение, находим х:

, , .

Из равенства (*) в случае имеем .

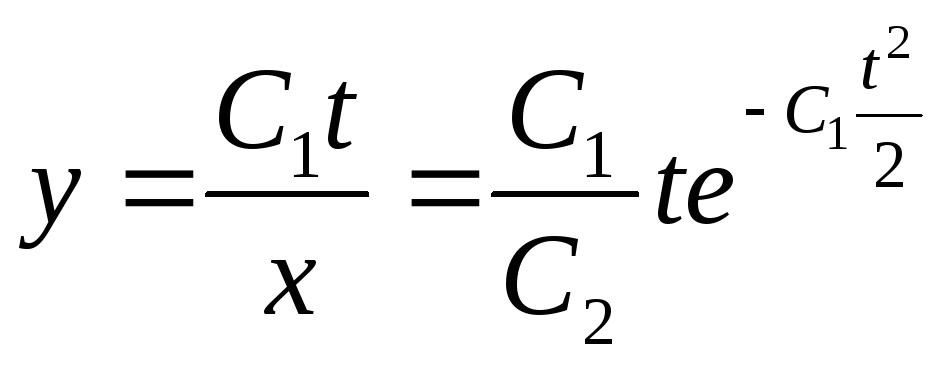Кроме того, если у = 0, из первого уравнения системых = С, а еслих = 0, то из второго уравненияу = Сt.

Метод исключения неизвестных

Иногда нормальную систему дифференциальных уравнений удаётся привести к одному уравнению более высокого порядка, содержащему одну неизвестную функцию. Общая схема приведения состоит в следующем. Дифференцируя, например, первое из уравнений (11.1) последовательно (n-1) раз и подставляя каждый раз вместо производныхих значения, из остальных уравнений этой же системы имеем

= F1 (t, x1, x2,…xn),
= F2 (t, x1, x2,…xn),
…….……………………	(11.5)
= Fn-1 (t, x1, x2,…xn),
= Fn (t, x1, x2,…xn).

Определив х_2, х₃, …х_nиз первых (n-1) уравнений системы (11.5) и подставив эти выражения в последнее уравнение системы, получим дифференциальное уравнениеn-ого прядка

=F.

(11.6)

Решив это уравнение, найдём решения исходной системы уравнений.

Пример 4.Решить систему уравнений,.

 Дифференцируя обе части первого из данных уравнений, имеем

. (**)

Из второго уравнения находим

.

Подставив это выражение в (**), получим уравнение второго порядка с постоянными коэффициентами:

.

Для его решения составим и решим характеристическое уравнение:

k² – 2ak +(1+a²) = 0, k_1,2 = a .

Следовательно, x = e^at(C₁ cos t + C₂ sin t). Из первого уравнения исходной системы определяемy(t):

y= − ax=ae^at (C₁ cos t + C₂ sin t)+ e^at (−C₁ sin t+ C₂ cos t) − ae^at (C₁ cos t + C₂ sin t)= =e^at (−C₁sin t + C₂ cos t). 

Пример 5.Решить систему уравнений,

 Дифференцируя второе уравнение: и учитывая, что, согласно первому, имеем. Отсюда.

Далее находим и подставляем во второе уравнение системы:

, где , .

Пример 6. Решить систему уравнений,

 Дифференцируя обе части первого из данных уравнений, имеем

. (***)

Из второго уравнения находим , поэтому уравнение (***) можно представить в виде.

Общее решение этого уравнения: . Из первого уравнения системы находим.
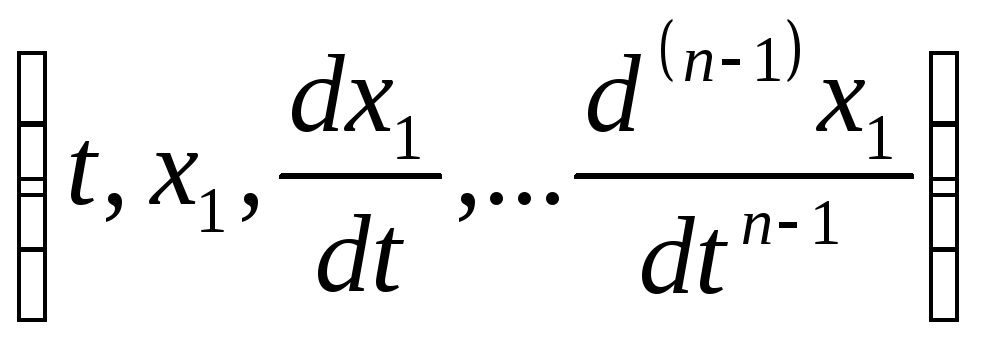