
TM_Lectures_part_I_10
.pdfЛекция 10 (ТМ, часть I)
Уравнение Мещерского
Сформулированный в Лекции № 9 ЗАКОН ИЗМЕНЕНИЯ И СОХРАНЕНИЯ ИМПУЛЬСА может использоваться для описания движения тел переменной массы.
Однако в случае рассмотрения движения относительно произвольно движущихся друг относительно друга систем отсчета, при переходе из одной системы отсчета в другую уравнения механики уже будут неэквивалентны!
Рассмотрим это подробно. Пусть мы имеем две системы отсчета: лабораторную (S, т.е. неподвижную) и систему отсчета S’ движущуюся относительно S произвольно.
Действительно полученные нами ранее уравнения механики были выведены в предположении, что масса движущихся тел не меняется.
Будем полагать, что масса тела может зависеть от времени:
m t
Масса тела может изменяться за счет:
-Присоединения новой массы из вне, например, при движении капли дождя сквозь облако. В этом масса капли может возрастать в результате столкновения с более мелких частиц воды.
-Потери массы, например, в результате расхода топлива машиной, самолетом и т.д.
Для описания такого движения будем использовать закон сохранения полного импульса механической системы.
|
|
̅ |
|
|
|
|
|
|
|
|
( ) ̅= |
|
|
, |
(1) |
|
|
|
|
|
|
|
|
|
|
|
|
||
̅= ( )̅( ). |
|
|
|
|
|
|
|||
|
|
|
|
|
|
m t |
|
t . |
|
Рассмотрим как изменяется масса и скорость тела от t : |
, v |
||||||||
|
|||||||||
Будем полагать, что в момент времени t t значение массы и скорости выражаются так:
( + ∆ ) m t m , |
(2) |
1
̅( + ∆ ) ̅( ) + ∆ ̅( ) . |
(3) |
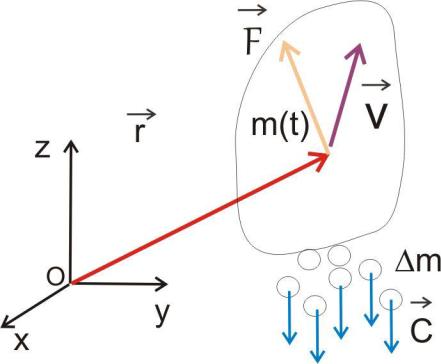
Будем полагать, что частицы новой массы налипают на/истекают из тела
относительноземли со скоростью c .
Схематически движение можно изобразить с помощью следующего рисунка:
Распишем закон изменения импульса в разностной форме через приращение импульса тела:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
P |
ext |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t 0 |
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Используя (2) и (3) приращение импульса можно записать так |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
m t m v |
t v |
m t v |
t mc |
m t v |
m v |
t c |
m v |
m t v |
m v |
t c |
||||||||
В результате левую часть уравнения (1) можно записать так |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
mr |
m v |
t c F |
ext |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь можно ввести обозначение |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
t . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c c |
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
Здесь c - скорость приходящей или уходящей от тела массы |
|
|
|
||||||||||||||||
относительно тела.
Тогда мы имеет следующий приближенный вид для уравнения (1)
2

|
|
|
|
ext |
|
|
|
||||
|
|
mc F |
|
||
|
mr |
|
|
||
. (4)
Как вы видите в правой части вместе с внешней силой в нем присутствует дополнительное слагаемое, содержащее производную от массы тела.
Это слагаемое именуют реактивной силой.
Это означает, что при отсутствии внешних сил, благодаря присоединения/истечения массы, тело может приобретать ускорение!
Полученное уравнение (4) называется уравнением реактивного движения или иначе, уравнением Мещерского.
Уравнение (4) содержит 4 неизвестные функции: три в составе ̅( ) и m(t).
Поскольку уравнение (4) представляет собой совокупность трех скалярных уравнений, относительно проекций ускорения на оси координат, это уравнение является неразрешимым.
Чтобы найти решение (4) необходимо использовать дополнительные
|
|
условия. При этом скорость c |
|
|
|
Эти условия могут быть заданы для
r
и
m t
.
В общем виде дополнительное условие записывается в следующем виде:
.
f t, r, m 0
В случае описании реактивного движения данная функция описывает либо расход топлива, либо время полета и так далее.
3
