TM_Lectures_part_I_02

Лекция 2 (ТМ, часть I)

Скорость и ускорение материальной точки в различных системах координат.

Скорость – первая производная радиус вектора по времени:

dr V

dt

Ускорение вторая производная по времени от радиуса вектора:

Вспомним запись радиус вектора в декартовой системе координат:

Соответственно в цилиндрической имеем следующее представление:

В сферической соответственно будет справедливо:

Так как базисные векторы ex, ey и ez постоянны (их производные по времени равны нулю) то скорость и ускорение будут иметь следующую форму записи через координаты:

Сформулируем задачу – найти общую форму записи скорости и ускорения в произвольной системе координат.

Введем в рассмотрение новое понятие.

Обобщенные координаты – это минимальный набор независимых величин, однозначно определяющих положение механической системы в пространстве.

Когда речь идет о системе материальных точек часто удобно использовать комбинированную систему координат.

Например, рассмотрим рисунок

1

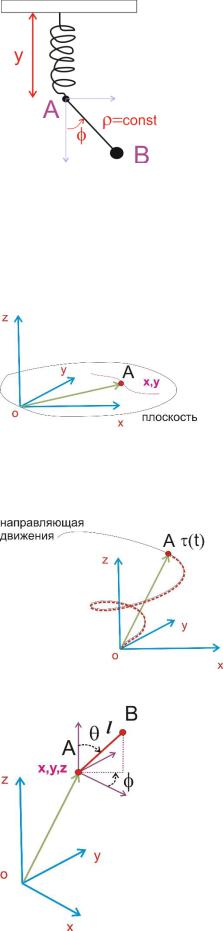
Положение т. А можно задавать в декартовой системе, в тоже время, положение т. В может быть задано в полярной системе с центром в т. А. В данном случае мы имеем две координаты y и .

Если нам точно известно о внутренних связях, т.е. некоторое ограничение на движение, то число координат может быть меньшим. Например, если материальная точка двигается в плоскости, то для его описания достаточно 2х координат x и y:

Если тело двигается по линии фиксированной формы (или некой кривой) то для определения положения тела достаточно одной координаты, в качестве которой можно выбрать длину пройденного пути (t).

Рассмотрим движение 2х точек А и B связанных стержнем (АВ)=l – фиксированная длины

Таким образом здесь можно использовать 5 координат: XА, YА, ZА, и .

2

В общем случае лучше перейти к более общему понятию – обобщенным координатам (они обозначаются q).

Рассмотрим, что это такое. Понятие об обобщенных координатах связано с понятиями о степенях свободы.

Степени свободы определяют количество независимых направлений, в которых может совершаться движение.

Рассмотрим, как перейти к обобщенным координатам в случае преобразования скорости

V xiei

Рассмотрим преобразование скорости в качестве первого шага дифференцирование по обобщенным координатам

rqi

Частная производная r по некоторой обобщенной координате задает в пространстве некоторое независимое направление . При этом

Н – длина вектора, задающего независимое направление в пространстве . Тогда мы можем ввести базис единых векторов.

Мы можем использовать декартовую систему координат, чтобы понять выражение (2).

Например, в случае перехода к Декартовым координатам имеем:

Используя формулу (2) и определение скорости, получим ее выражение в произвольной системе координат:

Формула (3) – общее выражение для V.

3

i 1

При этом Hi qi в (3) проекция V на соответствующую координатную ось.

Выполним вывод общей формулы для ускорения:

В случае цилиндрической системы координат для скорости имеем:

4