
- •Пояснительная записка
- •1 Постановка задачи
- •2 Теоретический материал
- •2.1 Двумерное преобразование Фурье
- •2.2 Алгебра кватернионов
- •2.3 Учет вещественности
- •3Описание разработанного алгоритма и программы
- •3.1 Описание работы программы
- •3.2 Описание разработанного алгоритма
- •4Тестирование программы
- •5Исследование алгоритма
- •Приложение а. Текст программы
Федеральное агентство по образованию
Государственное образовательное учреждение
высшего профессионального образования
«Самарский государственный аэрокосмический
университет имени академика С.П. Королева»
Кафедра геоинформатики
Пояснительная записка
к курсовому проекту по дисциплине
"Компьютерная алгебра"
Тема № 6
Cтудент: Валеев Д. Р. группа 657
Руководитель проекта: Чичева М. А.
Оценка: ____________
Дата: ____________
Самара 2010
ЗАДАНИЕ
Реализация и исследование быстрого алгоритма двумерного вещественного ДПФ с расщеплением основания с представлением данных в алгебре кватернионов.
ОГЛАВЛЕНИЕ
ЗАДАНИЕ 2
ОГЛАВЛЕНИЕ 3
1 Постановка задачи 4
2 Теоретический материал 5
Рис. 1. Заполнение недостающих областей на основании свойств симметрии 7
3 Описание разработанного алгоритма и программы 8
Рис. 2. Консоль приложения после запуска 8
Рис. 3. Пример работы программы 9
4 Тестирование программы 10
5 Исследование алгоритма 11
Таблица 1. Сравнение времени выполнения БПФ и ДПФ по формуле 11
Рис. 4. Сравнительные графики времени выполнения БПФ и ДПФ по формуле 11
Таблица 2. Сравнение времени выполнения БПФ с учетом и без учета 12
вещественности входного сигнала 12
Рис. 5. Сравнительные графики времени выполнения БПФ с учетом и 12
без учета вещественности входного сигнала 12
Приложение А. Текст программы 13
1 Постановка задачи
Нахождение спектра квадратной матрицы
размера
![]() с помощью быстрого алгоритма двумерного
вещественного ДПФ с расщеплением
основания с представлением данных в
алгебре кватернионов. Тестирование
полученной реализации алгоритма, ее
исследование и сравнение с «обычным»
алгоритмом двумерного ДПФ.
с помощью быстрого алгоритма двумерного
вещественного ДПФ с расщеплением
основания с представлением данных в
алгебре кватернионов. Тестирование
полученной реализации алгоритма, ее
исследование и сравнение с «обычным»
алгоритмом двумерного ДПФ.
2 Теоретический материал
2.1 Двумерное преобразование Фурье
Пусть
![]() - входной массив размераN×N.
Тогда его комплексный спектр Фурье
- входной массив размераN×N.
Тогда его комплексный спектр Фурье
![]() ,
,![]() , (1.1)
, (1.1)
где
![]() - комплексный корень из единицы степениN.
- комплексный корень из единицы степениN.
Под дискретным преобразованием Фурье со специальным представлением данных в рамках курсового проекта будем понимать преобразование вида
![]() . (1.2)
. (1.2)
Основная идея такого преобразования
заключается в погружении входного
сигнала и корней
![]() в четырехмерную алгебру кватернионов. При этом
корни
в четырехмерную алгебру кватернионов. При этом
корни![]() лежат в разных экземплярах поля
комплексных чисел, вложенных в,
у них разные мнимые единицы -iиj.
лежат в разных экземплярах поля
комплексных чисел, вложенных в,
у них разные мнимые единицы -iиj.
Отметим, что умножения на степени
![]() и
и![]() в соотношении (1.2) записаны слева и справа
от входного сигнала. Это сделано для
унификации записи. При использовании
алгебры кватернионовэто принципиально, так как умножение в
ней некоммутативно.
в соотношении (1.2) записаны слева и справа
от входного сигнала. Это сделано для
унификации записи. При использовании
алгебры кватернионовэто принципиально, так как умножение в
ней некоммутативно.
Поскольку элемент алгебры (кватернион![]() )
определяется набором четырех вещественных
чисел
)
определяется набором четырех вещественных
чисел![]() ,
то комплексный спектр (1) может быть
получен из спектра (2) в алгебреследующим образом:
,
то комплексный спектр (1) может быть
получен из спектра (2) в алгебреследующим образом:
![]() (1.3)
(1.3)
где
![]() – вектор компонент спектра,
– вектор компонент спектра,
 . (1.4)
. (1.4)
Таким образом, мультипликативная
сложность вычисления
![]() совпадает со сложностью вычисления
спектра в алгебре,
т.к. умножения на матрицыL,Iне
требуют выполнения нетривиальных
операций вещественного умножения.
совпадает со сложностью вычисления
спектра в алгебре,
т.к. умножения на матрицыL,Iне
требуют выполнения нетривиальных
операций вещественного умножения.
Рассмотрим алгоритм вычисления двумерного
ДПФ с расщеплением основания. Это –
схема декомпозиции двумерного спектра
(1.2), в которой ДПФ объема
![]() сводится к одной ДПФ
сводится к одной ДПФ![]() элементов входной последовательности
с четными индексами и двенадцати ДПФ
объемом
элементов входной последовательности
с четными индексами и двенадцати ДПФ
объемом![]() с элементами, имеющими хотя бы один
нечетный индекс. Пусть
с элементами, имеющими хотя бы один
нечетный индекс. Пусть
![]() ,
,
тогда
![]() (1.5)
(1.5)
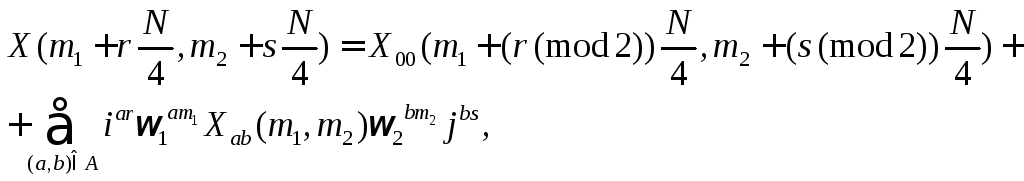 (1.6)
(1.6)
где
![]() размерность
ДПФ на текущем шаге.
размерность
ДПФ на текущем шаге.
