1.6. Режимы течения

Ламинарное (слоистое) – это упорядоченное течение жидкости без перемешивания соседних слоев, без пульсации скорости и давления. При таком течении в трубе постоянного сечения все линии тока параллельны её оси, однако возможно упорядоченное вихревое движение вокруг линий тока.

Турбулентное (бурное, возмущенное) – сопровождается интенсивным перемешиванием и пульсациями скорости и других параметров. Имеет место поперечное перемещение отдельных частиц жидкости и их вращение вокруг собственных осей.

В 1883 году Рейнольдс доказал существование двух качественно различных режимов течения в трубах. Переход от ламинарного к турбулентному режиму течения осуществляется внезапно, сопровождается усилением теплопередачи, увеличением потерь на трение. Из опытов при различных параметрах (μ, ρ, с, d) он установил для круглых труб, что этот переход определяется их комплексом и называется критическим числом Рейнольдса

зона 2200 ≤ Reêð ≤ 2500 , течение в которой называется переход-

ным.

С учетом ν = μρ и замены μ на ν получим самую простую формулу для расчета числа Рейнольдса

Re = c d .

ν

23

1.7.Динамический пограничный слой

Связкостью связано возникновение пограничного слоя при обтекании жидкостями твердых тел. Всю область течения жидкости около твердого тела можно разбить на две качественно отличные зоны:

1. Пограничный слой толщиной δ(х). Это относительно тонкий

слой δ⁄х≤1, примыкающий к поверхности твердого тела. В этом слое существенно изменяется скорость и ∂u/∂y>0. Поэтому только внутри пограничного слоя проявляется вязкость жидкости и ее необходимо учитывать в расчетах.

2. Набегающий невозмущенный поток и область, лежащая над пограничным слоем, в которых ∂u/∂y ≈ 0. Поэтому жидкость, текущая над пограничным слоем, можно считать идеальной (τ = 0) и анализировать ее движение по более простым законам движения идеальной жидкости. Пограничный слой возникает при всех реальных течениях в лопаточных машинах и двигателях и существенно влияет на их работу.

24

Глава 2. ГИДРОСТАТИКА

2.1.Абсолютное и относительное равновесие жидкости

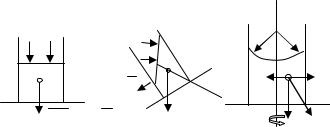
Вгидростатике изучаются закономерности, при которых жидкость находится в состоянии равновесия. Для гидростатики характерно постоянство формы и объема рассматриваемой жидкости и, как следствие, – отсутствие касательных напряжений. На элемент жидкости действуют только массовые силы, которые нормальны к поверхности. Общим условием равновесия жидкости или газа является равенство нулю равнодействующей всех сил и суммы всех моментов, приложенных к любому элементу жидкости, относительно любой оси. Различают абсолютное и относительное равновесие жидкости (см. рис. 2.1), при этом свободные поверхности имеют различный вид. Поверхность постоянного давления обладает следующими свойствами:

1. Две различные поверхности не пересекаются между собой.

Впротивном случае в точке пересечения было бы два значения давления;

2. Внешние массовые (объемные) силы, проекциями напряжения которых являются X, Y, Z, направлены по нормали в каждой точке поверхности постоянного давления.

Рис. 2.1. Абсолютное и относительное равновесие жидкости

На рис. 2.1 приведены примеры абсолютного равновесия (жидкость находится в сосуде только под действием силы тяжести) и относительного равновесия (сосуд движется равноускоренно

25

вниз по наклонной плоскости); жидкость вращается в цилиндрическом сосуде с постоянной угловой скоростью.

Свойства гидростатического давления в точке:

1.Гидростатическое давление есть давление сжатия, направленное по нормали к площадке.

2.Гидростатическое давление в точке жидкости не зависит от направления.

Согласно условиям равновесия сумма проекций всех сил на соответствующие оси координат, а также сумма проекций моментов этих сил относительно осей координат должна равняться нулю.

Выделим в жидкости элементарный объем в форме тетраэдра

сребрами dx, dy, dz соответственно расположенными на координатных осях Ox, Oy, Oz (рис. 2.2). На выделенный элемент жидкости действуют силы давления окружающей жидкости и массовые силы.

y dy dx Pz

Рис. 2.2. Элементарный объем

Силы давления на грани будут равны:

26

Так как нас интересует давление в точке, будем стягивать тетраэдр в точку.

px - pn = 0, py - pn = 0, pz - pn = 0; px = py = pz = pn = p = f(x, y, z).

Итак, гидростатическое давление в точке не зависит от направления, т.е. остается одинаковым по всем направлениям. Когда объем тетраэдра приближается к нулю, векторы силы приближаются к началу координат, а моменты сил относительно осей обращаются в нуль. В итоге второе условие равновесия автоматически выполняется. Очевидно, что для различных точек в жидкости величина гидростатического давления может быть различной, т.е. гидростатическое давление в точке является функцией только координат p = f(x, y, z).

2.2.Дифференциальное уравнение равновесия жидкости

вформе Эйлера

Рассмотрим условия равновесия частицы покоящейся жидкости или газа в объеме элементарного параллелепипеда с ребрами dx, dy, dz, соответственно параллельными координатным осям Ox, Oy, Oz. Будем считать, что находящаяся в равновесии частица жикости отвердела. Элементарный параллелепипед жидкости находится в равновесии под действием поверхностных и массовых (объемных) сил (рис. 2.3). Пусть px, py, pz – средние гидростатические давления на грани параллелепипеда, перпендикулярные со-

27