поверхность жидкости в баке - вытеснительная или баллонная подача; разности уровней жидкости - самотечная подача.
Методика гидравлического расчета трубопроводов одинаковая для всех видов подач.
Трубопроводы подразделяются на простые и сложные. Простые - постоянного сечения и без разветвлений; сложные – переменного сечения или(и) с разветвлениями.
При гидравлическом расчете трубопроводов используются уравнения неразрывности потока, Бернулли, формулы для расчета гидравлических сопротивлений, а также экспериментальные данные.
5.4.1. Простой трубопровод
Рассмотрим простой трубопровод, расположенный произвольным образом в пространстве, имеющий общую длину l, постоянный диаметр d, содержащий n местных гидравлических сопротивлений и передающий жидкость с параметрами ρ, ν.
Запишем уравнение Бернулли для участка 1-2 трубопровода при
условии Lмех = 0, с1 = с2 |
= с с учетом ρ L = |
p* |
+ p |
ò ð |
; |
||||||||
|
|
|
|
|
|
|
ã |
|
ì |
|
|
|
|
* |
= ξ ì |
|
ρc |
2 |
, |
pò ð |
= λò ð |
l |
|
ρc2 |
. |
|
|
|
|
|
|
|
|
||||||||
pì |
2 |
|
d |
2 |
|
||||||||
|
|
|
|
|
|||||||||
p1 |
− p2 |
= (z |
|
− z |
) + |
|
λ |
l |
|
|
2 |
|
|
||||
|
ρ |
1 |
|
|
d |
|||
|
|
|
|
|
|
|||
n |
|
|
c2 |
|
z + ξãΣ |
c |
2 |
, |
|
+ ∑ |
ξ ì i |
|
= |
|
|||||
2g |
2g |
||||||||
i=1 |
|
|
|
|
|
||||
|
|
l |
n |
|
где |
ξ гΣ = λ тр |
+ ∑ξ мi - суммарный коэффициент последова- |
||
d |
||||
|
|
i=1 |
тельно соединенных гидравлических сопротивлений трубопровода;
p1 − p2 = H - потребный напор, если он подлежит опреде-
ρ ï î ò ð
g
лению в результате расчета;
84
|
p1 − p2 |
= H |
ðàñï - располагаемый напор, в случае когда эта ве- |
|
|
||
|
ρ g |
|
|
личина задана. |
|
||
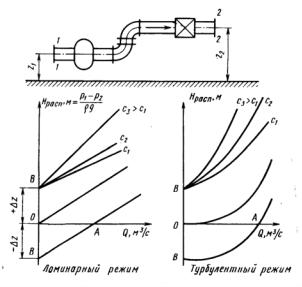
Рис. 5.9. Режимы течения в простых трубах
С учетом введенных обозначений, а также выражая скорость c через объемный расход Gv, можно получить характеристику трубопровода – зависимость потребного напора от расхода жидкости в виде
Hï î ò ð = ±Δz + CGvm ,
где m 1 – для ламинарных режимов течения жидкости; m 2 – для турбулентных режимов.
Чем больше гидравлическое сопротивление, тем больше величина с и тем круче характеристика H потр = f ( Gv ) .
Точка А на характеристике трубопровода (см. рис. 5.9) определяет объемный расход при движении жидкости самотеком за
85
счет разности нивелирных высот z2 - z1 < 0. В этом случае Нпот р= 0 и р1 = р2. Точка В соответствует покою жидкости и отрицательному потребному напору р1 > р2.
5.4.2. Сложные трубопроводы
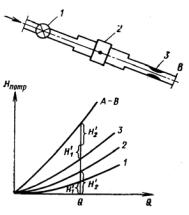
Последовательное соединение простых трубопроводов.
Рассмотрим последовательное соединение трех простых трубопроводов различного диаметра (см. рис. 5.10). В этом случае расход жидкости через все простые трубопроводы постоянен, а гидравлическое сопротивление всего трубопровода равно сумме гидравлических сопротивлений отдельных участков, т.е.:
Gv1 = Gv2 = Gv3 = Gv, |
ξãèäð Σ = ξãèäð1 = ξãèäð 2 = ξãèäð 3 . |
Рис. 5.10. Последовательное соединение трубопроводов
Запишем уравнение Бернулли для участка 1-2 в общем случае,
когда с2 ≠ с1: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
p |
2 |
|
|
c |
2 |
|
c2 |
|
c |
2 |
|
|
Hï î ò ð |
= z1 |
+ |
1 |
|
− z2 |
+ |
|
|
= |
|
2 |
− |
1 |
+ ξãΣ |
|
max |
, |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
ρ g |
|
|
ρ g |
|
2g 2g |
|
2g |
||||||||
где сmax - наибольшее значение скорости в сложном трубопроводе.
86
Для получения характеристики сложного трубопровода вначале построим характеристики трех простых трубопроводов. Характеристику сложного трубопровода получим, складывая все три потребных напора при одинаковых расходах. Далее гидравлический расчет сложного трубопровода производится по методике расчета простого трубопровода.
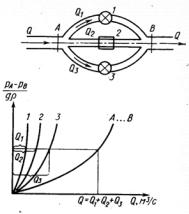
Рис. 5.11. Параллельное соединение трубопроводов
Параллельное соединение простых трубопроводов. Пусть в сечениях 1 и 2 соединяются параллельно три простых трубопровода различного сечения с n местными гидравлическими сопротивлениями (рис. 5.11). В этом случае расход жидкости через сложный трубопровод определяется как сумма расходов через три простые трубопровода: Gv = Gv1 + Gv2 + Gv3 .
Суммарные гидравлические потери всего сложного трубопровода равны гидравлическим потерям каждого простого трубопровода.
Характеристики отдельных трубопроводов можно представить в виде:
Hï î ò ð = c1Gvm11 ; H ï î ò ð = c2Gvm22 ; H ï î ò ð = c3Gvm33 .
Для построения характеристики сложного трубопровода с параллельным соединением простых трубопроводов необходимо
87