Расчёт гидравлических сопротивлений (потерь) различных устройств пневмо-гидравлических систем является одним из основных вопросов гидравлики.

5.1.Потери на трение (потери по длине)

Вчистом виде потери на трение можно наблюдать в прямом горизонтальном трубопроводе постоянного сечения (см. рис. 5.1). Эти потери обусловлены внутренним трением в жидкости, возрастают пропорционально длине трубопровода. Структура формулы для определения потерь на трение аналогична (5.1) и в метрах столба соответствующей жидкости имеет вид:

где ξтр – коэффициент гидравлических потерь на трение, с – сред-

нерасходное значение скорости, которое можно определить по формуле (5.2).

Коэффициент гидравлических потерь на трение удобнее представить в следующем виде:

где λтр – коэффициент сопротивления трению трубы длиной в один калибр, то есть трубы с l/d = 1.

Физический смысл коэффициента трения λтр найдём из ра-

венства нулю суммы двух сил, действующих на выделенный объём жидкости между сечениями 1 и 2:

где τ – напряжение трения на стенке трубы.

74

2

то есть λтр – величина, пропорциональная отношению напряжения

трения на стенке трубы к динамическому (скоростному) напору. Значение λтр сложным образом зависит от режима течения

(ламинарный, турбулентный), критерия Рейнольдса, относительной шероховатости стенки канала. Подробнее этот вопрос изложен в лабораторной работе № 4 (см. приложение А).

5.2. Местные гидравлические сопротивления

Этот вид потерь возникает за счёт местного изменения скорости, вихреобразования, связанного с местным отрывом потока от стенки канала или преграды на пути потока. Примеры наиболее распространённых местных гидравлических сопротивлений представлены на рис. 5.2-5.4. Структура формулы для расчёта местных гидравлических сопротивлений аналогична (5.1), в которой индекс г – «гидравлические» заменен на индекс м – «местные»:

pм = ξ м ρс22

Для большинства встречающихся в технике местных гидравлических сопротивлений значения ξ м определены теоретически

либо экспериментально и представлены в справочной литературе. Характерные сечения 1 и 2 до и после местного гидравлического сопротивления необходимо выбирать там, где параметры потока жидкости выровнялись. Важно отметить, что если площади характерных сечений у одного местного гидравлического сопротивления различны (см. канал с внезапным расширением на рис. 5.2), то в

75

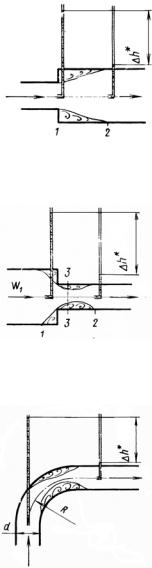
расчёте гидравлических потерь участвует меньшая площадь (диаметр), то есть в гидравлический расчет закладывается большее значение скорости.

Рис. 5.2. Расширение канала

Рис. 5.3. Сужение канала

Рис. 5.4. Поворот канала

76

5.3. Истечение жидкости из отверстий и насадков

Этот процесс реализуется при подаче топлива через форсунки

вкамерах сгорания авиационных, ракетных, автомобильных двигателей и других топливосжигающих установок; при подаче воды через сопла на лопасти гидротурбин, для получения реактивной тяги водомётных судов; при перетекании жидкости через жиклёры

всистемах регулирования двигателей.

Впроцессе истечения потенциальная энергия жидкости частично превращается в кинетическую энергию струи, а частично затрачивается на преодоление гидравлических сопротивлений.

Вобщем случае решение поставленной задачи состоит в определении скорости истечения жидкости; её расхода; гидравлических потерь при заданных условиях как в прямой, так и в обратной постановке.

5.3.1.Истечение жидкости через малое отверстие

втонкой стенке при постоянном напоре

На рис. 5.5 показана расчётная схема, применительно к которой сформулированы следующие основные и дополнительные условия.

Основные условия:

1.Сосуд неограниченной ёмкости (размеров).

2.Заданы свойства жидкости (плотность ρ, вязкость ν).

3.Истечение жидкости происходит в газообразную среду.

4.Отверстие находится под постоянным перепадом давления

(p1 + ρgz1 – p2 = сonst).

Дополнительные условия:

ρpg1 + z1

напор постоянным для любой его точки по высоте;

77

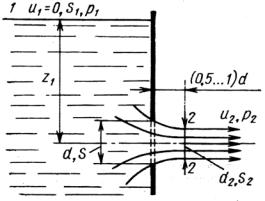
Рис. 5.5. Истечение жидкости

2.Стенка тонкая либо имеет острую кромку. В результате потери на трение по длине отверстия отсутствуют (ξтр = 0), несмотря на наличие местного гидравлического сопротивления (ξм > 0).

3.Отверстие достаточно удалено от свободной поверхности 1–1 и боковых стенок сосуда. В результате струйки жидкости подтекают к отверстию свободно, криволинейно и симметрично со всех сторон.

Требуется определить скорость истечения, расход жидкости и местное гидравлическое сопротивление отверстия в тонкой стенке.

Коэффициент сужения струи (ε). Траектории частиц жидко-

сти перед отверстием криволинейны. В результате возникают центробежные силы, направленные к оси отверстия, что приводит к сужению струи до своего минимального значения (d2 min) в характерном сечении 2–2, расположенном на расстоянии (0,5…1,0)d0 от отверстия. В сечении 2 давление в струе жидкости равно давлению газовой среды, в которую происходит истечение. Этот процесс оценивается коэффициентом сужения струи, представляющим собой отношение минимальной площади струи жидкости к площади отверстия через которое происходит истечение:

78

Коэффициент скорости (ϕ). Запишем уравнение Бернулли для участка 1–2. Исходя из основных и дополнительных условий: с1 = 0; с2 = const по сечению 2; нивелирная плоскость проходит через ось струи; Lмех = Lтр = 0. В результате

собой отношение реальной скорости истечения жидкости из отверстия к теоритическй.

Отличие коэффициента скорости от единицы связано с вязкостью жидкости и другими причинами, вызывающими неравномерность профиля скорости по высоте отверстия.

Коэффициент расхода (ψ). Расход жидкости через отверстие определяется по параметрам в сечении 2: G2 = ρ S2 c2.

Используя коэффициенты сужения струи (ε) и скорости (ϕ) этот расход записывается через площадь отверстия и идеальную скорость истечения: G2 = ρ ε S0 ϕ w2m.

Обозначим через коэффициент расхода ψ ψ = G2 - отноше-

G2 ò

ние фактического расхода к теоретическому. Учтем, что ψ = ε ϕ.

79