Энергетический смысл уравнения Бернулли для элементарной струйки идеальной жидкости заключается в постоянстве вдоль струйки полной удельной энергии. Уравнение Бернулли представляет собой закон сохранения механической энергии при установившемся движении идеальной жидкости.

Давление торможения. Запишем уравнение Бернулли для горизонтальной элементарной струйки (z1 = z2):

где р* – давление торможения; р – давление в потоке.

Из (4.16) следует важный практический вывод о том, что по измерениям р и р*, например, при помощи трубки Пито–Прандтля, можно определить локальную скорость жидкости или газа по следующей формуле

Подробнее см. лабораторные работы № 1 и 2 в Приложении А.

4.6. Уравнение Бернулли для элементарной струйки вязкой жидкости

Применим теперь закон сохранения энергии к элементарной струйке реальной (вязкой) жидкости. Допустим, что жидкость несжимаемая и теплообмен выделенной струйки с окружающей средой отсутствует. Движение жидкости установившееся. Выделим в движущейся жидкости элементарную струйку, ограниченную сечениями 1–1 и 2–2. При движении идеальной жидкости от сечения 1 к сечению 2 полная удельная механическая энергия является величиной постоянной:

67

Рис. 4.6. Схема замера давлений

При движении вязкой жидкости полная удельная механическая энергия не остается постоянной вдоль струйки: в первом сечении она больше, чем во втором, т.е. H10 > H20 . Запас полной энергии уменьшился, так как часть ее затрачена на преодоление сил трения:

H1 – H2 = hтр, в свою очередь hтр = Lтр/dm, где Lтр – работа сил трения. Энергия потока, израсходованная на преодоление сил трения, превращается в тепловую энергию, рассеивается и не может быть полностью восстановлена в механическую энергию в результате необратимости процесса. В этом смысле израсходованная на преодоление сил трения энергия называется потерянной. Тогда уравнение Бернулли для элементарной струйки вязкой несжимаемой жидкости примет вид:

где hтр – удельная энергия, потерянная на преодоление трения (напор). Таким образом, при установившемся движении вязкой несжимаемой жидкости без теплообмена с окружающей средой раз-

68

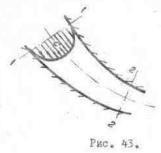
ность полных напоров в двух сечениях одной и той же струйки равна напору, потерянному на трение между этими сечениями. Линия полного напора располагается не в горизонтальной плоскости, а снижается в направлении течения. Чем больше наклон этой линии, тем интенсивнее потери на трение в струйке между сечениями 1 и 2. В потоке реальной жидкости, кроме сопротивления трения, существуют и другие сопротивления, так называемые местные сопротивления, например, сопротивление при внезапном сужении и расширении потока, при резком изменении направления скорости и др., на преодоление которых, естественно, также затрачивается часть напора жидкости. В этом случае уравнение Бернулли записывается в виде

где ∑h – суммарная потерянная энергия на преодоление всех со-

противлений, имеющих место между сечениями 1–2.

Рис. 4.7. Эпюра скорости

Вывод уравнения Бернулли для несжимаемой вязкой жидкости можно получить путем интегрирования уравнений движения в форме Навье–Стокса. Уравнение Бернулли, составленное для элементарной струйки, можно распространить на поток с поперечным

69

сечением конечных размеров, но при этом необходимо учесть неравномерность распределения скоростей по сечению вследствие вязкости жидкости. При движении вязкой жидкости вдоль твердой стенки, например в трубе, происходит неравномерное торможение потока в сечении под влиянием вязкости и сил молекулярного сцепления между жидкостью и стенками (у стенки торможение потока максимальное). Поэтому наибольшей величины скорость достигает в центральной части потока, а по мере приближения к стенке уменьшается практически до нуля. Получается распределение скорости в сечении. В неравномерном потоке имеет место сдвиг одних слоев жидкости относительно других, вследствие чего возникают касательные напряжения трения. Кроме того, движение вязкой жидкости сопровождается вращением частиц, вихреобразованием и перемешиванием. Для того чтобы одномерные уравнения элементарной струйки было можно применить к неравномерным потокам,

вводится понятие средней скорости. Кинетическая энергияÅêñð ,

вычисленная по средней скорости, не равна, а всегда меньше действительной величины кинетической энергии неравномерного потока Eк.

70

сти (коэффициен Кориолиса). Он представляет собой отношение действительной кинетической энергии потока к кинетической энергии потока с тем же расходом, но имеющего равномерное поле скоростей в том же сечении.

Таким образом, в уравнении Бернулли применительно к неравномерному потоку, слагаемое кинетической энергии должно

быта записано в виде α cñð2 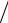2g . Для ламинарного движения α = 2,

для турбулентного α = 1,02÷1,04. В большинстве практических задач движение турбулентное, и принимают α = 1. Допустим, что в поперечных сечениях неравномерного потока гидростатический напор остается постоянным для всех точек данного сечения:

p + z = const . Тем самым предполагается, что при движении

ρ g

жидкости отдельные струйки, в поперечном направлении, оказывают друг на друга такое же давление, как слои жидкости в неподвижном состоянии. В действительности это имеет место только в параллельно-струйных потоках, а в остальных случаях это условие приближенно.

С учетом сказанного уравнение Бернулли для неравномерного потока вязкой несжимаемой жидкости будет иметь вид:

где cср – средняя по сечению скорость (обычно индекс «ср» опускается), не реально существующая, а условная скорость;

71

∑h – суммарная потеря удельной энергии (напора) на пре-

одоление различных гидравлических сопротивлений на участке между рассматриваемыми сечениями;

α − безразмерный коэффициент, учитывающий неравномерность распределения скоростей.

72

Глава 5. ГИДРАВЛИЧЕСКИЕ ПОТЕРИ. ИСТЕЧЕНИЕ ЖИДКОСТИ ИЗ ОТВЕРСТИЙ И НАСАДКОВ

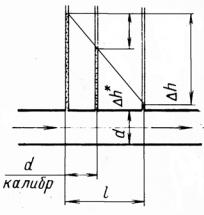
Гидравлические потери это потери удельной энергии (напора). Они зависят от шероховатости, формы и размеров канала, а также от скорости течения и вязкости жидкости и практически не зависят от абсолютного давления в жидкости. Опытами установлено, что гидравлические потери pг пропорциональны кинетической энергии потока и определяются формулой Вейсбаха:

где ξ2 – коэффициент гидравлических потерь. Он характеризует отношение потерянного к скоростному напору.

Рис. 5.1. Гидравлические потери

Гидравлические потери подразделяются на потери на трение

(потери по длине) и местные гидравлические потери.

При течении несжимаемой жидкости в каналах постоянного сечения S = сonst, несмотря на наличие гидравлических сопротивлений и связанного с этим потерь напора, сохраняется постоянным значение среднерасходной скорости по длине трубы:

73