Уравнения движения, записанные в такой форме (4.3), называются уравнениями Навье–Стокса для вязкой несжимаемой жидкости. Если при изучении движения вязкой жидкости одновременно учитывать и сжимаемость, то уравнения движения будут более сложными.

При движении вязкой (реальной) жидкости за гидростатическое давление в точке принимают среднее арифметическое значение давлений по трем произвольным, проходящим через данную точку, взаимно перпендикулярным площадкам, т.е.

ð = ðx + ðy + ðz .

3

Все слагаемые в уравнениях Навье-Стокса, так же как и в уравнениях Эйлера, имеют размерность ускорения. В левую часть уравнений входит проекция полного ускорения частицы, в правую часть − проекции ускорения от объемных сил, от сил давления и от сил вязкости (трения). Неизвестными величинами являются скорости cx, cy, cz, давление р и в общем случае течения сжимаемой жидкости плотность ρ. Зависимость μ от температуры считается известной. Для того чтобы получилась замкнутая система уравнений, в которой число уравнений равнялось числу неизвестных, необходимо к уравнениям Навье–Стокса присоединить уравнение неразрывности движения

а в случае сжимаемой жидкости еще и характеристическое уравнение

ρ = f(p, T).

4.3. Уравнение количества движения

При решении некоторых задач МЖГ используется уравнение количества движения. Важнейшей особенностью этого уравнения является то, что для определения действующих сил не нужно знать существа процессов, происходящих внутри выделенного участка потока жидкости, нужно знать только параметры жидкости на гра-

57

ницах участка. В механике твердого тела известна теорема об изменении количества движения. Она гласит: элементарное изменение количества движения некоторой массы m по какому-либо направлени. равно элементарному импульсу равнодействующей сил, приложенных к этой массе в том же направлении, т.е. d(mñ) = F dt,

где F – проекция равнодействующей всех сил, приложенных к массе m, на какую-либо ось; с – проекция скорости на ту же ось; dt – время действия силы F; F dt – импульс силы; d(mс) – изменение количества движения. Применительно к потокам жидкостей и газов более удобна несколько иная (гидродинамическая) форма теоремы об изменении количества движения.

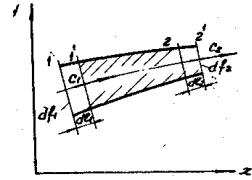
Рис. 4.3. Струйка тока

Рассмотрим установившееся движение элементарной струйки жидкости (рис. 4.3). Проведем два нормальных к ее оси сечения 1 и 2 и обозначим массу жидкости, заключенную в объеме 1–2, через m1–2. За время dt выделенная масса газа переместится в положение 1'–2'. Изменение количества движения выделенной массы жидкости за dt будет определяться только разностью количества движения в элементарных объемах 2–2' и 1–1′, так как при установившемся движении масса жидкости в замкнутом объеме 1′–2 остается неизменной.

В случае неустановившегося движения количество движения

заштрихованного объема 1′–2 с течением времени изменяется.

58

В пределах элементарных объемов 2–2′ и 1–1' параметры равны соответственно:

с1–1′ = с1; с2–2′ = с2; m1-1′ = m2–2′ = m;

поэтому d(mc) = m(c2 – c1), тогда имеем, что m(c2 – c1) = Fdt или, разделив уравнение на dt, получим

При выводе уравнения (4.4) предполагалось, что F, с2, с1 имеют одинаковое направление. В проекциях на оси координат Oх и Oу уравнение (4.4) примет вид:

где G – массовый расход жидкости через площадь сечения струйки, перпендикулярную к направлению скорости; Fx, Fy – соответствующие проекции на оси координат равнодействующей всех внешних сил, приложенных к струйке жидкости на участке 1–2.

Из уравнений (4.5) следует, что проекция равнодействующей всех сил, приложенных к рассматриваемой массе жидкости, на некоторое направление равна секундному изменению количества движения ( G c) этой массы жидкости в том же направлении. Эта теорема известна под названием теоремы Эйлера об изменении количества движения и предложена им в 1754 году. В общем случае внешними силами, приложенными к жидкости на рассматриваемом участке, являются поверхностные нормальные (силы давления, действующие в пределах замкнутого контура между сечениями 1 и 2); поверхностные касательные (силы трения, действующие в направлении, противоположном движению потока); массовые (силы тяжести).

59

Теорема Эйлера может быть распространена и на случай, когда внутри потока жидкости имеется твердое тело или жидкость ограничена поверхностью твердой стенки. Тогда необходимо учитывать, кроме перечисленных сил, еще силы воздействия на жидкость поверхностей твердых стенок, охватывающих поток или находящихся внутри его. В зависимости от конкретных условий задачи тот или иной вид сил может исключаться. Например, в случае применения уравнения Эйлера к движению идеальной жидкости силы трения исключаются; в случае движения жидкости в прямолинейном канале постоянного сечения проекция на ось канала равнодействующей сил давления на боковую поверхность канала равна 0.

4.4. Уравнение момента количества движения

Уравнение момента количества движения не является новым независимым уравнением гидрогазодинамики. Оно представляет новую форму уравнения движения, членами которого являются не силы и не количество движения, а моменты сил и моменты количества движения. Это уравнение широко используется при исследовании вращательного движения жидкости, является основным в теории турбомашин.

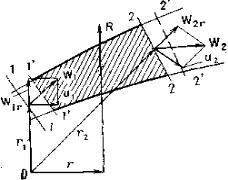
Рис. 4.4. Вывод уравнения момента количества движения

60