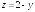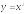- •Содержание Двойной и тройной интегралы.
- •1 Двойной интеграл. Объем цилиндрического тела.
- •2 Свойства двойных интегралов
- •3 Вычисление двойного интеграла
- •4 Двойной интеграл в полярных координатах
- •5 Вычисление площади поверхности
- •6 Вычисление площадей и объёмов посредством двойного интеграла
- •7. Тройной интеграл
- •8. Физические приложения двойных и тройных интегралов
- •Криволинейные интегралы первого и второго рода.
- •1 Криволинейный интеграл второго рода по координатам
- •2 Вычисление криволинейного интеграла по координатам
- •3 Криволинейный интеграл первого рода (по длине дуги)
- •4 Основные свойства криволинейного интеграла первого рода
- •5. Формула Грина.
- •7 Поверхностные интегралы
- •8 Вычисление поверхностного интеграла
- •9 Формула Стокса
- •Элементы теории поля.
- •1 Скалярное поле. Производная по направлению. Градиент
- •2 Векторное поле. Поток и дивергенция поля
- •3 Циркуляция и ротор векторного поля
- •4. Оператор Гамильтона и его применение.
- •Дифференциальные уравнения
- •1. Основные понятия. Дифференциальные уравнения с разделяющимися переменными.
- •2. Однородные уравнения
- •5. Интегрирование дифференциальных уравнений высших порядков.
- •6. Составление дифференциального уравнения по заданной фундаментальной системе решений.
- •7. Линейные неоднородные уравнения с постоянными коэффициентами. Метод подбора.
- •8. Уравнение Эйлера
- •9. Линейные системы дифференциальных уравнений с постоянными коэффициентами
- •Теория функций комплексного переменного.
- •1. Комплексные числа
- •2. Непрерывные функции комплексного переменного
- •3. Дифференцирование функций. Условие Коши-Римана.
- •4 Сопряжённые гармонические функции
- •5 Конформное отображение
- •6 Постоянство растяжений
- •7 Интеграл по комплексному переменному
- •8 Ряд Лорана
- •9 Классификация изолированных особых точек
- •10 Вычеты
- •11. Вычисление интегралов при помощи вычетов
- •12. Вычисление интегралов, содержащих показательную функцию
- •13. Задачи по Теории Функции Комплексного Переменного
3 Вычисление двойного интеграла

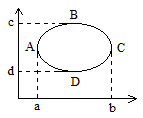 ABC-
ABC-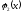 ADC-
ADC- BAD-
BAD- BCD-
BCD-
Теорема
Двойной интеграл по правильной области D равен двукратному (повторному) интегралу по той же области D.

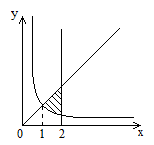
Пример 1
 D:
x
= 2; y
= x;
D:
x
= 2; y
= x;

4 Двойной интеграл в полярных координатах
Пусть
в полярной системе координат
 задана такая областьD,
что каждый луч, проходящий через
внутреннюю точку области D,
пересекает границу области D
не более чем в двух точках (правильная
область).
задана такая областьD,
что каждый луч, проходящий через
внутреннюю точку области D,
пересекает границу области D
не более чем в двух точках (правильная
область).
Предположим,
что D
ограничена кривыми
 ,
, и лучами
и лучами и
и ;
; ;
; ;
; .
.


Разобьём
область D
каким-либо способом на площадки

 .
.
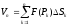 (1)
(1)
 - некоторая точка
на площадке
- некоторая точка
на площадке

Из
теоремы о существовании следует, что
при стремлении наибольшего диаметра
 к нулю, существует предел интегральной
суммы (1).
к нулю, существует предел интегральной
суммы (1).
 (2)
(2)
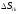




Площадки
 будут трёх видов:
будут трёх видов:
не пересекаемые границей, лежащие в области D;
не пересекаемые границей, лежащие вне области D;
пересекаемые границей области D.
 - произвольная
точка площади
- произвольная
точка площади
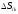

Двойной знак суммирования следует понимать в том смысле, что мы производим сначала суммирование по индексу i, считая k = const, т.е. отбираем слагаемые заключённые между двумя соседними лучами. Внешний знак суммирования означает, что мы собираем вместе все суммы, полученные при первом суммировании.
Найдём
выражение
 .
Она должна быть равна разности площадей
двух секторов.
.
Она должна быть равна разности площадей
двух секторов.


Таким
образом
 .
.
Подынтегральная
сумма будет иметь вид

 - точка площадки
- точка площадки
 .
.
Вынесем
множитель
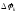 за знак внутренней суммы, потому что он
является общим множителем для всех
слагаемых этой суммы.
за знак внутренней суммы, потому что он
является общим множителем для всех
слагаемых этой суммы.

Предположим,
что
 ,
а
,
а остаётся постоянным, тогда выражение
в квадратных скобках будет стремиться
к
остаётся постоянным, тогда выражение
в квадратных скобках будет стремиться
к

 (3)
(3)



Пример

D: кольцо







5 Вычисление площади поверхности
Пусть
требуется вычислить площадь поверхности
ограниченной линией
 .
Поверхность задана уравнением
.
Поверхность задана уравнением где
где непрерывна и имеет непрерывные частные
производные.
непрерывна и имеет непрерывные частные
производные.



Обозначим
проекцию линии
 на плоскостиOXY
через L.
Область на плоскости OXY,
ограниченную линией L
обозначим D.
Разобьём произвольным образом D
на n
элементарных площадок
на плоскостиOXY
через L.
Область на плоскости OXY,
ограниченную линией L
обозначим D.
Разобьём произвольным образом D
на n
элементарных площадок
 .
В каждой площадке возьмём точку
.
В каждой площадке возьмём точку .
Точке
.
Точке будет соответствовать на поверхности
точка
будет соответствовать на поверхности
точка .
Через точку
.
Через точку проведём касательную плоскость к
поверхности. Её уравнение имеет вид
проведём касательную плоскость к
поверхности. Её уравнение имеет вид (1)
(1)
На
этой плоскости выделим такую площадку
 ,
которая проектируется наOXY
в виде площадки
,
которая проектируется наOXY
в виде площадки
 .
Рассмотрим сумму всех площадок
.
Рассмотрим сумму всех площадок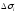 .
Предел
.
Предел этой суммы, когда наибольший из диаметров
площадок
этой суммы, когда наибольший из диаметров
площадок стремится к нулю будем называть площадью
поверхности.
стремится к нулю будем называть площадью
поверхности.
 (2)
(2)
Займёмся
вычислением площади поверхности.
Обозначим через
 угол между касательной плоскостью иOXY.
угол между касательной плоскостью иOXY.

 (3)
(3)



Согласно
определению предел интегральной суммы,
стоящей в правой части последнего
равенства
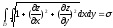
Если
 или
или ,
то соответствующие формулы для вычисления
площади поверхности имеют вид
,
то соответствующие формулы для вычисления
площади поверхности имеют вид


6 Вычисление площадей и объёмов посредством двойного интеграла

Пусть
 неотрицательная непрерывная функция
в замкнутой областиD.
Если объём тела ограниченного сверху
поверхностью
неотрицательная непрерывная функция
в замкнутой областиD.
Если объём тела ограниченного сверху
поверхностью
 ,
снизу областьюD,
а сбоку соответствующей цилиндрической
поверхностью с образующими параллельными
оси OZ
и направляющей совпадающей с границей
области D,
то
,
снизу областьюD,
а сбоку соответствующей цилиндрической
поверхностью с образующими параллельными
оси OZ
и направляющей совпадающей с границей
области D,
то

Пусть тело ограниченное сверху поверхностью
 ,
снизу
,
снизу ,
причём проекцией обеих поверхностей
наOXY
служит область D,
в которой
,
причём проекцией обеих поверхностей
наOXY
служит область D,
в которой
 и
и непрерывны, причём
непрерывны, причём

Пример 1
Вычислить
площадь фигуры ограниченной
 и
и


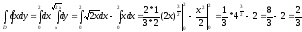

Пример 2
V: z = 0